Тема 7. Дифференциальные уравнения
Дифференциальные уравнения первого порядка. Теорема существования и единственности. Уравнения с разделяющимися переменными. Линейные уравнения первого порядка. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами (случай простых корней и кратных корней). Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Линейные системы с постоянными коэффициентами.
Основные термины: бесконечно убывающая геометрическая прогрессия, положительный ряд, знакопеременный ряд, абсолютная сходимость, условная сходимость знакопеременного ряда, функциональный ряд, степенной ряд, интервал сходимости, центр сходимости, радиус сходимости степенного ряда
Контрольные вопросы по теме 7:
1. Решить уравнения с разделяющимися переменными:
а) 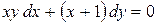 ; б)
; б)  .
.
2. Найти решение уравнения, удовлетворяющее начальным условиям:
а) 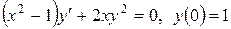 ; б)
; б) 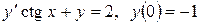 .
.
3. Решить линейное уравнение первого порядка:
а) 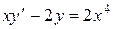 ; б)
; б) 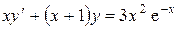 .
.
4. Решить уравнение:
а) 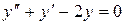 ; б)
; б)  ;
;
в) 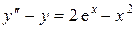 ; г)
; г) 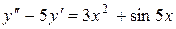 .
.
5. Найти решение уравнения, удовлетворяющее указанным начальным условиям:
а) 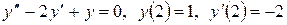 ;
;
б) 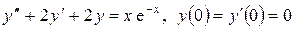 .
.
6. Решить систему дифференциальных уравнений:
а) 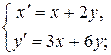 б)
б) 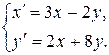
ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ
Практическое занятие 1 по теме «Предел и непрерывность функции»
План:
1. Рассмотрение понятия предела последовательности.
2. Рассмотрение понятий предела и непрерывности функции.
2. Решение задач.
Контрольные вопросы и задачи
1. Найдите предел последовательности
1.1. 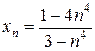 . 1.2.
. 1.2. 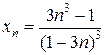 .
.
1.3. = 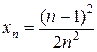 . 1.4.
. 1.4. 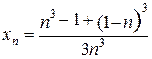 .
.
1.5. 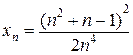 . 1 .6.
. 1 .6. 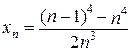 .
.
1.7. 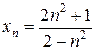 . 1.8.
. 1.8. 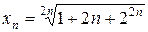 .
.
1.9. 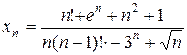 . 1.10.
. 1.10. 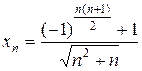 .
.
1.11. 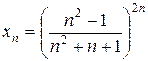 . 1.12.
. 1.12. 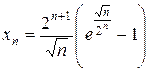 .
.
2. Найдите предел функции
2.1. 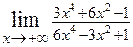 . 2.2.
. 2.2. 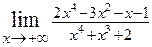 . 2.3.
. 2.3. 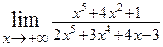 .
.
2.4. 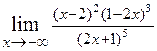 . 2.5.
. 2.5. 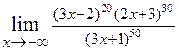 . 2.6.
. 2.6. 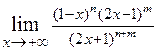 . 2.7.
. 2.7. 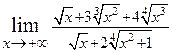 . 2.8.
. 2.8. 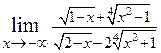 . 2.9.
. 2.9. 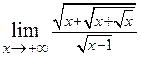 .
.
2.10. 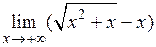 . 2.11.
. 2.11. 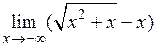 .
.
2.12. 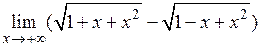 . 2.13.
. 2.13. 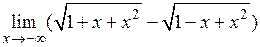 .
.
2.14.  . 2.15.
. 2.15. 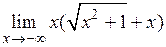 .
.
2.16. 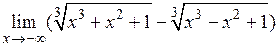 .
.
2.17. 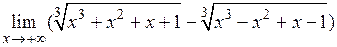 .
.
2.18. 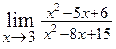 . 2.19.
. 2.19. 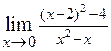 . 2.20.
. 2.20. 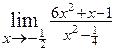 .
.
2.21. 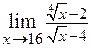 . 2.22.
. 2.22. 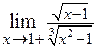 . 2.23.
. 2.23. 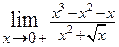 .
.
2.24. 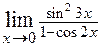 . 2.25.
. 2.25.  . 2.26.
. 2.26. 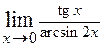 .
.
2.27. 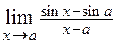 . 2.28.
. 2.28. 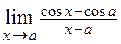 . 2.29.
. 2.29. 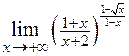 .
.
2.30. 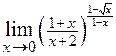 . 2.31.
. 2.31. 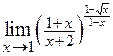 . 2.32.
. 2.32. 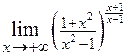 .
.
2.33. 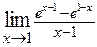 . 2.34.
. 2.34. 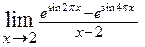 . 2.35.
. 2.35. 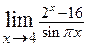 .
.
2.36. 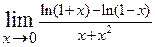 . 2.37.
. 2.37. 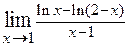 . 2.38.
. 2.38. 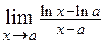 .
.
3. Следующие функции исследуйте на непрерывность. Укажите тип точек разрыва. Выясните, являются ли функции непрерывными справа или слева в точках разрыва
3.1. 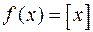 . 3.2.
. 3.2. 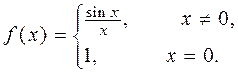
3.3. 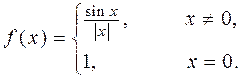 3.4.
3.4. 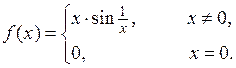
3.5. 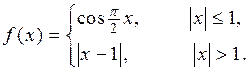 3.6.
3.6. 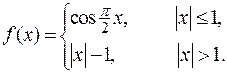
Литература
Основная:
1. Баврин И.И. Математика для гуманитариев: учебник для студентов учреждений высш. Проф. образования гуманитарных направлений. М.: Изд. центр «Академия», 2011. С. 42–73.
2. Высшая математика для экономистов / Под ред. Н.Ш. Кремера. М.: ЮНИТИ, 2002. С. 141–175.
3. Ильин В.А., Куркина А.В. Высшая математика: учеб. М.: Проспект, 2009. С. 146–225.
4. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М, 1997. С. 61–65.
5. Красс М.С. Математика для экономических специальностей: Учебник. М.: ИНФРА-М, 1999. С. 22–74.
6. Пехлецкий И.Д. Математика: Учеб. для студ. образоват. учреждений сред. проф. образования. М.: Издательский центр «Академия», 2003. С. 45–58.
Дополнительная:
1. Ганичева А.В. Краткий курс математического анализа: Учебное пособие. Тверь, 2002. С. 12–32.
2. Данчул А.Н., Митини А.И., Сафонова Т.Е., Симонов В.А. Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика. Учебно-методическое пособие / Под ред. А.Н.Данчула. М., 2004. С. 5–13.
3. Кремер Н.Ш. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. Пособие. М.: Издательство Юрайт; ИД Юрайт, 2011. С. 145–158.
4. Луканкин Г.Л., Луканкин А.Г. Высшая математика для экономистов: курс лекций: учебное пособие для вузов. М.: Издательство «Экзамен», 2006. С. 79–105.
5. Практикум по математике: пособие для студентов 1 курса / сост. А.Л.Кириллов, В.И.Клоков, С.В.Полянская. Спб.: Изд-во СЗАГС, 2009. С. 4–8.
6. Сборник задач по высшей математике для экономистов: Учебное пособие/ Под ред. В.И. Ермакова. М.: ИНФРА-М, 2004. С. 142–148.
7. Щипачёв В.С. Высшая математика. Базовый курс: учебное пособие/ под ред. акад. А.Н. Тихонова. М.: Издательство Юрайт; ИД Юрайт, 2011. С. 102–222.
Практическое занятие 2 по теме «Дифференциальное исчисление функций одной переменной»
План:
1. Нахождение производной первого порядка.
2. Касательная и нормаль.
3. Производные высших порядков.
4. Решение задач.
Контрольные вопросы и задачи
1. Найдите производную функции 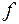 .
.
1.1. 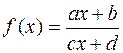 . 1 .2.
. 1 .2. 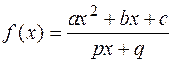 .
.
1.3.  . 1.4.
. 1.4. 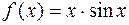 .
.
1.5. 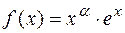 . 1.6.
. 1.6. 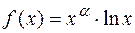 .
.
1.7. 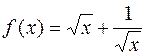 . 1.8.
. 1.8. 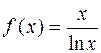 .
.
1.9. 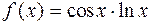 . 1.10.
. 1.10. 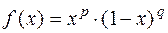 .
.
1.11. 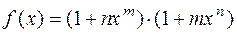 . 1.12.
. 1.12. 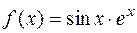 .
.
1.13. 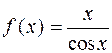 . 1.14.
. 1.14. 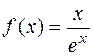 . 1.15.
. 1.15. 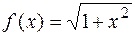 .
.
1.16. 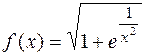 . 1.17.
. 1.17. 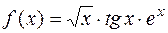 .
.
1.18. 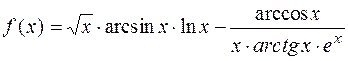 .
.
1.19. 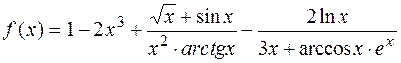 .
.
1.20. 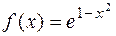 . 1.21.
. 1.21. 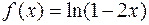 . 1.22.
. 1.22. 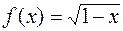 .
.
1.23. 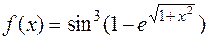 . 1.24.
. 1.24. 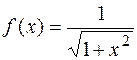 .
.
1.25. 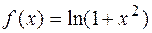 . 1.26
. 1.26 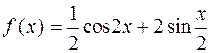 .
.
1.27. 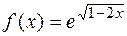 . 1.29.
. 1.29. 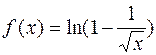 .
.
2. Найдите уравнения касательной и нормали к функции 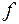 в точке
в точке 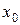 .
.
2.1. 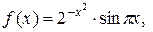 a)
a) 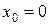 ; б)
; б) 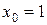 .
.
2.2. 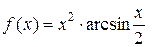 , a)
, a) 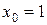 ; б)
; б) 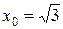 .
.
2.3. 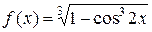 , а)
, а) 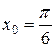 ; б)
; б) 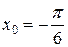 .
.
2.4.  , a)
, a) 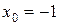 ; б)
; б) 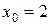 .
.
3. Найдите производные указанного порядка n функции 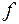 .
.
3.1. 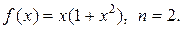 3.2.
3.2. 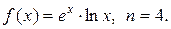
3.3. 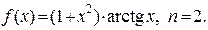 3.4.
3.4. 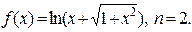
3.5. 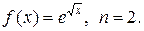 3.6.
3.6. 
3.7. 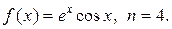 3.8.
3.8. 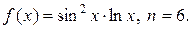
Литература
Основная:
1. Баврин И.И. Математика для гуманитариев: учебник для студентов учреждений высш. Проф. образования гуманитарных направлений. М.: Изд. центр «Академия», 2011. С. 80–117.
2. Высшая математика для экономистов / Под ред. Н.Ш. Кремера. М.: ЮНИТИ, 2002. С. 176–250.
3. Ильин В.А., Куркина А.В. Высшая математика: учеб. М.: Проспект, 2009. С. 226–291.
4. Колесников А.Н. Краткий курс математики для экономистов: Учебное пособие. М.: ИНФРА-М, 1997. С. 66–117.
5. Красс М.С. Математика для экономических специальностей: Учебник. М.: ИНФРА-М, 1999. С. 81–133.
6. Пехлецкий И.Д. Математика: Учеб. для студ. образоват. учреждений сред. проф. образования. М.: Издательский центр «Академия», 2003. С. 131–145.
Дополнительная:
1. Ганичева А.В. Краткий курс математического анализа: Учебное пособие. Тверь, 2002. С. 33–58.
2. Данчул А.Н., Митини А.И., Сафонова Т.Е., Симонов В.А. Математика: Математический анализ. Дифференциальные уравнения. Теория вероятностей. Математическая статистика. Учебно-методическое пособие / Под ред. А.Н.Данчула. М., 2004. С. 14–27.
3. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: Учебник. М.: МГУ им. М.В.Ломоносова, Издательство «ДИС», 1998. С. 42–55.
4. Кремер Н.Ш. Математика для экономистов: от Арифметики до Эконометрики: учеб.-справоч. Пособие. М.: Издательство Юрайт; ИД Юрайт, 2011. С. 159–182.
5. Луканкин Г.Л., Луканкин А.Г. Высшая математика для экономистов: курс лекций: учебное пособие для вузов. М.: Издательство «Экзамен», 2006. С. 106–159.
6. Практикум по математике: пособие для студентов 1 курса / сост. А.Л.Кириллов, В.И.Клоков, С.В.Полянская. Спб.: Изд-во СЗАГС, 2009. С. 9–14.
7. Сборник задач по высшей математике для экономистов: Учебное пособие/ Под ред. В.И. Ермакова. М.: ИНФРА-М, 2004. С. 149–178.
8. Щипачёв В.С. Высшая математика. Базовый курс: учебное пособие/ под ред. акад. А.Н. Тихонова. М.: Издательство Юрайт; ИД Юрайт, 2011. С. 223–313.
