Метод Ньютона–Рафсона

Чтобы обеспечить сходимость метода от выбранного начального приближения 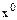, применяется модификация, называемая методом Ньютона–Рафсона. Вычисление (k+1)-го приближения в этой модификации осуществляется по правилу

,

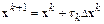где 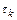– параметр, значение которого на k-й итерации выбирается из условия

.

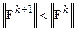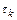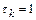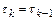Стратегия выбора параметра на итерации может быть такой. Вначале принимается пробное значение либо и далее это значение видоизменяется до выполнения сформулированного условия. Это условие может потребовать многократного вычисления вектора 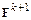на текущей итерации. Очевидно, что при 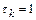метод Ньютона–Рафсона совпадает с методом Ньютона.

Методы продолжения по параметру.

Эти методы позволяют обеспечить сходимость метода Ньютона от выбранного начального приближения 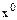.Сущность методов продолжения по параметру заключается в замене исходной задачи последовательностью задач, каждая последующая задача при этом незначительно отличается от предыдущей. Последовательность строится таким образом, что первая система имеет решение 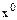, а последняя система совпадает с исходной задачей. Поскольку системы отличаются незначительно, то решение предыдущей задачи окажется хорошим начальным приближением для последующей. Решая такую последовательность задач методом Ньютона, получим в итоге решение исходной системы. Рассмотрим способ построения указанной последовательности задач.

Пусть при решении системы

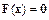
используется начальное приближение 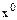. Заменим исходное уравнение 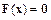уравнением с параметром

,

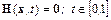которое при 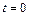имеет решение 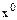, а при 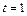совпадает с решением исходной задачи, т. е.

.

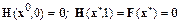В качестве 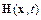можно выбрать функции

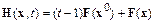
либо

.

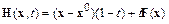Разобьем отрезок 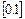точками 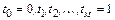на 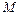интервалов. Получим искомую последовательность систем:

.

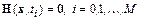Метод Ньютона для плохо обусловленных задач.

Если матрица Якоби 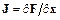плохо обусловлена, погрешность решения линейной системы

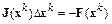
может оказаться значительной из-за ошибок округления. Поэтому в

случае плохо обусловленных матриц 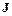при вычислении вектора поправок 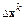привлекают систему

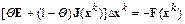
с числовым параметром 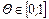, где E–единичная матрица. При 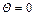модифицированная система совпадает с линейной системой стандартного метода Ньютона, при стремлении 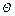к единице число обусловленности модифицированной системы также стремится к единице. Однако скорость сходимости соответствующего метода значительно ухудшается, поскольку при 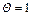метод вырождается в метод простых итераций.