Адаптивные методы прогнозирования
Адаптивные методы позволяют строить описание процессов с учетом различной ценности членов динамического ряда, при этом влияние более поздних членов динамического ряда на дальнейшее развитие процесса учитывается с большим весом, чем более ранних. В связи с этим, появляется возможность более оперативно реагировать на изменяющуюся обстановку и давать на ближайшую перспективу более точные прогнозы.
Наиболее известным и рациональным адаптивным методом является метод гармонических весов. Для осуществления прогноза методом гармонических весов исходный динамический ряд разбивается на фазы (части). Рассмотрим процедуру прогнозирования данным методом на примере из параграфа 2.2.1.:
Год Номер п/п, 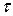 Объем продаж
Объем продаж

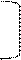
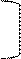 2001 1 1280 I – фаза
2001 1 1280 I – фаза 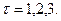

 2002 2 1350 II – фаза
2002 2 1350 II – фаза 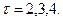
 2003 3 1480 III – фаза
2003 3 1480 III – фаза 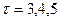 .
.
2004 4 1550
2005 5 1660
Каждую фазу аппроксимируем линейной функцией 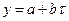 . Для первой фазы функция имеет вид:
. Для первой фазы функция имеет вид:
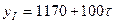 ,
,
для второй 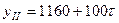 ,
,
для третьей 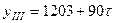 .
.
При 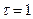 имеем:
имеем:
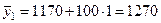 .
.
При 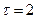 :
:
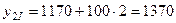 ,
, 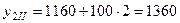 ,
,
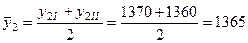 .
.
При 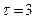 :
:
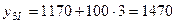 ,
, 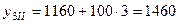 ,
, 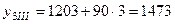 .
.
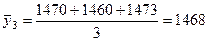 .
.
При 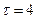 :
:
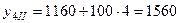 ,
, 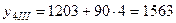 .
.
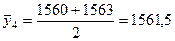 .
.
При 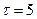 :
:
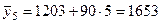 .
.
Рассчитаем приросты по формуле:
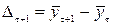 .
.
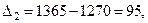
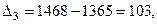
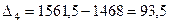 ,
, 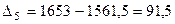 .
.
Рассчитаем гармонические веса. Если самая ранняя информация имеет вес: 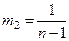 , то вес информации, относящийся к следующему моменту времени, равен:
, то вес информации, относящийся к следующему моменту времени, равен:
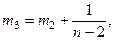 т.е.
т.е. 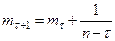 .
.
Для нашего примера:
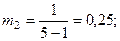
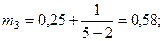
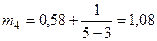 ;
; 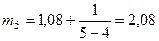 .
.
Чтобы получить гармонические коэффициенты, удовлетворяющие условию 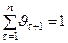 , необходимо гармонические веса разделить на
, необходимо гармонические веса разделить на 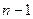 :
:
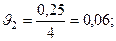
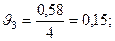
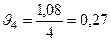 ;
; 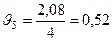 .
.
Средний прирост:
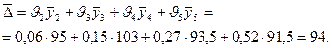
Прогноз на 2006 год: 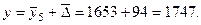
Чтобы избежать столь сложных расчетов часто весовые коэффициенты назначаются экспертным путём, например: 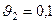 ;
; 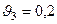 ;
; 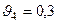 ;
; 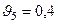 . Приросты рассчитываются по формуле:
. Приросты рассчитываются по формуле: 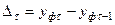 . В нашем примере:
. В нашем примере:
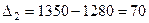 ;
;
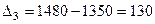 ;
;
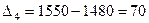 ;
;
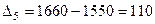 .
.
Средний прирост:
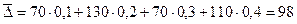 .
.
Прогноз на 2006 год: 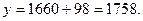
Методы моделирования
В настоящее время моделирование считается наиболее эффективным методом прогнозирования. Алгоритм построения экономико-математической модели включает следующие этапы:
1. формулировка цели прогнозного исследования;
2. выделение в объекте прогнозирования структурных элементов, оказывающих влияние на характер и динамику его развития;
3. выявление внешних факторов, влияющих на развитие объекта прогнозирования;
4. логическое описание взаимосвязей между элементами объекта прогнозирования, внешними и результирующими факторами (построение информационной модели);
5. формализация (математическое описание) взаимосвязей между элементами объекта прогнозирования, внешними и результирующими факторами (показателями);
6. проведение расчетов, корректировка и уточнение модели.
Экономико-математические модели имеют следующие преимущества:
- возможность отражения многосторонних связей между результирующими и влияющими факторами;
- возможность использования экономико-математических моделей при управлении экономическими процессами и при поиске наиболее эффективных (оптимальных) управленческих решений.
В соответствии с математической формой построения выделяют следующие типы экономико-математических моделей:
- экономико-статистические;
- структурные;
- оптимизационные;
- имитационные и др.
