Метод множителей Лагранжа
Пусть задана задача линейного программирования
L = f (M ) = (x1 ; x2 ;...xn )® max(min)
при ограничениях:
gi(x1, x2,...xn) = 0,i = 1,1m.
Пусть функции
f (x1, x2,...xn) и
g(x1 , x2,...xn)
непрерывны вместе со своими
частными производными. Так как ограничения заданы в виде уравнений, то для решения задачи воспользуемся методом отыскивания условного экстремума функ- ции нескольких переменных, который сводится к исследованию на обычный экс- тремум функции Лагранжа.
L(x1, x2,...xn , l1,..., lm) =
m
f (x1, x2,...xn )+ ålkgk(x1, x2,...xn ),
k =1
где
l (k = 1m) - множители Лагранжа.
|
|
ï = 0, (i = 1m),
ì¶LM
¶x
í i
|
|
(12)
из которых могут быть найдены неизвестные где
M (x0, x0,..., x0) - точка, в которой
возможен условный экстремум.
0 1 2 n
Достаточные условия наличия условного экстремума связана с изучением знака 2-го дифференциала функции Лагранжа:
d 2 L(x0 , x0,..., x0, l0,..., l0 , dx ,..., dx )
1 2 n 1 m 1 n
для каждого набора значений
x0,..., x0, l0,...l0, полученный из системы (12) при
2 n 1 m
условии , что
dx1,..., dxn
удовлетворяет уравнениям:
n
å
g =1
¶gk(M 0 )
¶x j
dx j
= 0, k
= 1, m
(12)
dx2+ dx2+ ... + dx2¹ 0.
1 2 n
Функция
L = f (M )
имеет условный максимум в точке М0, если для всевоз-
можных значений
венство:
dx1,..., dxn, удовлетворяющих условиям (12), выполняется нера-
d 2 L(x0 , x0,..., x0, l0,..., l0, dx ,..., dx
)< 0
1 2 n 1 m 1 n
и условный минимум, если при этих условиях:
d 2 L(x0 , x0,..., x0, l0,..., l0, dx ,..., dx
)> 0
1 2 n 1 m 1 n
В случае двух переменных при одном ограничении гранжа имеет вид:
g(x; y) = 0 , то функция Ла-
L(x; y;l) =
f (x; y)+ lg(x; y).
Система для нахождения стационарных (критических) точек состоит из трех уравнений:
¶L= 0, ¶L= 0, g(x; y) = 0.
¶x
Если
¶y
M (x0 , y0, l0)
- любой из решений этой системы, вместо изучения знака
второго дифференциала, можно исследовать знак определителя D.
0
D = - g ¢x (M 0 )
g ¢y (M 0 )
При этом:
g ¢x (M 0 ) Lx¢¢x (M 0 ) Lx¢¢y (M 0 )
g ¢y (M 0 ) Lx¢¢y (M 0 ). L¢y¢y (M 0 )
1) если
2) если
D < 0 , то функция
D > 0 , то функция
Z = f (x; y) имеет в точке
Z = f (x; y) имеет в точке
M 0 условный максимум,
M 0 условный минимум.
Объясним идею метода на примере задачи нелинейного программирования, зависящей от двух переменных.
f(x1, х2)→max
g( x l , x 2 ) = b
На плоскости x10x2уравнение g( xx, x 2 )= b определяет график некоторой функции, представленный на рис. 26. На нем показаны несколько линий уровня некоторой функции f(х 1гх 2 ) и выбранное в качестве примера направление ее воз- растания.
f(x1,x2)=C
x2
l k
A
f(x1,x2)=C3
f(x1,x2)=C2
f(x1,x2)=C1
g(x1,x2)=b
Направление возрастания функции
0 x1
рис. 26
В точке А, в которой функция f достигает максимального значения, совпада- ют касательные линии к графикам функций
f(х1,х2) = С и g( x l , x 2 )= b .
Следовательно, в точке А векторы-нормали к функциям g( x l , x 2 )= b и f ( x 1 , x 2 )= C пропорциональны. Обозначим эти векторы соответственно через k и l. Получаем l = λ k,где λ - некоторый коэффициент пропорциональности. Координа- тами векторов l и k являются значения частных производных функций f и g соот- ветственно в точке А.
l =( дf/дx 1 ; дf/дx 2 );
k =( дg/дx 1 ; дg/дx 2 ).
Из условия пропорциональности в точке А имеем
дf/дx 1 = λ*дg/дx 2 ; дf/дx 2 = λ*дg/дx 2 .
Для определения значений х 1 ,х 2 , в которых функция f достигает максимума,
к этим уравнениям надо добавить условие принадлежности точки А графику функ- ции g( x 1 , х 2 ) = b.
Окончательно получаем систему уравнений, определяющую оптимальное
решение поставленной задачи
дf/ дx 1 = λ* дg/ дx 1 дf/ дx 2 = λ* дg/ дx 2 g( x 1 , х 2 )= b
Введем новую функцию
F( x 1 ,х 2 , λ) = f ( x 1 ,х 2 ) + λ ( b- g( x 1 ,х 2 ) ) .
Тогда последняя система перепишется в виде
д F( x 1 , x 2 , λ)/ дx 1 = дf( x 1 , x 2 ) / дx 1 - λ* д( x 1 , x 2 ) / дx 1 =0 д F( x 1 , x 2 , λ)/ дx 2 = дf( x 1 , x 2 ) / дx 2 - λ* д( x 1 , x 2 ) / дx 2 =0 д F/ дλ= b- g( x 1 , x 2 )= 0
Функцию F и называют функцией Лагранжа.
Задача 4.1. Найти условный экстремум функции
Z = x + 2 y
при условии
x2 + y 2 = 5
методом Лагранжа.
Решение.
Для нашей задачи составляем функцию Лагранжа:
L(x; y;l) = x + 2y + l(x2 + y 2 = 5).
Находим частные производные:
¶L= 1 + lx; ¶L= 2 + 2ly.
¶x ¶y
Система уравнений принимает вид:
ì1 + 2lx = 0,
ï
í1 + ly = 0,
|
= 5.
Решаем систему:
ì 1
ïx = - 2l ,
ï
ï 1
í y = - ,
ï 2
ï 1
1 2 1
|
= 5, Þ l = ,
|
ï
íx1= -1,
ìl2= - 12,
|
íx2= 1,
M1 (-1,-2);
ï y = -2,
ï y = 2,
M 2 (1,2).
îï 1
îï 2
Далее находим вторые частные производные функции Лагранжа и составля-
ем второй дифференциал
d 2 L :
Lx¢¢x
= 2l; Lx¢¢y
= 0; L¢y¢x
= 0; L¢y¢y
= 2l.
Следовательно
d 2 L = 2l(dx2 + dy 2 )
При
l2= 12
d 2 L > 0 , следовательно, в точке
M1 (-1;-2)
функция имеет услов-
ный минимум, равный:
Zmin (M1) = -5.
При
l2 = - 12
d 2 L > 0 , следовательно, в точке
M 2 (1;2)
функция имеет макси-
мум, равный:
Zmax(M 2 ) = 5
Теперь определить тип экстремумов в стационарных точках другим способом (с помощью определителя D ):
|
= 2x;
При
l = 1
g¢y = 2 y; Lx¢¢x
= 2l; Lx¢¢y
= 0; L¢y¢x
= 0; L¢y¢y
= 2l.
0
D1 = - 2
- 4
- 2 - 4
1 0
0 1
= 20 > 0
следовательно, в точке
M1 (-1;-2)
для
l = 12
функция
Z = x + 2 y
имеет услов-
ный минимум, равный
Zmin (M1) = -5;
При
l = - 1
2
0
D 2 = 2
2 4
-1 0 = -20 < 0
0 1
следовательно, в точке
M 2 (1;2)
для
l = - 12
функция имеет условный макси-
мум, равный
Zmax(M 2 ) = 5.
Задача 4.2. Применяя метод Лагранжа, найти точки условного экстремума
функции U = xy + yz
при заданных ограничениях:
ìx 2 + y 2 = 2,
í
î y + z = 2.
x, y, z -целочисленные координаты. Решение. Составляем функция Лагранжа:
| |
| |
(y + z - 2).
Находим частные производные функции Лагранжа:
Lx¢ = y + 2l1 x;
L¢y = x + z + 2l1 y + l2;
Lz¢ = y + l2 ;
L¢ = x2
|
+ y 2
- 2;
L¢
|
= y + z - 2.
Для нахождения стационарных точек, получаем систему уравнений:
ì
ï
ï y = -l2
(из3)
ì y + 2l1x = 0,
ï
ïx + z + 2l1y + l2= 0,
ï
ï
ïx =
ï
ï
l 2
2l1
(из1,3)
(из5и1)
í y + l2= 0,
íz = 2 - y = 2 + l2
|
= 2,
ï l
| |
- 2l1l2
+ l2= 0
(из2)
ïî y + z = 2;
ï 2l1
ï 2
ï l2
ï 2
| |
(из4)
î 4l1
Можно показать, что из последних уравнений системы следует уравнение
| |
l1:
| |
- 32l1
+ 8l1-1 = 0
Корни этого уравнения:
l (1)= - 1 ;
l (2) = 1 ;
l (3)= 2 -
3; l (4)= 2 + 3.
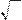
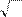1 2 1 2 1 1
а) при значении
l (1)= - 1 ,
получим l
= -1; x = 1; y = 1; z = 1. Стационарная точка
M1 (1;1;1).
1 2 2
б) при значении
l (2)= 1 , получим l
= -1; x = -1; y = 1; z = 1. Стационарная точ-
1 2 2
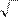ка M1 (-1;1;1).
в) значения
l1= 2 ±
3 является посторонними корнями, им соответствуют
стационарные точки с не целочисленными координатами (не соответствуют усло- вию задачи).
Далее, находим вторые частные производные функции L и составляем второй
дифференциал
d 2 L :
Lx¢¢x
= 2l1;
Lx¢¢y
= 1;
Lx¢¢z
= 0;
L¢y¢x
= 1;
L¢y¢y
= 2l1;
L¢y¢z
= 1;
Lz¢¢x = 0;
Lz¢¢y = 1;
Lz¢¢z = 0.
Следовательно
d 2 L = 2l dx2+ 2dxdy + 2l dy 2 + 2dydz.
1 1
Из условий связи следуют равенства:
ìxdx + ydy= 0,
í
îdy + dx = 0.
Исследуем знак
l1 = -0.5;l 2 = -1; M1 (1;1;1):
Откуда получаем:
d 2 L
для первой стационарной точки при
ìdx+ dy= 0,
í
îdy + dz = 0.
dx = -dy;
dz = -dy Þ d 2 L(M
) = -dy 2 - 2dy 2 - dy2 - 2dy2< 0
| |
Lmax(M1) = 1×1+1×1 = 2.
M1 (1;1;1). функция имеет условный максимум, равный
Исследуем знак
¢ ¢
d 2 L
для второй стационарной точки при
l1 = 0.5; l2
= -1; M 2 (-1;1;1):
ì-dx+ dy= 0,
í Þ
îdy + dz = 0;
dx = dy, dz = -dy.
поэтому
d 2 L(M
) = dy 2 + 2dy 2 + dy 2 - 2dy2= 2dy 2 > 0.
| |
Lmin(M 2 ) = -1×1+1×1 = 0.
M 2 (-1;1;1)
функция имеет условный минимум, равный