Метод сеток. Метод энергетических оценок
На отрезке 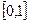 рассмотрим равномерную сетку узлов
рассмотрим равномерную сетку узлов 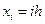 ,
, 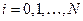 . Пусть
. Пусть 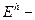 множество сеточных функций, заданных на этой сетке
множество сеточных функций, заданных на этой сетке 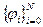 ,
, 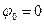 ,
, 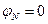 . Для функций из этого множества определим скалярное произведение
. Для функций из этого множества определим скалярное произведение
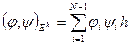 ,
, 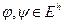 ,
,
и норму
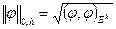 .
.
Тогда 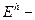 гильбертово пространство.
гильбертово пространство.
Рассмотрим формулы суммирования по частям. Они являются разностными аналогами формул интегрирования по частям. Пусть 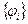 и
и 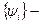 сеточные функции, тогда
сеточные функции, тогда
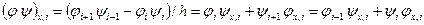 ,
,
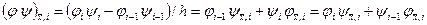 .
.
Эти формулы – суть аналоги формулы дифференцирования произведения
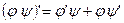 .
.
Из приведенных формул с учетом 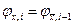 следует, что
следует, что
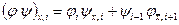 .
.
Просуммируем это соотношение в пределах от 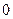 до
до 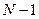 . Получим
. Получим
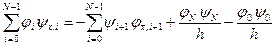 .
.
Или, что то же самое:
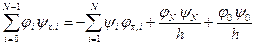 .
.
Для дальнейшего нам будет удобнее переписать это равенство в виде
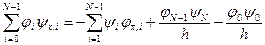 . (1.56)
. (1.56)
Исследование сходимости метода сеток для краевой задачи (1.4), (1.5) методом энергетических оценок начнем с доказательства важного неравенства. Умножим уравнение (1.18) на сеточную функцию 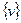 скалярно в
скалярно в 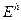 . Получим
. Получим
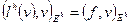 . (1.57)
. (1.57)
Замечание. Здесь принято соглашение, что 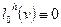 ,
, 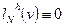 ,
, 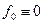 ,
, 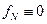 .
.
Преобразуем левую часть (1.57):
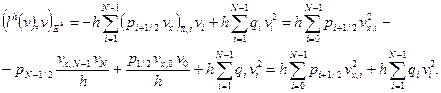 (1.58)
(1.58)
Из равенства (1.58) легко выводится неравенство
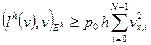 . (1.59)
. (1.59)
Введем в рассмотрение для функций из 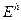 сеточную норму
сеточную норму
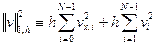 .
.
Эта норма является сеточным аналогом нормы в пространстве 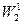 .
.
Покажем теперь, что верен сеточный аналог неравенства (1.22). Заметим, что имеет место равенство
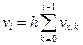 ,
, 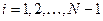 ,
, 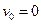 ,
, 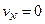 .
.
Возведем обе части этого равенства в квадрат, получим
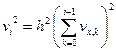 .
.
Воспользуемся неравенством
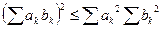 .
.
Тогда
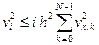 .
.
Отсюда следует, что
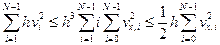 . (1.60)
. (1.60)
и
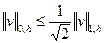 . (1.61)
. (1.61)
Из (1.59) и (1.60) легко выводится неравенство
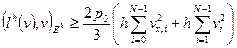 ,
,
которое можно переписать в виде
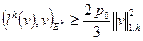 . (1.62)
. (1.62)
Далее:
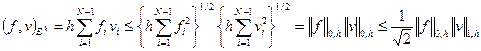 . (1.63)
. (1.63)
Из неравенств (1.62) и (1.63) и из равенства (1.57) получаем
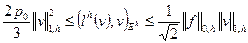 ,
,
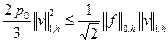 .
.
Откуда, как нетрудно понять,
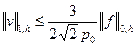 . (1.64)
. (1.64)
Это очень важное неравенство. Из него следует, что при 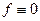 система сеточных уравнений (1.18), (1.19) имеет только тривиальное решение. Тем самым эта система имеет единственное решение при любой правой части.
система сеточных уравнений (1.18), (1.19) имеет только тривиальное решение. Тем самым эта система имеет единственное решение при любой правой части.
Теперь для погрешности 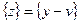 запишем соотношение
запишем соотношение
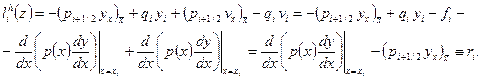
Можно считать, что сеточная функция 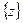 является решением системы сеточных уравнений (1.18), (1.19) с правой частью
является решением системы сеточных уравнений (1.18), (1.19) с правой частью 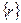 . Тогда для
. Тогда для 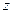 согласно (1.64) справедлива оценка
согласно (1.64) справедлива оценка
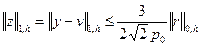 . (1.65)
. (1.65)
Примем во внимание, что
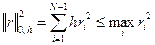 .
.
Оценим теперь 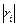 . Воспользуемся для этого разложением
. Воспользуемся для этого разложением 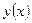 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 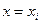 . Тогда, в предположении что
. Тогда, в предположении что 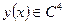 , имеем
, имеем
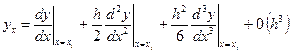 ,
,
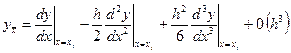 .
.
Учитывая эти формулы, 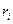 можно представить в виде
можно представить в виде
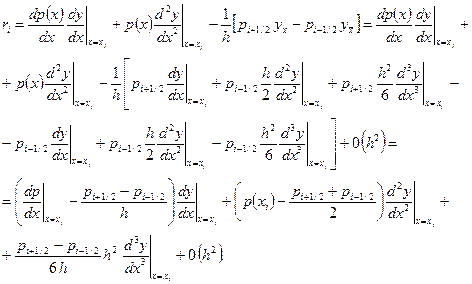
Нетрудно показать, что
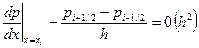 ,
,
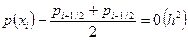 ,
,
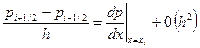 .
.
Для доказательства этих соотношений следует разложить 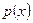 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 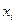 . Доказательство этих утверждений предоставляется читателям.
. Доказательство этих утверждений предоставляется читателям.
В итоге мы получаем, что
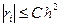
и, следовательно, согласно (1.65)
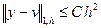 . (1.66)
. (1.66)
Оценка (1.66) получена в предположении, что 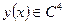 . Оценку (1.66) можно записать иначе:
. Оценку (1.66) можно записать иначе:
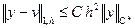 . (1.67)
. (1.67)
