Метод сеток для стационарных задач
В двумерной области 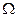 с границей
с границей 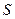 рассмотрим следующую краевую задачу:
рассмотрим следующую краевую задачу:
L 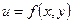 , ,
, , 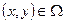 , (2.9)
, (2.9)
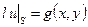 ,
, 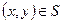 , (2.10)
, (2.10)
где L – линейный эллиптический оператор, более общий, чем оператор Лапласа:
L 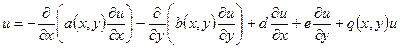 ,
,
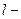 линейный оператор граничного условия.
линейный оператор граничного условия.
Область 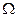 покроем сеткой, образованной прямыми, параллельными осям координат (рис.8).
покроем сеткой, образованной прямыми, параллельными осям координат (рис.8).
На рис.8 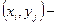 узлы сетки,
узлы сетки, 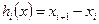 ,
, 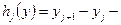 шаги сетки. Если все
шаги сетки. Если все 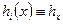 ,
, 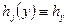 , то сетка называется регулярной или равномерной.
, то сетка называется регулярной или равномерной.
Введем понятие сеточной области. Те узлы сетки, которые лежат внутри области  вместе с четырьмя соседними, назовем внутренними узлами сеточной области. Их совокупность обозначим
вместе с четырьмя соседними, назовем внутренними узлами сеточной области. Их совокупность обозначим  . Те узлы сетки, которые лежат внутри
. Те узлы сетки, которые лежат внутри 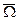 , но для которых один из соседних узлов лежит вне
, но для которых один из соседних узлов лежит вне 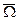 , называют граничными. Их совокупность обозначим через
, называют граничными. Их совокупность обозначим через 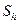 (
( 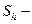 граница сеточной области). Тогда все множество узлов, лежащих в
граница сеточной области). Тогда все множество узлов, лежащих в 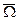 , образует сеточную область
, образует сеточную область 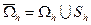 .
.
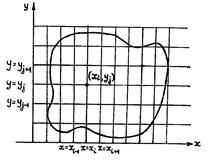
Рис.8. Прямоугольная сетка для области
Такое определение сеточной области не является единственно возможным. Выбор сеточной области определяется еще и тем, какие члены содержит уравнение.
Во внутренних узлах сеточной области 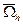 записываются сеточные уравнения, аппроксимирующие дифференциальное уравнение (2.9), а в граничных узлах задаются граничные условия, аппроксимирующие (2.10). Поскольку каждому узлу сетки из
записываются сеточные уравнения, аппроксимирующие дифференциальное уравнение (2.9), а в граничных узлах задаются граничные условия, аппроксимирующие (2.10). Поскольку каждому узлу сетки из 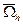 соответствует значение искомой сеточной функции и в каждом внутреннем узле записывается сеточное уравнение, число сеточных уравнений равно числу внутренних узлов, т.е. числу узлов в
соответствует значение искомой сеточной функции и в каждом внутреннем узле записывается сеточное уравнение, число сеточных уравнений равно числу внутренних узлов, т.е. числу узлов в 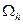 .
.
Пусть сетка равномерная. Выпишем вид сеточного уравнения во внутреннем узле 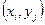
(L 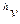 )
) 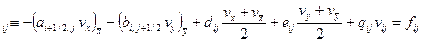 . (2.11)
. (2.11)
Это сеточное уравнение получается, если принять следующие аппроксимации:
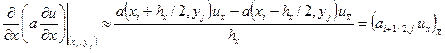 ,
,
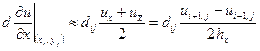 .
.
Соответствующим образом аппроксимируются производные по  .
.
В системе (2.11) число уравнений меньше числа неизвестных, так как в некоторых уравнениях присутствуют значения искомой функции в граничных узлах. Чтобы число уравнений стало равно числу неизвестных, следует использовать аппроксимацию граничных условий.
Рассмотрим случай первого краевого условия
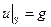 . (2.10)
. (2.10)
 Простейший способ аппроксимации краевого условия (2.10) состоит в сносе граничного условия с границы
Простейший способ аппроксимации краевого условия (2.10) состоит в сносе граничного условия с границы 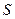 на
на 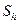 . Обычно это делают так:
. Обычно это делают так:
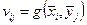 ,
, 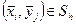 , (2.12)
, (2.12)
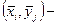 ближайшая к узлу
ближайшая к узлу 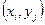 точка на
точка на 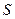 .
.
Таким образом, получена система сеточных уравнений (2.11), (2.12), аппроксимирующая задачу (2.9), (2.10).
Снос граничных условий – это довольно грубый прием аппроксимации граничных условий. Более точным приемом является использование линейной интерполяции. Вместо задания значений 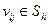 путем сноса значений функции
путем сноса значений функции 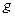 с
с 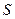 на
на 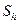 задают значения
задают значения 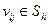 с помощью линейной интерполяции по значениям
с помощью линейной интерполяции по значениям 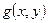 на
на 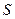 и искомого решения во внутреннем узле. Поясним ситуацию на примере (рис.9).
и искомого решения во внутреннем узле. Поясним ситуацию на примере (рис.9).
Представим 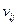 как линейную интерполяцию значений
как линейную интерполяцию значений 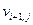 и
и 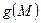 :
:
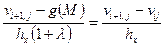 .
.
Отсюда
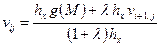 ,
, 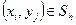 . (2.12')
. (2.12')
Это соотношение можно рассматривать как граничное условие в узлах сетки из 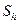 .
.
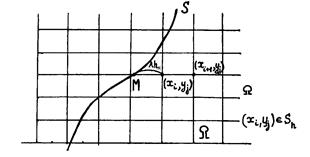
Рис.9. Аппроксимация граничного условия
Полученная в итоге система (2.11), (2.12') также аппроксимирует задачу (2.9), (2.10). Будем считать далее сетку просто квадратной.
