III. Порядок выполнения работы. 1. Установку после проверки работы схемы преподаватель или лаборант включает в сеть
1. Установку после проверки работы схемы преподаватель или лаборант включает в сеть.
2. Подвижный контакт (ползунок) установить посередине реохорда АС (х=0) и подобрать на магазине сопротивление так, чтобы ток в микроамперметре исчез. Проверка наличия тока осуществляется кратким нажатием красной кнопки на лицевой панели установки. При 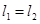 , как следует из (7.7)
, как следует из (7.7) 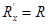 ; занести это значение Ri в таблицу. (Это опыт 1 из первой серии
; занести это значение Ri в таблицу. (Это опыт 1 из первой серии 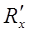 ).
).
3. Установить на магазине сопротивление меньше предыдущего на 10÷15% и перемещением ползунка Д по реохорду, вновь добиться исчезновения тока в микроамперметре. Измерить плечи моста 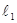 и
и 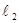 с учетом (7.9), данные занести в таблицу. (Это опыт 2 из первой серии).
с учетом (7.9), данные занести в таблицу. (Это опыт 2 из первой серии).
4. Теперь установить на магазине сопротивление больше измеренного в п.2 на 10÷15% , вновь перемещая движок реостата Д, добиться исчезновения тока в цепи. Записать показания l1 и l2 в таблицу. (Это опыт 3 из первой серии).
5. Включить в цепи второе неизвестное сопротивление 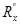 (см. на установке переключатель сопротивлений). Это вторая серия опытов. Проделать операции, аналогично пп. 2÷4.
(см. на установке переключатель сопротивлений). Это вторая серия опытов. Проделать операции, аналогично пп. 2÷4.
6. Установить переключатель установки в положение: «последовательное соединение» (это третья серия опытов); при этом сопротивления 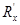 и
и 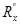 включены последовательно в цепь моста. Выполнить замеры по пп. 2÷4.
включены последовательно в цепь моста. Выполнить замеры по пп. 2÷4.
7. Переключатель установить в положение «параллельное соединение» (четвертая серия), выполнить вновь замеры по пп. 2÷4.
Таблица
| Опыты | R, Ом | 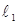 мм мм | 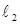 мм мм | 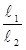 | 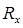 i Ом i Ом | 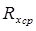 Ом Ом | 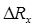 Ом Ом | 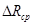 Ом Ом | ||
| Серия | №№ | |||||||||
I. 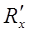 | ||||||||||
II. 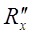 | ||||||||||
III 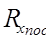 | ||||||||||
IV 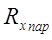 | ||||||||||
IV. Обработка результатов
1. Рассчитать Ri по формуле (7.7) для всех серий опытов.
2. По трем найденным значениям в каждой серии рассчитать среднее значение 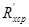 .
.
3. Найти абсолютные погрешности измерения сопротивлений как среднее значение модулей разностей между каждым сопротивлением в серии и их средним значением (см. введение (В.3) и (В.4)). Занести для каждой серии Δ Ri и Δ Rср в таблицу.
4. Для сравнения с опытными данными рассчитать эквивалентное (общее) сопротивление последовательно соединенных сопротивлений 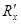 и
и 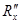 по формуле:
по формуле:
5. 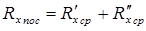 (7.10)
(7.10)
6. Рассчитать эквивалентное сопротивление при параллельном соединении:
7. 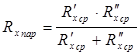 (7.11)
(7.11)
V. Выводы:
1) Измеренные сопротивления: Rх1 = … ± … Ом;
Rх2 = … ± … Ом;
Rпар = … ± … Ом;
Rпосл = … ± … Ом;
2) Измеренные и вычисленные эквивалентные (общие) сопротивления при последовательном и параллельном соединении сопротивлений R1 и R2 совпадают в пределах погрешности измерений.
Контрольные вопросы
1. Что называется "силой тока", "плотностью тока"? Каковы единицы их измерения в системе СИ?
2. Как связано электрическое сопротивление проводника с его длиной и поперечным сечением?
3. Напишите законы Ома в интегральной и дифференциальной формах.
4. Закон Джоуля-Ленца в интегральной и дифференциальой формах.
5. Что представляет собой мостовая схема постоянного тока?
6. Сформулируйте правила Кирхгофа.
7. Каковы особенности моста Уитстона? Почему для изготовления реохорда берут однородную калиброванную проволоку?
8. Напишите формулы для расчета эквивалентного сопротивления при последовательном соединения сопротивлений 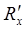 и
и 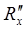 и при их параллельном соединении.
и при их параллельном соединении.
Литература
1. Белановский А.С. Основы биофизики в ветеринарии/ М.: Агропромиздат, 1989. – 272 с.
2. Ремизов А.Н. Медицинская и биологическая физика/ М.:Высшая школа, 1987. – 638 с.
3. Трофимова Т.И. Курс физики: Учеб. пособие. М: Высшая школа, 1985. 432 с.
Вопросы для защиты в форме круглого стола
По III разделу
«Электростатика. Постоянный ток»
| № Пп | Вопросы | Рекомендов. Литература | |
| № | Стр. | ||
| Электрический заряд. Закон сохранения заряда. Закон Кулона для взаимодействия точечных зарядов. | 128-129 | ||
| Напряженность и потенциал электрического поля. | 265-267 | ||
| Принцип суперпозиции для электрического поля. Диполь. | 132-133 270-271 | ||
| Клеточная мембрана. Калий – натриевый насос. | 132-137 | ||
| Биопотенциалы покоя и действия. Примеры мембранного потенциала для различных клеток. | 138-143 | ||
| Механизм передачи нервного импульса. | 141-144 | ||
| Методы измерения биопотенциалов. | 144-148 | ||
| Поляризация диэлектриков в электрическом поле. | 178-281 148-151 | ||
| Диэлектрическая проницаемость диэлектриков. Пьезоэлектрический эффект. | 141-143 282-284 | ||
| Конденсаторы. Электроемкость конденсаторов. | 149-151 | ||
| Энергия электрического поля. | 284-285 15-152 | ||
| Электрические свойства тканей организма. | 160-162 | ||
| Электрический ток, плотность тока. | 155-156 | ||
| Электросопротивление, электропроводность, удельное сопротивление, правила нахождения эквивалентного сопротивления при соединении проводников. | 156-157 | ||
| Закон Ома для тока I и плотности тока j. | |||
| Тепловое действие электрического тока, закон Джоуля-Ленца. | 158-159 | ||
| Действие постоянного электрического тока на живой организм. Электрофорез. | 162-164 | ||
| Методы электровоздействия в ветеринарии и животноводстве. | 169-172 |
Рекомендуемая таблица вариантов вопросов для проведения круглого стола
| В1 | В2 | В3 | В4 | В5 | В6 | В7 | В8 | В9 | В10 | |
РАЗДЕЛ IV. ЭЛЕКТРОМАГНЕТИЗМ
ВВЕДЕНИЕ
Общие положения
Подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи (движущиеся заряды) и постоянные магниты, возникает силовое поле, называемое магнитным. Однако, в отличие от электростатического поля, магнитное поле не является потенциальным, его работа на замкнутой траектории не равна нулю, магнитное поле имеет вихревой характер. Если индикатором наличия электрического поля является точечный положительный заряд, то индикатором магнитного поля является элементарный магнитный момент 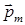 , которым обладает миниатюрный замкнутый плоский контур (рамка) площадью S с током I:
, которым обладает миниатюрный замкнутый плоский контур (рамка) площадью S с током I:
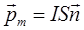 , (IV.1)
, (IV.1)
где 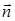 - единичный вектор нормали к плоскости рамки. (В постоянных магнитах суммарный магнитный момент атомов отличен от нуля и в отсутствии внешнего магнитного поля.)
- единичный вектор нормали к плоскости рамки. (В постоянных магнитах суммарный магнитный момент атомов отличен от нуля и в отсутствии внешнего магнитного поля.)
В магнитном поле рамка с током поворачивается, пока вектор 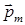 не установится вдоль силовых линий магнитно поля, при этом механический вращающий момент
не установится вдоль силовых линий магнитно поля, при этом механический вращающий момент 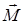 пропорционален как силе поля, характеризуемой вектором индукции
пропорционален как силе поля, характеризуемой вектором индукции 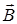 , так и величине магнитного момента
, так и величине магнитного момента 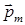 и равен их векторному произведению:
и равен их векторному произведению:
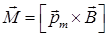 . (IV.2)
. (IV.2)
Это соотношение может служить для определения величины вектора индукции магнитного поля:
В=Ммакс/рm. (IV.3)
Единицей измерения индукции магнитного поля в системе СИ является Тесла: [B] = 1 Тл. Для магнитного поля, как и для электрического справедлив принцип суперпозиции:
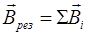 . (IV.4)
. (IV.4)
Как установил Ампер, на элемент проводника длиной dl с током I в магнитном поле с индукцией 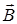 действует сила, равная векторному произведению:
действует сила, равная векторному произведению:
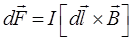 . (IV.5)
. (IV.5)
Частным случаем этой силы является сила Лоренца, действующая на движущийся со скоростью 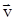 в магнитном поле c индукцией
в магнитном поле c индукцией 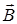 заряд q:
заряд q:
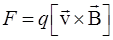 . (IV.6)
. (IV.6)
Но не только внешнее магнитное поле действует на движущиеся заряды и токи, но сами токи и движущиеся заряды создают вокруг себя магнитное поле. Согласно закону Био-Савара-Лапласа элемент проводника с током 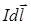 создает в точке наблюдения магнитное поле c индукцией
создает в точке наблюдения магнитное поле c индукцией 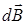 , определяемой векторным произведением:
, определяемой векторным произведением:
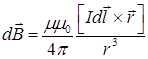 , (IV.7)
, (IV.7)
где 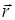 – радиус вектор, проведенный от элемента тока в точку наблюдения. Свободно движущийся со скоростью
– радиус вектор, проведенный от элемента тока в точку наблюдения. Свободно движущийся со скоростью 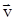 заряд q создает магнитное поле с индукцией:
заряд q создает магнитное поле с индукцией:
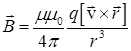 . (IV.8)
. (IV.8)
Здесь μ0 = 4π·10-7 Гн/м – магнитная постоянная; μ – относительная магнитная проницаемость среды. Для вакуума и воздуха μ = 1.
Однако, для характеристики магнитного поля, создаваемого токами, удобнее пользоваться понятием вектора напряженности 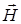 , который связан с вектором
, который связан с вектором 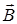 соотношением:
соотношением:
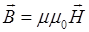 . (IV.9)
. (IV.9)
Единицей измерения напряженности магнитного поля 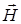 в системе СИ является 1 А/м.
в системе СИ является 1 А/м.
Индукция и напряженность магнитного поля в центре кругового витка радиуса R с током I равны соответственно :
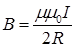 ,
, 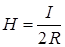 . (IV.10)
. (IV.10)
Величина вектора индукции и вектора напряженности магнитного поля, создаваемого длинным прямым проводом с током I на расстоянии r от него:
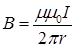 ,
, 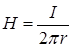 . (IV.11)
. (IV.11)
Величина напряженности магнитного поля в середине соленоида (узкая длинная катушка) или тороида (катушка, намотанная на тор) равна:
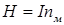 , (IV.12)
, (IV.12)
где nм – плотность намотки (количество витков на 1 м длины катушки).
Атомы всех веществ обладают собственными магнитными моментами 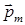 , которые во внешнем магнитном поле упорядочиваются. Возникающий при этом результирующий магнитный момент (называемый для единицы объема намагниченностью вещества) может быть направлен как навстречу внешнему полю (в диамагнетиках, μ<1), так и по направлению внешнего поля (в парамагнетиках, μ>1, и в ферромагнетиках, μ>>1). В случае ферромагнетика индукция внутри него намного больше, чем индукция, созданного теми же внешними токами магнитного поля в вакууме, что используется при изготовлении электромагнитов и трансформаторов.
, которые во внешнем магнитном поле упорядочиваются. Возникающий при этом результирующий магнитный момент (называемый для единицы объема намагниченностью вещества) может быть направлен как навстречу внешнему полю (в диамагнетиках, μ<1), так и по направлению внешнего поля (в парамагнетиках, μ>1, и в ферромагнетиках, μ>>1). В случае ферромагнетика индукция внутри него намного больше, чем индукция, созданного теми же внешними токами магнитного поля в вакууме, что используется при изготовлении электромагнитов и трансформаторов.
Принципом работы трансформатора служит явление электромагнитной индукции, которое заключается в возникновении в магнитном контуре э.д.с. индукции при изменении во времени величины магнитного потока Фм. Это явление описывается законом Фарадея:
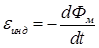 , (IV.13)
, (IV.13)
где 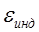 – электродвижущая сила, возникающая в контуре при изменении в нем магнитного потока, которым называют скалярное произведение:
– электродвижущая сила, возникающая в контуре при изменении в нем магнитного потока, которым называют скалярное произведение:
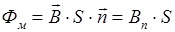 , (IV.14)
, (IV.14)
где 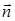 – единичный вектор нормали к поверхности S, Bn – нормальная к поверхности составляющая вектора индукции магнитного поля. Единицей измерения магнитного потока в СИ является Вебер: [Ф]=1 Вб
– единичный вектор нормали к поверхности S, Bn – нормальная к поверхности составляющая вектора индукции магнитного поля. Единицей измерения магнитного потока в СИ является Вебер: [Ф]=1 Вб
Знак «минус» в (IV.13) означает, что возникающий в замкнутом контуре индукционный ток стремится скомпенсировать или уменьшить изменение магнитного потока в соответствии с принципом Ле Шателье-Брауна.
При прохождении тока в контуре в нем создается магнитное поле, которое пересекает плоскость самого контура, и так возникает магнитный поток через этот контур (явление самоиндукции):
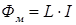 , (IV.15)
, (IV.15)
где L – индуктивность контура, которая в системе СИ измеряется в Генри:
[L] = 1 Гн. Тогда (IV.13) можно переписать:
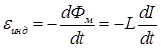 . (IV.13а)
. (IV.13а)
Энергия магнитного контура:
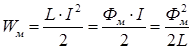 , (IV.16)
, (IV.16)
а энергия магнитного поля:
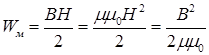 . (IV.17)
. (IV.17)
Дж. Максвелл создал единую теорию электромагнитного поля, сконцентрированную в системе уравнений, которые показывают, как изменяющееся магнитное поле создает электрическое поле, а движущиеся электрические заряды (т.е. изменение электрического поля) создают магнитное поле. Таким образом, в природе существует единое электромагнитное поле, которое распространяется в виде электромагнитных волн.
В живом организме циркулируют жидкости, которые являются электролитами, т.е. происходит направленное движение зарядов. Так что, с одной стороны, организм создает вокруг себя магнитное поле малой напряженности, которое может служить характеристикой его состояния, а с другой стороны – биотоки организма реагируют на внешнее магнитное поле. Последнее обстоятельство нашло широкое применение в физиотерапии. Однако, механизмы воздействия магнитного поля на работу тех или иных органов еще недостаточно изучены. Рассматриваются разные подходы: как через воздействие структурированной в магнитном поле воды, так и через воздействие силы Ампера на биотоки.
 |
ЛАБОРАТОРНАЯ РАБОТА № 8 (2-12)
