Линейные дифференциальные уравнения

Линейным дифференциальным уравнением первого порядканазывается уравнение

a₀(x)y¢ + a₁(x)y = B(x). (5.1.4)

При a₀ ¹ 0 его можно представить в виде:

y¢ + a(x)y = b(x), (5.1.5)

где a(x) = a₁(x)/a₀(x) и b(x) = B(x)/a₀(x).

Если правые части (5.1.4) и (5.1.5) равны нулю, то эти уравнения называются однородными, в противном случае – неоднородными.

Если в уравнении (5.1.4) a₀(x) = a₀ и a₁(x) = a₁, то есть эти функции являются константами, то уравнение (5.1.4) называется линейным дифференциальным уравнением первого порядка с постоянными коэффициентами.

Рассмотрим однородное уравнение

y¢ + ay = 0. (5.1.6)

Перепишем его в виде: 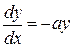или 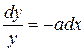. Последнюю формулу можно рассматривать как равенство дифференциалов функций одного и того же аргумента x. Интегрируя это равенство, получаем lny = –ax + C, или y = e^{–ax + C}, где C ‑ произвольная константа. Если теперь ввести обозначение e^C = A, то можно представить так называемое общее решение уравнения (5.1.6) в виде:

y = Ae^–ax. (5.1.7)

Это решение зависит от неопределенной константы A, придавая которой различные значения, можно получить все множество интегральных кривых уравнения (5.1.6). Если мы хотим найти интегральную кривую, проходящую через точку (x₁, y₁), то нужно подставить координаты точки в формулу (5.1.7) и определить значение константы A. С этим значением константы A формула (5.1.7) будет определять лишь одну интегральную кривую или так называемое частное решение уравнения (5.1.6).

Как правило, задача ставится так: найти решение уравнения (5.1.6) при условии

y(0) = y₀. (5.1.8)

Последняя формула называется начальным условием для уравнения (5.1.6).

Дифференциальное уравнение (5.1.6) при начальном условии (5.1.8) имеет единственное решение, которое определяется формулой

y(x) = y₀e^–ax. (5.1.9)

Заметим, что для задания начального условия, вообще говоря, не обязательно выбирать значение аргумента x, равное нулю. Как сказано выше, выделить единственное решение из множества, задаваемого формулой (5.1.7) (то есть определить константу А), можно с помощью любого соотношения y(x₁) = y₁, считая его начальным условием.

Если в уравнении (5.1.6) a = 0, то интегрирование приводит к решению y(x) = C, то есть к константе, которая при начальном условии (5.1.8) равна y₀. Таким образом решение y(x) сохраняет начальное значение y₀ при изменении x.

Рассмотрим теперь случай неоднородного дифференциального уравнения первого порядка. Пусть дано уравнение

y¢ + ay = b, ( b = cost ) (5.1.10)

с начальным условием y(0) = y₀.

Введем новую неизвестную 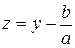(считаем, что a ¹ 0). Теперь уравнение (5.1.10) примет вид 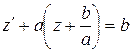или z¢ + az = 0. Как было показано выше, решением последнего уравнения является функция z = z₀e^–ax, где 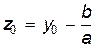. Возвращаясь к изначальной неизвестной, получаем решение уравнения (5.1.10) при заданном начальном условии:

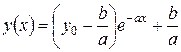
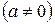. (5.1.11)

Если в уравнении (5.1.10) a = 0, то его решением при заданном начальном условии будет функция y(x) = bx + y₀.

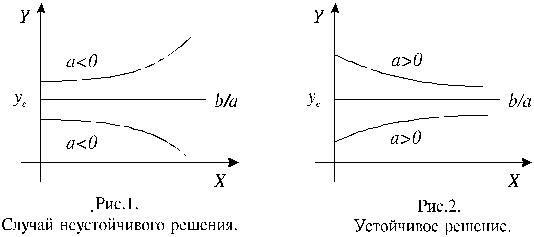
Заметим, что решение (5.1.11) состоит из двух частей: y_h = Ae^–ax ‑ решения однородного уравнения y¢ + ay = 0 и y₀(x) = b / a ‑ решения, которое назовем равновесным и которое получается, если в уравнении (5.1.10) положить y¢ = 0. Такое представление позволяет рассматривать решение (5.1.11) уравнения (5.1.10) как сумму равновесного или фиксированного значения y_e и отклонения или девиации y_h тра­ектории y(x) от равновесного значения. Это отклонение возрастает экспоненциально с ростом x при a < 0 и стремится к нулю при a > 0. В первом случае (a < 0) решение называется неустойчивым, а во втором – устойчивым (асимптотически устойчивым).