Непрерывность функции

Основные определения.

Пусть функция непрерывна в некоторой окрестности точки .

О п р е д е л е н и е 1. Функция называется непрерыв -ной в точке , если предел функции и её значение в этой точке совпадают, т .е. 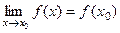. (1)

Так как 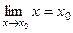, то соотношение (1) можно записать в виде 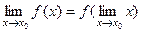, т.е. для непрерывной функции можно переставлять знак функции и знак предела.

О п р е д е л е н и е 2. Функция называется непрерыв- ной в точке , если для любой последовательности значе -ний аргумента , сходящейся к точке , соответствующая последовательность значений функции в этих точках 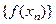сходится к .

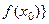О п р е д е л е н и е 3. Функция называется непрерыв- ной в точке , если для любого 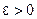существует 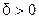, такое что для всех 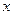, удовлетворяющих неравенству 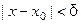, выполняется неравенство .

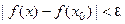ЗАМЕЧАНИЕ. Если

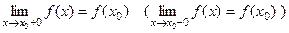, то функцию называют непрерывной в точке справа ( слева) Если функция непрерывна в точке справа и слева, то она непрерывна в этой точке.

Так как условия 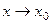и 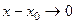равносильны, то неравенство (1) можем переписать в виде

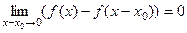. (2)

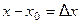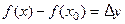Разность называется приращением аргумента в точке , а разность называется приращением функции в точке . Тогда равенство (2) в новых обозначениях принимает вид

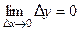, (3)

Соотношение (3) является ещё одним определением непрерывности функции:

О п р е д е л е н и е 4. Функция называется непрерыв- ной в точке , если её приращение в этой точке является бесконечно малой функцией при 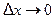, другими словами бесконечно малому приращению аргумента отвечает бесконечно малое приращение функции.

Арифметические действия с непрерывными функциями.

Если функции и 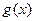непрерывны в точке , то функции 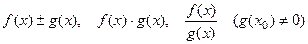также непрерывны в точке .

О п р е д е л е н и е 5. Функция непрерывна на отрезке 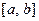, если она непрерывная в каждой точке этого отрезка.

ЗАМЕЧАНИЕ. Все элементарные функции непрерывны в своей области определения.

Классификация точек разрыва.

О п р е д е л е н и е 1. Точка называется точкой разрыва функции если в этой точке нарушается её непрерыв -ность.

В соответствии с определениями предыдущего пункта, функция будет непрерывной в точке если в этой точке выполняются все равенства

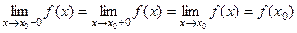(4)

В зависимости от того, какое из этих равенств не выпол -няется, получаем различные типы точек разрыва.

1. Устранимый разрыв.

Если 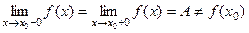. Этот разрыв можно устранить, доопределив функцию, положив 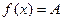. Например, 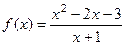имеет разрыв в точке 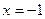, которая не входит в область определения. Но если преобра -зуем это выражение, то получим

,

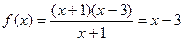т.е. график этой функции - это прямая; точке 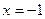отвечает выколотая точка на графике. Разрыв можно устранить, поло - жив .

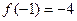2. Разрыв 1-го рода.

Если 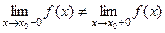, но оба эти предела конечны, то говорят, что в точке функция имеет разрыв

1-го рода (или «конечный скачок»). Рассмотрим на примерах:

1)

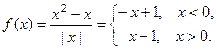
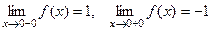. Они не совпадают, но оба конечны. Следовательно, в точке 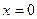функция имеет разрыв 1-го рода. На графике это выглядит таким образом:

y

х

-1

3. Разрыв 2-го рода.

Если хотя бы один из пределов 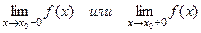равен бесконечности, то говорят, что в точке функция имеет разрыв 2-го рода. Например, 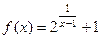. Точка 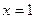не входит в область определения (точка возможного разрыва). Найдём в этой точке односторонние пределы:

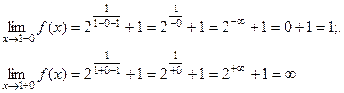
И ещё оценим поведение функции на бесконечности:

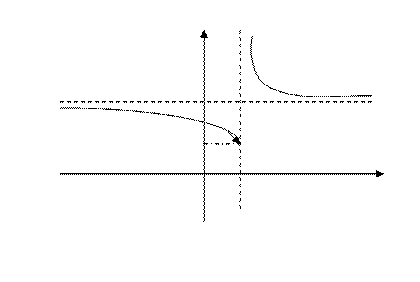
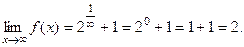
Построим схематический рисунок

У

0 х

О п р е д е л е н и е 2. Функция называется кусочно –непрерывной на отрезке 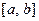, если она непрерывна во всех внутренних точках отрезка 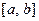, за исключением, может быть конечного числа точек разрыва 1-го рода и кроме того имеет односторонние пределы на концах отрезка. Функция называется кусочно-непрерывной на числовой прямой, если она кусочно непрерывна на любом отрезке.

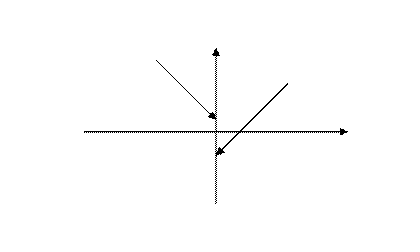
Например, рассмотрим функцию

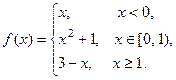
Она задана с помощью трёх функций, каждая из которых непрерывна на своём участке числовой прямой. Разрывы возможны только в точках, где функция меняет своё выражение, т.е. в точках и 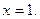Найдём односторонние пределы в этих точках

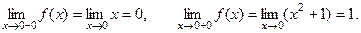
Пределы не совпадают, следовательно в точке 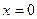функция имеет разрыв 1-го рода.

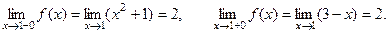
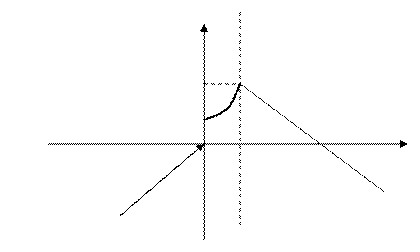Односторонние пределы совпадают. Это означает, что 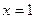- точка непрерывности функции. Согласно определению, эта функция кусочно-непрерывна на числовой прямой

У

0 1 3 х

Другим примером кусочно-непрерывной на всей числовой прямой функции может служить функция 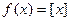(целая часть х), график которой приведён на рис. 4 из пункта 3.2.

Основные свойство непрерывных функций.

Сформулируем их в виде теорем, доказывать которые не будем.

1 ТЕОРЕМА 1 (об устойчивости знака непрерывной функции) Пусть функция непрерывна в точке , причём 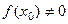. Тогда существует 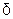- окрестность этой точки такая, что для всех 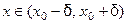функция имеет тот же знак, что и .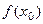

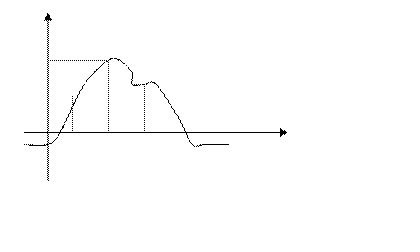Посмотрим, как это выглядит на рисунке

Y

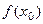
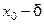
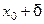x

2. Прохождение непрерывной функции через любое промежуточное значение.

ТЕОРЕМА 2 (1-я теорема Больцано – Коши). Пусть функция

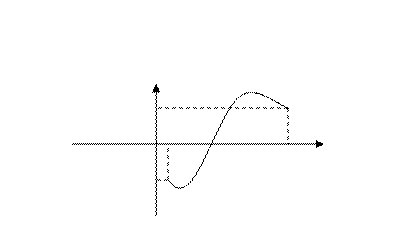
непрерывна на отрезке 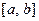и на концах

отрезка принимает значения разных знаков. Тогда

существует хотя бы одна точка 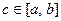, в которой

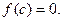
y

f(b)

a b x

f(a)

Теорема имеет простой геометрический смысл: непрерывная кривая при переходе из одной полуплоскости, границей кото- рой является ось 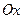, в другую пересекает эту ось.

ТЕОРЕМА 3 (2-я теорема Больцано – Коши) Пусть функция

непрерывна на отрезке 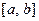, причём

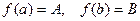. Пусть далее, 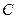- любое

число между 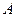и 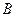. Тогда существует точ –

ка 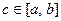, такая что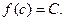

Другими словами, непрерывная функция при переходе от одного значения к другому принимает и все промежуточные значения.

СЛЕДСТВИЕ. Если функция определена на некотором промежутке 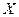, то множество её значений представляет аналогичный промежуток 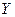(т.е. интервал переходит в интервал, отрезок в отрезок и т.п.)

3.. Ограниченность непрерывной функции на отрезке.

Напомним, что функция называется ограниченной на отрезке 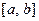, если существует число 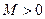такое, что для всех 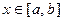выполняется неравенство 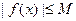или 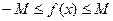, т.е. график функции не выходит из полосы, ограниченной прямыми 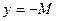и

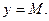
ТЕОРЕМА 4. (1-я теорема Вейерштрасса) Если функция

определена и непрерывна на отрезке

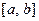, то она ограничена этом отрезке.

В §1 были введены понятия точной верхней грани 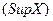и точной нижней грани ( 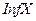) множества 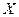. В соответствии с этим, точной верхней гранью функции называется точная верхняя грань множества её значений 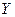и обознача -ется 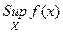. Аналогично определяется точная нижняя грань функции - 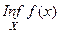. В том случае, если точные грани функции являются значениями функции, то говорят, что функция достигает своих точных граней.

ТЕОРЕМА 5 (2-я теорема Вейерштрасса). Если функция

непрерывна на отрезке 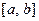, то она

достигает на этом отрезке своих точных

верхней и нижней граней, т. е. существуют

точки 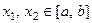, такие что

.

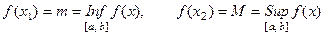Замечание 1 Так как непрерывная функция достигает на отрезке 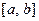своих точных верхней - 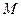и нижней -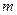

Граней, то можно назвать точную верхнюю грань - максималь- ным значением, а точную нижнюю грань - минимальным зна -чением функции . Поэтому теорему 5 можно перефор -мулировать следующим образом : непрерывная на отрезке функция имеет на этом отрезке максимальное и мини -мальное значение.

Разность между максимальным и минимальным значением непрерывной функции на отрезке 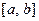называется колебанием непрерывной функции на этом отрезке и обозна –чается 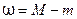, где .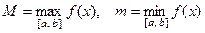

Понятие сложной функции.

О п р е д е л е н и е. Если на некотором промежутке 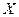определена функция 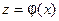с множеством значений 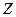, а на множестве 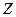определена функция 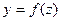, то функция 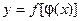называется сложной функцией от 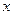, а пере -менная 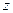- промежуточной переменной сложной функции.

Например, 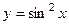- сложная функция : 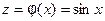, 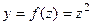; функция 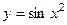- также сложная функция: .

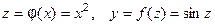ТЕОРЕМА. Пусть функция 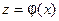непрерывна в точке , а функция 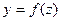непрерывна в точке 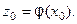Тогда сложная функция 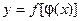непрерывна в точке

ФЕРЕНЦИРОВАНИЕ

5.1. Понятие производной.

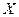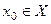Пусть на некотором промежутке определена функция . Возьмём любую точку и зададим аргументу 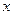в точке произвольное приращение 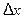такое, что точка 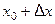также принадлежит 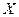. При этом функция получит приращение .

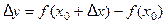О п р е е д е л е н и е. Производной функции в точке называется предел при 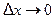отношения прира -щения функции в этой точке к приращению аргумента (при условии, что этот предел существует).

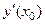Для обозначения производной функции в точке используют символы или .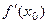

Итак, по определению

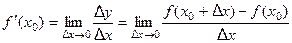
Если функция имеет конечную производную в каждой точке 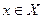, то производную 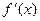можно рассмат -ривать как функцию от 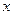, также определённую на .

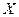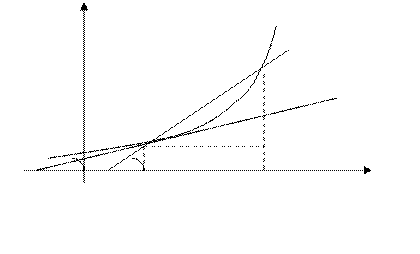
Геометрический смысл производной.

Пусть функция определена на интервале 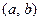и пусть точка 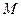на графике функции соответствует значению аргумента , а точка 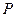- значению аргумента 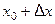. Проведём через точк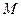и и 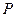прямую и назовём её секущей.. Обозначим через 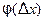угол между секущей и осью 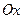. Очевидно, этот угол зависит от 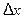(см. рис.) Если существует 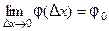то прямую с угловым коэффициентом 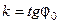, проходящую через точку

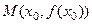, называют предельным положением секуще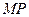й при .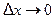

О п р е д е л е н и е . Касательной 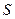к графику функции в точке 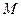называется предельное положение секуще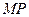й при ..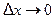

Таким образом, для существования касательной необходимо и достаточно существование предела .

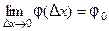Y

P

M

N

K L 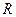x

O

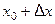
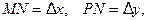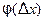Здесь, угол это угол 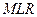, угол 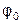- это угол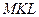

Докажем, что если функция имеет производную в точке , то существует касательная в точке 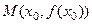, причём угловой коэффициент этой касательной (т.е. тангенс её наклона к оси 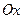) равен значению производной .

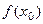Действительно, из треугольника 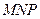получаем,

,

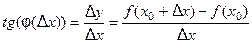Отсюда 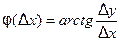. Перейдём в этом равенстве к пределу при 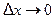. Так как существует производная

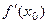, то существует и предел 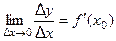. Тогда существует и предел

.

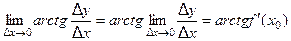Следовательно, существует и предел .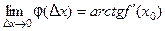

Но это и означает, что существует предельное положение секущей 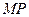, т.е. существование касательной. Уравнение касательной к графику функции в точке имеет вид .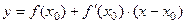

Понятие дифференцируемости функции.

О п р е д е л е н и е. Функция называется диффе- ренцируемой в точке , если её приращение 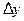в этой точке можно представить в виде:

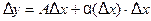, (1)

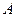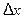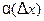где - некоторое число, не зависящее от , а - бесконечно малая функция при 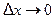, т.е.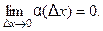

Для того, чтобы функция была дифференци -руема в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную. Поэтому для функции одной переменной дифференцируемость и существование производной - понятия равносильные. В формуле (1) .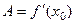

УТВЕРЖДЕНИЕ. Если функция дифференцируема в точке , то она непрерывна в этой точке.

В самом деле, если функция дифференцируема в точке , то 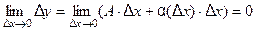, а это и означает непрерывность функции .

Обратное утверждение неверно, т.е. из непрерывности функции не следует её дифференцируемость. Примером непрерывной, но не дифференцируемой функции может служить функция .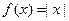

Понятие дифференциала.

Пусть функция дифференцируема в точке , т.е. её приращение в этой точке можно записать в виде:

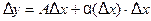
где 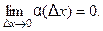Слагаемое 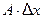- главная часть приращения функции.

О п р е д е л е н и е. Дифференциалом функции в точке называется главная, линейная относительно 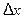часть приращения функции в этой точке, т.е. 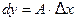(2)

Учитывая, что 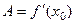, формулу (2) можем записать в виде 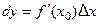. (3)

Если 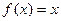, то по формуле (3), 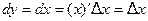, т.е. 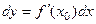. (4)

Геометрический смысл дифференциала. Дифференциал функции в точке равен приращению ординаты касательной в точке , в то время как 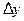- это приращения самой функции в точке и .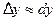

5.5 Правила дифференцирования.

Если функции 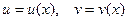дифференцируемы в точке 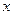, то сумма, разность, произведение и частное этих функций (при условии, что 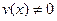) также дифференцируемы в этой точке и имеют место следующие формулы:

.

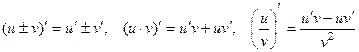Производная постоянной функции равна нулю ( .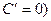

Правило дифференцирования сложной функции:

ТЕОРЕМА. Если функция 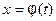имеет производную в

точке 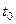, а функция имеет произ –

водную в соответствующей точке 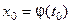, то

сложная функция 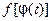также имеет произ-

водную в точке 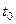и справедлива следующая

формула 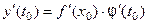. (1)

Доказательство. Так как функция дифференци -руема в точке , то приращение функции в этой точке может быть записано в виде

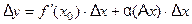, (2)

где 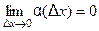. Поделив равенство (2) на 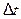, получим

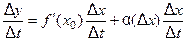. (3)

Равенство (3) справедливо при любых достаточно малых 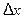. Возьмём 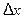равным приращению функции 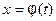, соот- ветствующему приращению 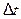аргумента 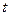в точке 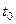, и устремим в этом равенстве 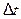к нулю. Так как, по условию, функция 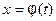имеет производную в точке 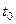, то она непрерывна в этой точке. Следовательно 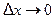при 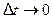. Но тогда и 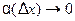, т.е. имеем 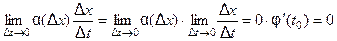(4)

Благодаря соотношению (4) существует предел правой части равенства (3) при 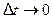, равный .

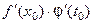Значит существует и предел при 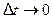левой части равен -ства (3), который, по определению производной, равен произ -водной сложной функции 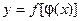в точке 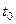и теорема доказана. Равенство (1) имеет место.

Например, вычислить производную 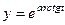, здесь

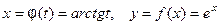, тогда по формуле (1), получим, .

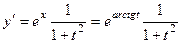5.6. Таблица производных сложных функций

Пусть 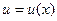, дифференцируемая функция. Тогда для производных сложных функций имеют место следующие формулы:

1. ;

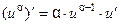2. ;

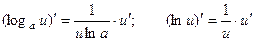3. $

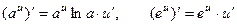4. ;

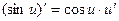5. ;

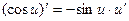6. ;

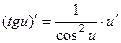7. ;

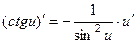8. :

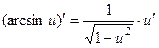9. ;

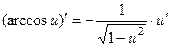10. ;

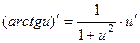11. .

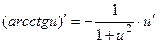В частности, если 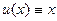, то 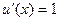, и получим обычную таблицу производных.

5.7 Производная неявно заданной функции.

Пусть зависимость между 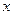и 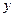задаётся неявно функцией 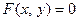, (1)

Причём, чаще всего, невозможно представление .

Тогда берут производную равенства (1), считая, что 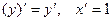. При этом, как правило, 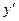зависит от 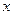и 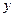Как выполняется дифференцирование в этом случае, лучше посмотреть на примерах.

1. Зависимость между 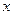и 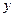задаётся формулой:

.

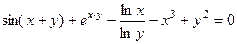Вычислим производную, учитывая формулу производной сложной функции и правила дифференцирования:

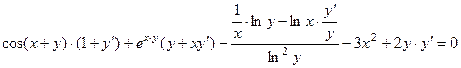
Преобразуем это выражение:

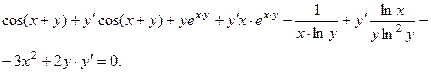
Перегруппируем это равенство, оставив слева слагаемые с 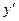, а все остальные слагаемые перенесём в правую часть

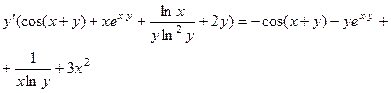
Отсюда получаем выражение для :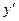

.

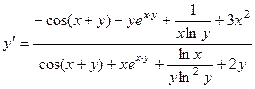2. Найт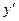и , или .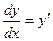

.

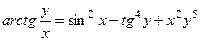Вычислим производную левой и правой части равенства:

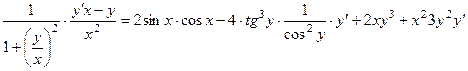
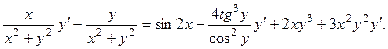
Тогда

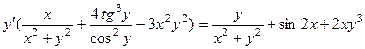
и окончательно,

.

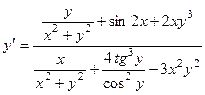5.8. Логарифмическое дифференцирование.

По правилу вычисления производной сложной функции, 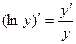. Эта формула позволяет вычислять производные довольно сложного вида. В первую очередь к ним относятся, так называемые показательно – степенные функции вида

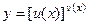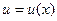, где и 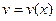- некоторые функции от 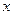( 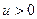), имеющие производные в точке .

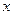Прологарифмируем эту функцию :

.

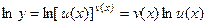Вычислим производную: .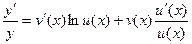
Отсюда, учитывая, что 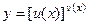, получим

.

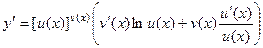ПРИМЕР. Вычислить производную функции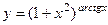

Прологарифмируем это выражение:

.

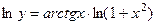Вычислим производную

,

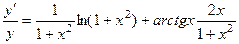тогда ,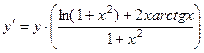

или .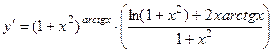

Учитывая свойства логарифмов (логарифм произведения равен сумме логарифмов, логарифм частного равен разности логарифмов, степень можно выносить за знак логарифма) этот же метод удобно использовать в случае, если функция задана только степенями, корнями, произведениями и дробями.

ПРИМЕР. Найти производную функции

.

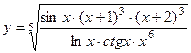Прологарифмируем эту функцию и используем свойства логарифма:

.

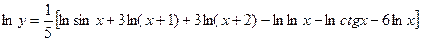Тогда

.

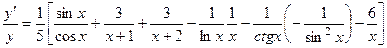
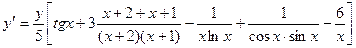Окончательно,

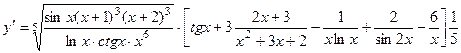Если бы мы попытались найти производную этой функции, непосредственно используя правила дифференцирования, получить результат было бы намного сложнее.

5.9. Производные высших порядков.

Как уже отмечалось, производная 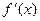функции сама является функцией от 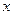. Следовательно, по отношению к ней, снова можно поставить вопрос о существовании произ –водной.