Определенный интеграл как функция верхнего предела. Формула Ньютона-Лейбница
Пусть функция f(t) определена и непрерывна на некотором промежутке, содержащем точку a. Тогда каждому числу x из этого промежутка можно поставить в соответствие число
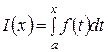 ,
,
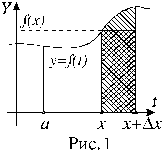 |
определив тем самым на промежутке функцию I(x), которая называется определенным интегралом с переменным верхним пределом. Отметим, что в точке x = a эта функция равна нулю. Вычислим производную этой функции в точке x. Для этого сначала рассмотрим приращение функции в точке x при приращении аргумента Dx:
DI(x) = I(x + Dx) – I(x) =
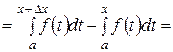
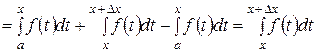 .
.
Как показано на рисунке 1, величина последнего интеграла в формуле для приращения DI(x) равна площади криволинейной трапеции, отмеченной штриховкой. При малых величинах Dx (здесь, так же как и везде в этом курсе, говоря о малых величинах приращений аргумента или функции, имеем в виду абсолютные величины приращений, так как сами приращения могут быть и положительными и отрицательными) эта площадь оказывается приблизительно равной площади прямоугольника, отмеченного на рисунке двойной штриховкой. Площадь прямоугольника определяется формулой f(x)Dx. Отсюда получаем соотношение
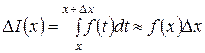 .
.
В последнем приближенном равенстве точность приближения тем выше, чем меньше величина Dx.
Из сказанного следует формула для производной функции I(x):
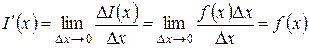 .
.
Производная определенного интеграла по верхнему пределу в точкеxравна значению подынтегральной функции в точкеx. Отсюда следует, что функция 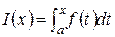 является первообразной для функции f(x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде
является первообразной для функции f(x), причем такой первообразной, которая принимает в точке x = a значение, равное нулю. Этот факт дает возможность представить определенный интеграл в виде
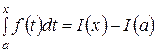 . (4.3.1)
. (4.3.1)
Пусть F(x) тоже является первообразной для функции f(x), тогда по теореме об общем виде всех первообразных функции I(x) = F(x) + C, где C — некоторое число. При этом правая часть формулы (1) принимает вид
I(x) – I(a) = F(x) + C – (F(a) +C) = F(x) – F(a). (4.3.2)
Из формул (1) и (2) после замены x на b следует формула для вычисления определенного интеграла от функции f(t) по промежутку [a;b]:
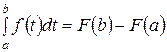 ,
,
которая называется формулойНьютона-Лейбница. Здесь F(x) — любая первообразная функции f(x).
Для того, чтобы вычислить определенный интеграл от функции f(x) по промежутку [a;b], нужно найти какую-либо первообразную F(x) функции f(x) и подсчитать разность значений первообразной в точках b и a. Разность этих значений первообразной принято обозначать символом 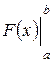 .
.
Приведем примеры вычисления определенных интегралов с помощью формулы Ньютона-Лейбница.
Примеры. 1. 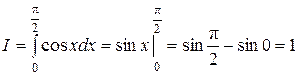 .
.
2. 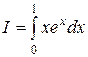 .
.
Сначала вычислим неопределенный интеграл от функции f(x) = xex. Используя метод интегрирования по частям, получаем: 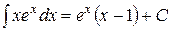 . В качестве первообразной функции f(x) выберем функцию ex(x – 1) и применим формулу Ньютона-Лейбница:
. В качестве первообразной функции f(x) выберем функцию ex(x – 1) и применим формулу Ньютона-Лейбница:
I = ex(x – 1) 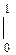 = 1.
= 1.
При вычислении определенных интегралов можно применять формулу замены переменной в определенном интеграле:
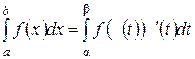 .
.
Здесь a и b определяются, соответственно, из уравнений j(a) = a; j(b) = b, а функции f, j, j¢ должны быть непрерывны на соответствующих промежутках.
Пример: 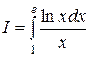 .
.
Сделаем замену: ln x = t или x = et, тогда если x = 1, то t = 0, а если x = e, то t = 1. В результате получим:
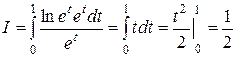 .
.
При замене переменной в определенном интеграле не нужно возвращаться к исходной переменной интегрирования.
