Нормальный закон распределения. Аналитическое и графическое представление. Использование для контроля технологического процесса

Нормальный закон распределения является наиболее распространенным на практике. Нормальным распределением (или законом Гаусса) называется распределение непрерывной случайной величины, плотность которой определяется по формуле

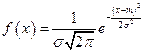, (1)

где m и 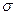– параметры распределения.

Функция нормального распределения имеет вид:

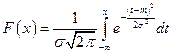. (2)

Для краткой записи нормального распределения с параметрами m и 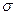используют обозначение 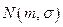. Параметр m равен математическому ожиданию, а параметр 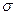– стандартному отклонению случайной величины X.

В частном случае параметры 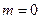, 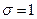. Нормальное распределение 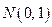называется стандартным нормальным распределением. В этом случае плотность распределения

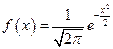. (3)

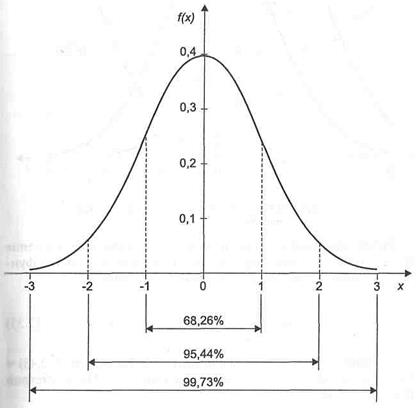
Кривая распределения, построенная по формуле (3), на рис.1 имеет колоколообразный вид, вертикальная ось является осюю симметрии, горизонтальная — асимптотой. Максимальное значение ординаты равно .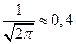

3 х

Рис. 1. Кривая стандартного нормального распределения

При значениях аргумента 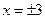значения функции близки к нулю: при общей площади под кривой распределения, равной единице, в этом диапазоне лежит 99,73%. Заметим, что в диапазоне 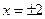лежит 95,44% площади под кривой распределения, а в диапазоне 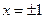– 68,26%.

При изменении параметра m график сдвигается вправо или влево так, что прямая 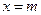– ось симметрии (рис. 2). При увеличении параметра 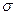(рис. 2) максимум кривой распределения снижается, при уменьшении 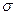кривая вытягивается вверх при этом по условию нормировки площадь под кривой распределения остается постоянной (и равной единице).

а =0,5

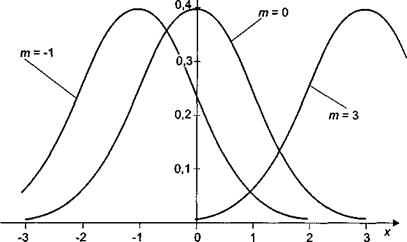
Рис. 2. Влияние параметра m на вид кривой нормального распределения

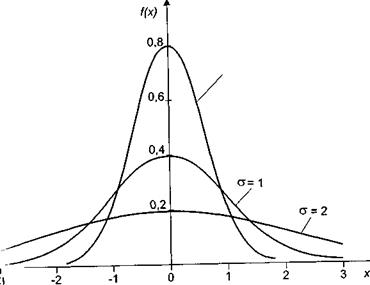
Рис. 3. Влияние параметра 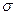на вид кривой нормального распределения

Вновь рассмотрим стандартное нормальное распределение 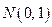. Функция такого распределения иногда называется функцией Лапласа, она имеет специальное обозначение

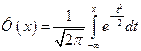. (4)

Эта функция табулирована (т.е. значения функции приводятся в специальных справочных таблицах). Например, 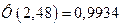. График функции показан на рис. 4. Из симметрии графика вытекает соотношение

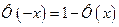. (5)

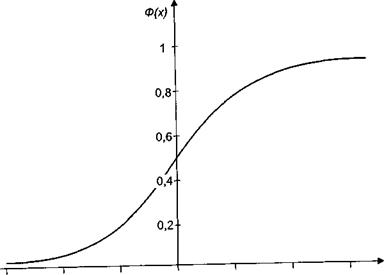
Рис. 4. График функции стандартного нормального распределения

Табулированы и квантили нормального распределения. Квантиль нормального распределения порядка р – это число 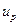для которого 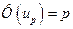. Например, 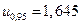. Из симметрии графика функции стандартного нормального распределения и формулы (5) вытекает полезное соотношение для квантилей:

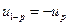. (6)

Можно установить связь между функцией распределения 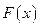для распределения 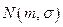и функцией стандартного нормального распределения:

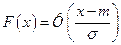. (7)

Вероятность попадания нормально распределенной случайной величины в интервал от 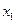до 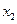определяется по формуле

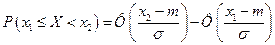. (8)

Часто в расчетах надо найти вероятность того, что случайная величина Х не слишком сильно отклонится от своего математического ожидания m:

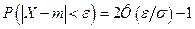. (9)

Пусть, например, 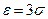. Используя таблицы функции стандартного нормального распределения, найдем:

,

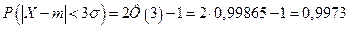поэтому вероятность того, что случайная величина отклонится от математического ожидания больше, чем на 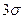, ничтожно мала: 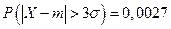. Такое событие практически невозможно. В связи с этим на практике часто используется так называемое правило «трех сигм»: отклонение нормально распределенной случайной величины от ее математического ожидания, как правило, не превышает утроенного стандартного отклонения. Данное правило широко используется для контроля технологического процесса при помощи контрольных карт. Более того, компанией Motorola разработана концепция «шести сигм», позволившая ей и другим компаниям сэкономить миллиарды долларов в результате резкого снижения уровня несоответствий, как в базовых процессах производства, так и в процессах обслуживания, управления финансами и людскими ресурсами. Согласно данной концепции предполагается возможность расширения допуска на контролируемый показатель качества до шести стандартных отклонений в каждую сторону от среднего значения, при этом уровень несоответствий составляет 2 на миллиард.

Широкое распространение нормального распределения обосновывается центральной предельной теоремой, которая устанавливает условия, в которых справедливо нормальное распределение.

Упрощенная формулировка теоремы такова. Пусть 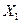, , 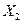…, 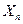– независимые одинаково распределенные случайные величины. Тогда при увеличении n закон распределения суммы этих величин неограниченно приближается к нормальному. Вопрос о том, при каких значениях n распределение можно приближении считать нормальным, зависит от точности расчетов.