Теплопроводность стенок при стационарном режиме

В технике часто возникают задачи определения температур­ного поля тела и установления законов передачи теплоты. В результате решения дифференциального уравнения тепло­проводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки. Следует отметить, что ана­литическое решение поставленной задачи возможно только для тел правильной геометрической формы и при достаточно прос­тых условиях однозначности. В остальных случаях эта задача решается численными или экспериментальными методами.

Рассмотрим несколько тел простой формы, таких как плоская стенка и полая труба, в случае стационарного распро­странения теплоты, для которых уравнение теплопроводности значительно упрощается.

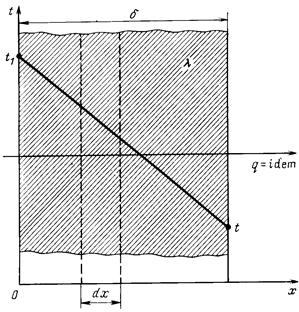
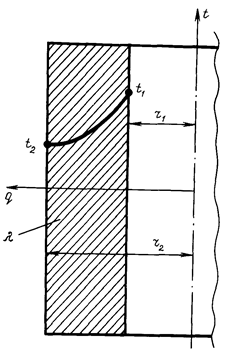
Теплопроводность через плоскую и цилиндрическую стен­ки. Рассмотрим однородную плоскую однослойную стенку тол­щиной 8 (рис. 2.4), имеющую неограниченную длину и ширину.

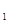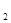На наружных поверхностях стенки поддерживаются постоянные температуры t и t . Коэффициент теплопровод­ности 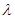стенки также постоянен. При стационарном режиме 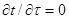и отсутствии внутренних источников теплоты 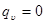, с учетом того, что в этом случае температура будет изменяться только в направлении оси ОХ, дифференциальное уравнение теплопроводности примет вид

Интегрируя уравнение (2.22), находим

После второго интегрирования получаем общий вид урав­нения распределения температур в плоских стенках:

Постоянные С 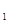и C 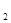в уравнении (2.24) определяются из граничных условий:

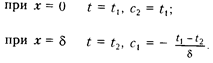
Подставляя значения постоянных С 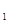и C 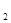в уравнение (2.24), получаем уравнение распределения температуры в рассматри­ваемой плоскости однослойной стенки

Уравнение (2.25) является уравнением прямой линии. Плотность теплового потока, проходящего через стенку в соответствии с законом Фурье, q = - 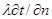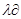. Учитывая, что

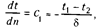
получим

Отношение 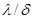((м² • К)/Вт) называется тепловой прово­димостью стенки, а обратная величина 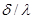((м² • К)/Вт)— тепловым или термическим сопротивлением стенки. Послед­нее представляет собой изменение температуры в стенке на единицу плотности теплового потока.

Тепловой поток, который передается через полную поверх­ность стенки,

Для многослойных стенок уравнение имеет вид

Величина 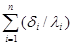называется полным термическим сопротивлением теплопроводности многослойной стенки.

При сравнении переноса теплоты через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности 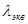многослойной стенки. Он равен коэффициенту тепло­проводности однородной стенки, толщина которой ∆ равна

толщине многослойной стенки 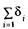, а термическое сопротивле­ние равно термическому сопротивлению рассматриваемой многослойной стенки:

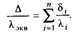
Отсюда

Из уравнения (2.29) следует, что эквивалентный коэффи­циент теплопроводности 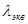зависит не только от теплофизических свойств слоев, но и от их толщины.

Графически распределение температур по сечению много­слойной стенки представляется ломаной линией. Температуру на границе соприкосновения слоев можно определить из уравнения

При исследовании стационарного процесса теплопроводно­сти в цилиндрической однослойной стенке (трубе) внутренним радиусом 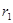, и наружным 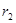(рис. 2.5) получаем уравнение распределения температуры

Уравнение (2.31) представляет собой уравнение логариф­мической кривой. То обстоятельство, что распределение темпе­ратуры в цилиндрической стенке является криволинейным, можно объяснить следующим. В случае плоской стенки плотность теплового потока остается одинаковой для всех изо­термических поверхностей и градиент температуры сохраняет для всех изотермических поверхностей постоянное значение. В случае цилиндрической стенки плотность теплового потока через любую изотермическую поверхность изменяется, так как величина поверхности зависит от радиуса (Н = 2 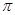rl), что приводит к изменению градиента температуры.

Для определения количества теплоты, проходящей через цилиндрическую поверхность Н в единицу времени, можно воспользоваться законом Фурье:

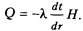
Подставляя значение градиента температуры и поверх­ности, получаем

Из уравнения (2.32) следует, что количество теплоты, проходящей через цилиндрическую стенку в единицу времени, полностью определяется заданными граничными условиями.

Тепловой поток (2.32) может быть отнесен либо к единице длины трубы, либо к единице внутренней или внешней поверхности.

Расчетная формула для плотности теплового потока, проходящего через единицу длины трубы, запишется как

Тепловой поток, отнесенный к единице длины трубы, изме­ряется в ваттах на метр (Вт/м) и называется линейной плот­ностью теплового потока. Как видно из уравнения (2.33), при неизменном отношении 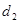/d линейная плотность теплового потока не зависит от поверхности цилиндрической стенки.

Тепловой поток через единицу внутренней поверхности можно рассчитать по формулам

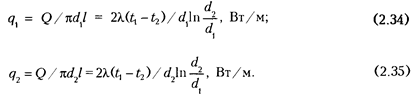
На основании полученного уравнения теплового потока на единицу длины трубы (2.33) можно получить уравнение теп­лового потока многослойной цилиндрической стенки. В этом случае необходимо выразить разности температур слоев из указанного уравнения, а затем сложить полученные резуль­таты. В результате получаем уравнение теплового потока многослойной цилиндрической стенки

Величина в знаменателе называется полным термическим сопротивлением многослойной цилиндрической стенки.

Уравнение (2.36) может быть использовано для определения темпе­ратур на границах любого слоя:

Таким образом, полученные уравнения температурного поля и теплового потока позволяют определить температуры в любой требуемой точке тела (пластины или цилиндра) и вычислить величину теплового потока.

Формула для расчета температурного поля шаровой стенки имеет вид

Тепловой поток определяют по уравнению

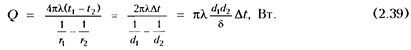
Указанные уравнения можно использовать для расчета тем­ператур в агрегатах и узлах автомобиля. Например, распре­деление температур по толщине двигателя или стенки кабины можно считать по уравнениям плоских стенок; карданных валов - по уравнениям цилиндрических стенок, заднего моста, главной передачи - по уравнениям шаровых стенок.