Свойства непрерывных функций. 1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций 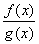 – есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Сложные функции
( Один из способов задания функции )
Пусть заданы две функции 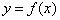 ,
, 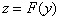 , причем область задания функции F содержит область значений функции
, причем область задания функции F содержит область значений функции 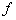 , тогда
, тогда 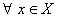 из этой области определения
из этой области определения 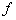 ставится в соответствие
ставится в соответствие 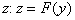 , где
, где 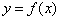 . Эта функция, определенная соответствием
. Эта функция, определенная соответствием 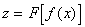 , называется сложной функцией, или суперпозицией функций
, называется сложной функцией, или суперпозицией функций 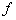 и F.
и F.
Примеры: 1. 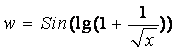 ; 2.
; 2. 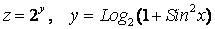 .
. 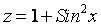 - явно задана.
- явно задана.
Классификация точек разрыва функции
Точка х0 называется точкой разрыва функции f(x), если f (x) в точке х0 не является непрерывной.
Это значит, что или не существует предела функции в данной точке, или этот предел не совпадает с тем значением, которое функция принимает в этой точке.
Точка х0 называется точкой разрыва первого рода функции f(x), если в этой точке функция f(x) имеет конечные, но не равные друг другу правый и левый пределы 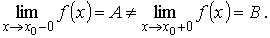 Точка х0 называется точкой разрыва второго рода функции f(x), если в этой точке функция f (x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Точка х0 называется точкой разрыва второго рода функции f(x), если в этой точке функция f (x) не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен.
Так для функции 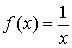 в точке х = 0 односторонние пределы равны
в точке х = 0 односторонние пределы равны 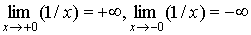 , то х = 0 является точкой разрыва второго рода
, то х = 0 является точкой разрыва второго рода
Основные правила нахождения пределов
Предел постоянной величины равен постоянной величине:
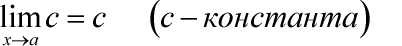
Предел суммы равен сумме пределов:
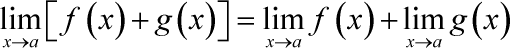
Предел разности равен разности пределов:
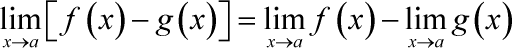
Предел произведения равен произведению пределов:
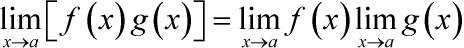
Предел отношения равен отношению пределов:
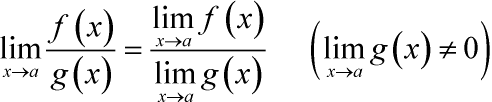
Предел функции в степени:
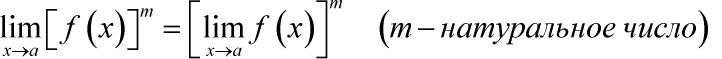
Предел корня из функции:
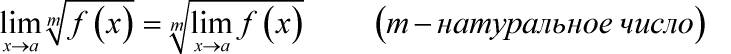
Свойства пределов функции
Пусть все функции, рассматриваемые ниже, определены на (а, в), кроме, быть может, фиксированной точки хо Î (а, в), тогда верны следующие свойства:
1. Если j ( х ) £ ¦ ( х) £ y ( х ) и
А =  =
= 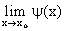 Þ
Þ  = A.
= A.
2. Если ¦(х) = С (сonst) Þ  ¦(x) = C .
¦(x) = C .
3. Если  cущ. Þ"с - const
cущ. Þ"с - const
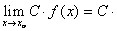

4. Если существуют конечные пределы  и
и 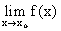 , тогда:
, тогда:
а) 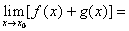
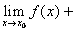
 ;
;
б) 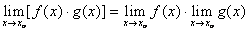 ;
;
в) 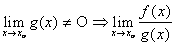 =
=  .
.
Все эти свойства доказываются одинаковым методом, основанным на соответствующих свойствах пределов последовательностей. Для доказательства этих свойств введем понятие бесконечно малых и бесконечно больших функций
18. Определение производной и дифференцируемости функции.
