Распределение непрерывных случайных величин по закону гаусса (нормальное распределение)

Непрерывная случайная величина Х имеет нормальное распределение (распределение по закону Гаусса), если ее плотность вероятности описывается функцией: 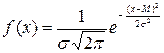, где М – математическое ожидание, 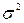- дисперсия, 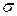-среднее квадратическое отклонение этой случайной величины.

Кривая распределения имеет симметричную относительно математического ожидания колоколообразную форму (рис. 5.). Положение и крутизна кривой нормального распределения зависит от ее параметров М и : , .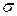

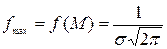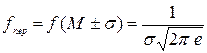Попадание случайной величины в любой интервал (a;b) определяется, как и для любой непрерывно распределенной величины по формуле: 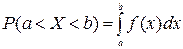, т.е. в нашем случае получается 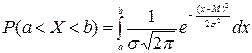, а это «неберущийся» интеграл Гаусса, значения которого можно вычислить по специальной таблице (табл.2.). Т.о., 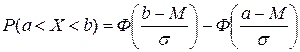, причем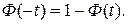

Пример 16.

Случайная величина Х имеет нормальное распределение с M=3 и σ=2. Найти вероятность того, что Х примет свои значения из интервала (2; 5).

Решение:

Используя формулу вероятности попадание случайной величины в любой интервал (a;b) и значения функции Гаусса из таблицы 2, имеем:

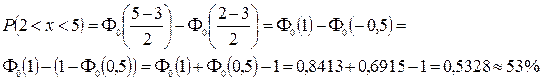
Среди множества значений, которые принимает нормально распределенная случайная величина Х, выделяют 3 стандартных интервала содержащих, соответственно, 68, 95 и 99% всех значений данной случайной величины. Размеры этих интервалов определяются для любой величины ее математическим ожиданием и средним квадратическим отклонением:

· 1-ый стандартный интервал 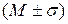, причем ;

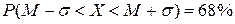· 2-ой стандартный интервал 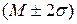, причем ;

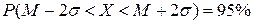· 3-ий стандартный интервал 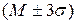, причем .

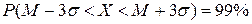Рис. 5. График кривой нормального распределения.

ТАБЛИЦЫ ДЛЯ РЕШЕННИЯ ЗАДАЧ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ

Таблица 1.

Значения функции Лапласа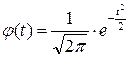

t
0,0	0,398942	0,398922	0,398862	0,398763	0,398623	0,398444	0,398225	0,397966	0,397668	0,397330
0,1	0,396953	0,396536	0,396080	0,395585	0,395052	0,394479	0,393868	0,393219	0,392531	0,391806
0,2	0,391043	0,390242	0,389404	0,388529	0,387617	0,386668	0,385683	0,384663	0,383606	0,382515
0,3	0,381388	0,380226	0,379031	0,377801	0,376537	0,375240	0,373911	0,372548	0,371154	0,369728
0,4	0,368270	0,366782	0,365263	0,363714	0,362135	0,360527	0,358890	0,357225	0,355533	0,353812
0,5	0,352065	0,350292	0,348493	0,346668	0,344818	0,342944	0,341046	0,339124	0,337180	0,335213
0,6	0,333225	0,331215	0,329184	0,327133	0,325062	0,322972	0,320864	0,318737	0,316593	0,314432
0,7	0,312254	0,310060	0,307851	0,305627	0,303389	0,301137	0,298872	0,296595	0,294305	0,292004
0,8	0,289692	0,287369	0,285036	0,282694	0,280344	0,277985	0,275618	0,273244	0,270864	0,268477
0,9	0,266085	0,263688	0,261286	0,258881	0,256471	0,254059	0,251644	0,249228	0,246809	0,244390
1,0	0,241971	0,239551	0,237132	0,234714	0,232297	0,229882	0,227470	0,225060	0,222653	0,220251
1,1	0,217852	0,215458	0,213069	0,210686	0,208308	0,205936	0,203571	0,201214	0,198863	0,196520
1,2	0,194186	0,191860	0,189543	0,187235	0,184937	0,182649	0,180371	0,178104	0,175847	0,173602
1,3	0,171369	0,169147	0,166937	0,164740	0,162555	0,160383	0,158225	0,156080	0,153948	0,151831
1,4	0,149727	0,147639	0,145564	0,143505	0,141460	0,139431	0,137417	0,135418	0,133435	0,131468
1,5	0,129518	0,127583	0,125665	0,123763	0,121878	0,120009	0,118157	0,116323	0,114505	0,112704
1,6	0,110921	0,109155	0,107406	0,105675	0,103961	0,102265	0,100586	0,098925	0,097282	0,095657
1,7	0,094049	0,092459	0,090887	0,089333	0,087796	0,086277	0,084776	0,083293	0,081828	0,080380
1,8	0,078950	0,077538	0,076143	0,074766	0,073407	0,072065	0,070740	0,069433	0,068144	0,066871
1,9	0,065616	0,064378	0,063157	0,061952	0,060765	0,059595	0,058441	0,057304	0,056183	0,055079
2,0	0,053991	0,052919	0,051864	0,050824	0,049800	0,048792	0,047800	0,046823	0,045861	0,044915
2,1	0,043984	0,043067	0,042166	0,041280	0,040408	0,039550	0,038707	0,037878	0,037063	0,036262
2,2	0,035475	0,034701	0,033941	0,033194	0,032460	0,031740	0,031032	0,030337	0,029655	0,028985
2,3	0,028327	0,027682	0,027048	0,026426	0,025817	0,025218	0,024631	0,024056	0,023491	0,022937
2,4	0,022395	0,021862	0,021341	0,020829	0,020328	0,019837	0,019356	0,018885	0,018423	0,017971
2,5	0,017528	0,017095	0,016670	0,016254	0,015848	0,015449	0,015060	0,014678	0,014305	0,013940
2,6	0,013583	0,013234	0,012892	0,012558	0,012232	0,011912	0,011600	0,011295	0,010997	0,010706
2,7	0,010421	0,010143	0,009871	0,009606	0,009347	0,009094	0,008846	0,008605	0,008370	0,008140
2,8	0,007915	0,007697	0,007483	0,007274	0,007071	0,006873	0,006679	0,006491	0,006307	0,006127
2,9	0,005953	0,005782	0,005616	0,005454	0,005296	0,005143	0,004993	0,004847	0,004705	0,004567
3,0	0,004432	0,004301	0,004173	0,004049	0,003928	0,003810	0,003695	0,003584	0,003475	0,003370
3,1	0,003267	0,003167	0,003070	0,002975	0,002884	0,002794	0,002707	0,002623	0,002541	0,002461
3,2	0,002384	0,002309	0,002236	0,002165	0,002096	0,002029	0,001964	0,001901	0,001840	0,001780
3,3	0,001723	0,001667	0,001612	0,001560	0,001508	0,001459	0,001411	0,001364	0,001319	0,001275
3,4	0,001232	0,001191	0,001151	0,001112	0,001075	0,001038	0,001003	0,000969	0,000936	0,000904
3,5	0,000873	0,000843	0,000814	0,000785	0,000758	0,000732	0,000706	0,000681	0,000657	0,000634
3,6	0,000612	0,000590	0,000569	0,000549	0,000529	0,000510	0,000492	0,000474	0,000457	0,000441
3,7	0,000425	0,000409	0,000394	0,000380	0,000366	0,000353	0,000340	0,000327	0,000315	0,000303
3,8	0,000292	0,000281	0,000271	0,000260	0,000251	0,000241	0,000232	0,000223	0,000215	0,000207
3,9	0,000199	0,000191	0,000184	0,000177	0,000170	0,000163	0,000157	0,000151	0,000145	0,000139

Для вычисления значения функции при отрицательных значениях аргумента используется соотношение .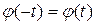

Таблица 2.

Значения функции 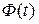для решения задач

На закон нормального распределения

T	Ф(t)	t	Ф(t)	t	Ф(t)	t	Ф(t)
	0,5		0,8413		0,9772		0,9986
0,1	0,5398	1,1	0,8643	2,1	0,9821	3,1	0,999
0,2	0,5793	1,2	0,884	2,2	0,9861	3,2	0,9993
0,3	0,6179	1,3	0,9032	2,3	0,9893	3,3	0,9995
0,4	0,6554	1,4	0,9192	2,4	0,9918	3,4	0,9997
0,5	0,6915	1,5	0,9332	2,5	0,9938	3,5	0,9998
0,6	0,7257	1,6	0,9452	2,6	0,9953	3,6	0,9998
0,7	0,758	1,7	0,9554	2,7	0,9965	3,7	0,9999
0,8	0,7881	1,8	0,9641	2,8	0,9974	3,8	0,9999
0,9	0,8159	1,9	0,9713	2,9	0,9981	3,9