Решение задания типа 61-70
Исследовать методами дифференциального исчисления функцию 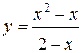 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
Решение. Исследование функций и построение их графиков проводится по следующей схеме:
1) найти область определения функции 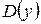 ; исследовать функцию на четность и нечетность;
; исследовать функцию на четность и нечетность;
2) исследовать функцию на непрерывность; найти точки разрыва (если они существуют) и установить характер разрыва;
3) найти асимптоты графика функции;
4) найти интервалы возрастания и убывания функции и ее экстремумы;
5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба;
6) найти точки пересечения графика функции с осями координат;
7) построить график функции.
1) Область определения функции: 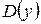 =
= 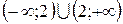 . Проверим функцию на четность, нечетность:
. Проверим функцию на четность, нечетность: 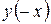 =
= 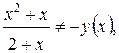
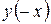
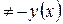 . Значит функция ни четная, ни нечетная.
. Значит функция ни четная, ни нечетная.
2) Точка разрыва х = 2, причем 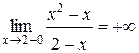 ,
, 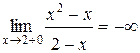 , следовательно, х = 2 является вертикальной асимптотой графика функции.
, следовательно, х = 2 является вертикальной асимптотой графика функции.
3) Найдем наклонные асимптоты 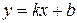 , для этого вычислим
, для этого вычислим 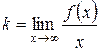 =
= 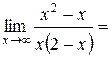
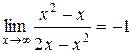 ;
;
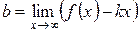 =
= 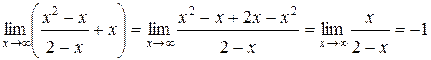 .
.
Таким образом, прямая 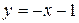 является наклонной асимптотой графика функции.
является наклонной асимптотой графика функции.
4) Интервалы возрастания, убывания и экстремумы определим по следующей схеме:
а) находим первую производную 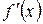 ;
;
б) находим критические точки, т.е. точки, в которых 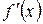 =0 или
=0 или 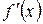 не существует;
не существует;
в) область определения разбиваем критическими точками на конечное число интервалов монотонности, в каждом из которых 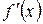 имеет строго определенный знак;
имеет строго определенный знак;
г) в соответствии с достаточными условиями определяем интервалы возрастания, убывания функции и ее экстремумы.
Итак,
а) 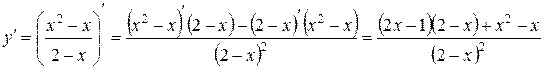 =
=
= 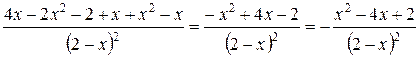 .
.
б) критические точки находим из уравнения 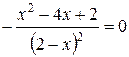 . Отсюда
. Отсюда 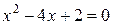 , следовательно,
, следовательно, 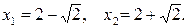
в) область определения разбиваем критическими точками на интервалы монотонности следующим образом:

г) вычисляем экстремумы функции:
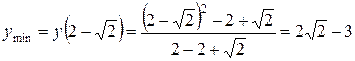 ;
;
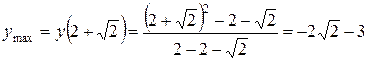 .
.
5) Найдем интервалы выпуклости, вогнутости кривой и ее точки перегиба. Вычислим 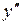 :
:
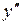 =
= 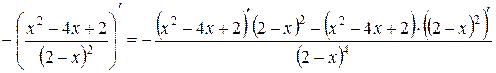 =
=
= 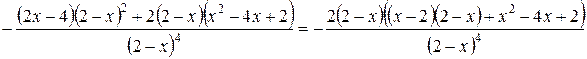 =
=
= 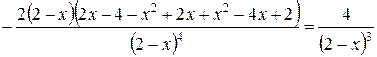 ;
;
Найдем точки, в которых 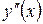 =0 или
=0 или 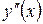 не существует:
не существует:
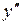 =
= 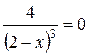 - нет решений,
- нет решений, 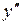 не существует, если
не существует, если 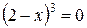 , откуда
, откуда 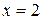 .
.
Находим интервалы знакопостоянства для 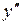 :
:

Так как 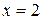 не входит в
не входит в 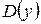 , то точек перегиба графика нет.
, то точек перегиба графика нет.
6) Найдем точки пересечения графика с осями координат: если 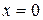 , то
, то 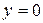 , если
, если 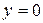 , то
, то 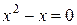 или
или 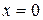 и
и  . Следовательно, график проходит через точки
. Следовательно, график проходит через точки 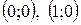 .
.
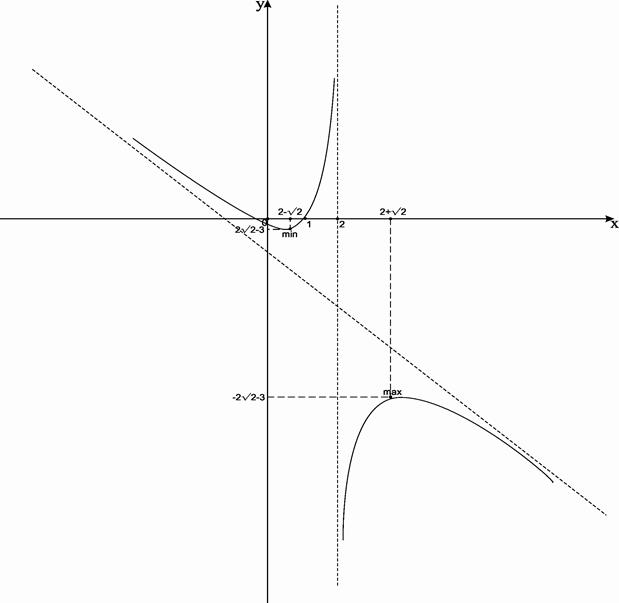
7) Используя полученные результаты исследования, строим график функции.
Методические указания для выполнения контрольной работы № 2.
Решение заданий типа 71-80.Даны функция трех переменных 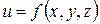 , точка
, точка 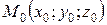 и вектор
и вектор 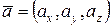 . Найти: 1) градиент функции
. Найти: 1) градиент функции 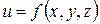 в точке
в точке 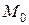 ; 2) производную функции
; 2) производную функции 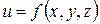 в точке
в точке 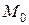 по направлению вектора
по направлению вектора 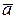 .
.
Например, 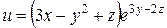 ,
, 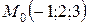 ,
, 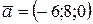 .
.
Решение. 1) Градиент функции 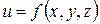 в точке
в точке 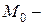 это вектор, равный:
это вектор, равный:
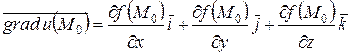 , где
, где 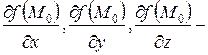 значения частных производных функции
значения частных производных функции 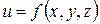 по переменным x,y,z, соответственно, в точке М0.
по переменным x,y,z, соответственно, в точке М0.
Найдем частные производные функции 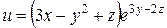 . Частная производная по переменной х является обыкновенной производной функции одной переменной х при фиксированном значении переменных у и z и обозначается
. Частная производная по переменной х является обыкновенной производной функции одной переменной х при фиксированном значении переменных у и z и обозначается 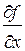 . Т.о.
. Т.о. 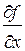 =
= 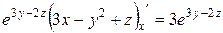 .
.
При вычислении 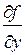 (частной производной по переменной у) переменные х и z считают постоянными. Тогда
(частной производной по переменной у) переменные х и z считают постоянными. Тогда
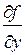 =
= 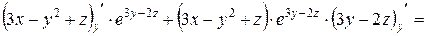 =
= 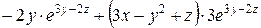 =
= 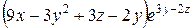 .
.
При вычислении 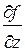 (частной производной по переменной z) переменные х и y считают постоянными. Тогда
(частной производной по переменной z) переменные х и y считают постоянными. Тогда
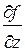 =
= 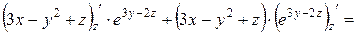
= 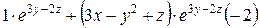 =
= 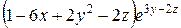 .
.
Вычислим значения частных производных в точке 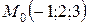 :
:
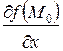 =
= 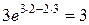 ;
; 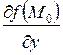 =
= 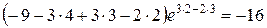 ;
; 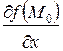 =
= 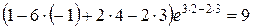 .
.
Тогда 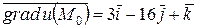 .
.
2) Производная функции 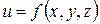 в точке
в точке 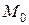 по направлению вектора
по направлению вектора 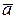 вычисляется по формуле
вычисляется по формуле
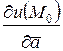 =
= 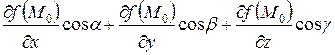 ,
,
где 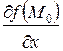 =3,
=3, 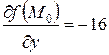 ,
, 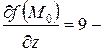 вычислены в предыдущем задании этой задачи, а
вычислены в предыдущем задании этой задачи, а 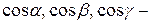 направляющие косинусы вектора
направляющие косинусы вектора 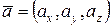 , которые вычисляются по формулам
, которые вычисляются по формулам 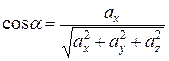 ,
, 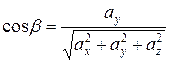 ,
, 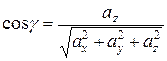 . Для вектора
. Для вектора 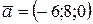 они равны
они равны 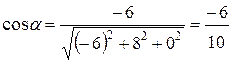 ;
; 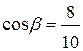 ;
; 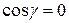 . Тогда производная функции по направлению вектора
. Тогда производная функции по направлению вектора 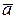 в точке
в точке 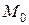 равна
равна
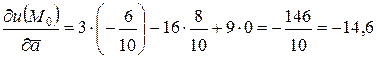 .
.
Решения заданий типа 81-90.Производятся два вида товаров, объемы производства которых х и у, цены на эти товары 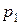 и
и 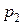 , соответственно, затраты на производство задаются функцией издержек
, соответственно, затраты на производство задаются функцией издержек 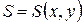 . Определить при каких объемах производства данных товаров прибыль будет максимальной; найти ее максимальное значение.
. Определить при каких объемах производства данных товаров прибыль будет максимальной; найти ее максимальное значение.
Например, 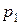 =8 (у.е.),
=8 (у.е.), 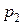 =10 (у.е.),
=10 (у.е.), 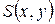 =
= 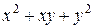 (у.е.).
(у.е.).
Решение. Так как товары производятся в объемах х и у, то функция прибыли 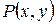 будет иметь вид
будет иметь вид 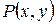 =
= 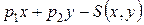 или
или 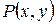 =
= 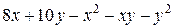 . Требуется найти значения переменных х и у, при которых эта функция примет максимальное значение, при условии, что
. Требуется найти значения переменных х и у, при которых эта функция примет максимальное значение, при условии, что 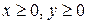 . Т.е. надо найти максимум функции двух переменных
. Т.е. надо найти максимум функции двух переменных 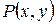 .
.
Для этого найдем точки возможного экстремума этой функции, т.е. точки в которых 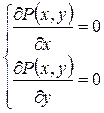 . В нашей задаче
. В нашей задаче 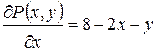 ;
; 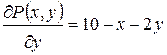 , поэтому система имеет вид:
, поэтому система имеет вид: 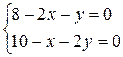 . Решая ее, находим
. Решая ее, находим 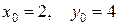 , т.е. точка
, т.е. точка 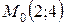 является точкой возможного экстремума. Если в точке
является точкой возможного экстремума. Если в точке 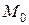 определитель
определитель 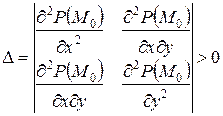 и
и 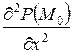 < 0, то точка
< 0, то точка 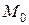 является точкой локального максимума функции
является точкой локального максимума функции 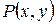 . Здесь
. Здесь 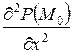 ,
, 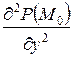 ,
, 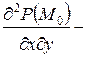 значения частных производных второго порядка функции
значения частных производных второго порядка функции 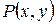 в точке
в точке 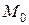 .
.
Вычислим эти частные производные: 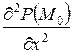 =
= 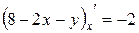 ;
; 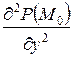 =
= 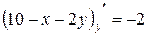 ;
; 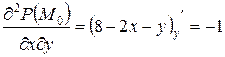 . Тогда
. Тогда 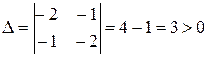 и
и 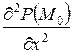 =
= 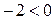 , значит точка
, значит точка 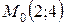 является точкой экстремума функции прибыли
является точкой экстремума функции прибыли 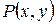 . Это означает, что, если объемы производства товаров первого и второго видов будут равны 2 и 4, соответственно, то прибыль будет максимальной и ее значение будет равно
. Это означает, что, если объемы производства товаров первого и второго видов будут равны 2 и 4, соответственно, то прибыль будет максимальной и ее значение будет равно 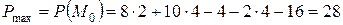 (у.е.).
(у.е.).
