Алгоритм симплексного метода
Для того чтобы решить задачу симплексным методом (методом последовательного улучшения плана), необходимо выполнить следующее:
1. Привести задачу линейного программирования к каноническому виду
2. найти начальное опорное решение с единичным базисом и коэффициенты разложения векторов условий по базису опорного решения.
Если опорное решение отсутствует, то задача не имеет решения в силу несовместности системы ограничений.
3.Вычислить оценки разложений векторов условий по базису опорного решения и заполнить симплексную таблицу.
4. Если выполняется признак единственности оптимального решения то решение задачи заканчивается.
5. Если выполняется условие существования множества оптимальных решений  (следствие 4 из теоремы 2.3.1.), то путем простого перебора находят все оптимальные решения.
(следствие 4 из теоремы 2.3.1.), то путем простого перебора находят все оптимальные решения.
6. Если выполняются условия следствия 5 теоремы об улучшении опорного решения, то задача не имеет решения ввиду неограниченности целевой функции.
7. Если пункты 4-6 алгоритма не выполняются, находят новое опорное решение с использованием условий следствия 1 и возвращаются к пункту 3.
Пример. Решить симплексным методом задачу:

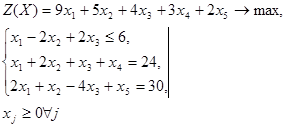
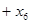
Р е ш е н и и е. Приводим задачу к каноническому виду. Для этого в левую часть первого ограничения-неравенства типа «≤» вводим дополнительную переменную 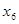 с коэффициентом +1. В целевую функцию переменная
с коэффициентом +1. В целевую функцию переменная 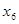 входит с коэффициентом 0 (т.е. не входит). Получаем:
входит с коэффициентом 0 (т.е. не входит). Получаем:
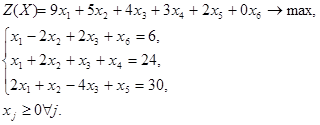
Находим начальное опорное решение. Для этого свободные (неразрешенные) переменные приравниваем к нулю 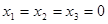 . Получаем опорное решение
. Получаем опорное решение 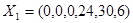 с единичным базисом
с единичным базисом 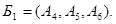
Вычисляем оценки разложений векторов условий по базису опорного решения, используя формулу (2.2.1).
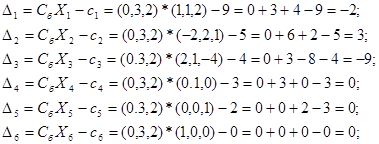
Оценки векторов, входящих в базис, всегда равны нулю. Обычно эти вычисления проводятся устно. Опорное решение, коэффициенты разложений и оценки разложений векторов условий по базису опорного решения записываются в симплексную таблицу (табл.2.4.1). Сверху над таблицей для удобства вычислений оценок записываются коэффициенты целевой функции. В первом столбце «Б» записываются векторы, входящие в базис опорного решения. Порядок записи этих векторов в симплексной таблице соответствует номерам разрешенных неизвестных в уравнениях-ограничениях. Во втором столбце таблицы « 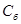 » записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце «
» записываются коэффициенты целевой функции при базисных переменных в том же порядке. При правильном расположении коэффициентов целевой функции в столбце « 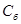 » оценки единичных векторов, входящих в базис, всегда равны нулю.
» оценки единичных векторов, входящих в базис, всегда равны нулю.
В последней строке таблицы с оценками 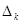 в столбце «
в столбце « 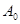 » записывается значение целевой функции на опорном решении
» записывается значение целевой функции на опорном решении 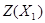
Таблица 2.4.1
9 5 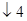 3 2 0
3 2 0
| Б | 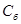 | 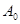 | 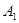 | 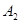 | 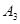 | 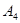 | 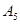 | 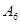 | 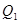 | 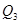 |
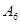 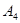 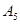 | -2 | -4 | - | |||||||
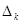 | -2 | -9 |
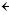
Начальное опорное решение не является оптимальным, так как оценки 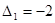 ,
, 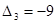 для векторов
для векторов 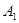 и
и 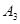 противоречат признаку оптимальности. Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов условий.
противоречат признаку оптимальности. Для оптимальности опорного решения в задаче на максимум требуется неотрицательность оценок для всех векторов условий.
По теореме об улучшении опорного решения (см. теорему 2.1.1), если в задаче на максимум хотя бы один вектор имеет отрицательную оценку, то можно найти новое опорное решение, на котором значение целевой функции будет больше.
Определим, введение какого из двух векторов приведет к большему приращению целевой функции. Приращения целевой функции найдем по формуле 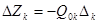 . Вычислим значения параметра
. Вычислим значения параметра 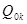 для первого и третьего столбцов по формуле (2.2.5), получим
для первого и третьего столбцов по формуле (2.2.5), получим 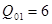 при l=1 (где l – номер строки) и
при l=1 (где l – номер строки) и 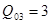 при l=1. находим приращение целевой функции при введении в базис первого вектора
при l=1. находим приращение целевой функции при введении в базис первого вектора 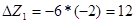 и третьего вектора
и третьего вектора 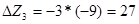 . Следовательно, для наиболее быстрого нахождения оптимального решения необходимо ввести в базис опорного решения вектор
. Следовательно, для наиболее быстрого нахождения оптимального решения необходимо ввести в базис опорного решения вектор 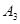 вместо первого вектора базиса
вместо первого вектора базиса 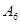 , так как минимум параметра
, так как минимум параметра 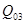 достигается в первой строке (ℓ=1).
достигается в первой строке (ℓ=1).
Далее выполним преобразование Жордана с элементом 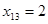 , получим второе опорное решение
, получим второе опорное решение 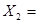 (0, 0, 3, 21, 42, 0) с базисом
(0, 0, 3, 21, 42, 0) с базисом 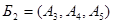 (табл. 2.4.2). Это решение не является оптимальным, так как вектор
(табл. 2.4.2). Это решение не является оптимальным, так как вектор 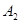 имеет отрицательную оценку
имеет отрицательную оценку 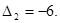 Для улучшения опорного решения необходимо ввести вектор
Для улучшения опорного решения необходимо ввести вектор 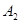 в базис опорного решения.
в базис опорного решения.
Таблица 2.4.2 
| Б | 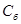 | 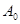 | 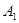 | 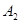 | 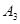 | 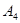 | 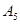 | 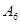 | 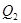 |
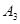 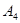 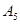 | 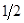 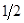 |  -1 -3 -1 -3 | 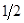 - - 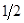 | - - | |||||
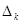 | 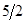 | -6 |
←
Определим номер вектора, выводимого из базиса. Для этого вычислим параметр 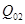 для второго столбца, он равен 7 при ℓ=2. Следовательно, из базиса выводим второй вектор базиса
для второго столбца, он равен 7 при ℓ=2. Следовательно, из базиса выводим второй вектор базиса 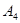 . Выполним преобразование Жордана с элементом
. Выполним преобразование Жордана с элементом 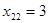 , получим третье опорное решение
, получим третье опорное решение 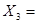 (0, 7, 10, 0, 63, 0) с базисом
(0, 7, 10, 0, 63, 0) с базисом 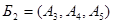 (табл. 2.4.3). Это единственное оптимальное решение, так как для всех векторов, не входящих в базис, оценки разложений по базису опорного решения положительны:
(табл. 2.4.3). Это единственное оптимальное решение, так как для всех векторов, не входящих в базис, оценки разложений по базису опорного решения положительны:
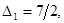
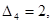
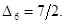
Таблица 2.4.3
| Б | 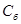 | 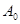 | 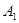 | 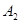 | 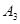 | 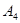 | 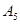 | 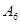 |
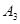 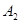 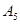 | 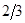 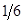 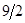 | 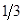 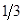 | 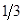 - - 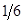 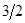 | |||||
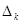 | 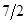 | 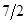 |
О т в е т: max Z(X)=201 при 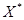 =(0, 7, 10, 0, 63).
=(0, 7, 10, 0, 63).