ГЛАВА 1. Основы теории чисел
А.В. Рожков
О.В. Ниссенбаум
Теоретико-числовые методы в криптографии
Учебное пособие
Тюмень 2007
Аннотация.
Рассмотрены теоретико-числовые и алгебраические основы криптографии, криптографические алгоритмы, построенные на теоретико-числовых и теоретико-сложностных проблемах, такие как RSA, Диффи-Хеллмана, Эль-Гамаля. Рассмотрена проблема генерации простых чисел, приведены вероятностные тесты на простоту и алгоритмы генерации доказуемо простых чисел с математическим обоснованием. В третьей главе приведены алгоритмы, криптоанализа асимметричных криптосистем – алгоритмы факторизации и дискретного логарифмирования – с оценками сложности. Изложение сопровождается примерами. В пособие включены также рабочая программа по дисциплине «Теоретико-числовые методы в криптографии» для студентов специальности «Компьютерная безопасность» ТюмГУ, и задания для самостоятельного выполнения с ответами к ним.
ПРЕДИСЛОВИЕ
Современная криптография в значительной мере использует результаты таких дисциплин как алгебра, теория чисел, теория сложности. Студентам, изучающим криптографию всерьез, необходимо знание ее математических основ, поскольку ничто так не помогает знанию как понимание, а понимание алгоритмов криптографии и криптоанализа невозможно без понимания идей, которые в них заложены.
Предлагаемое учебное пособие базируется на курсе лекций, читаемом авторами в Тюменском государственном университете студентам специальности «Компьютерная безопасность». По окончании обучения студенты этой специальности получают квалификацию «математик», поэтому в этой книге математические факты даются последовательно, с доказательствами настолько строгими и подробными, насколько это позволяет семестровый курс. Однако для того, чтобы читать и понимать это пособие, достаточно знаний математики в объеме, даваемом в технических вузах.
В первой главе содержатся основы теории чисел и криптографические алгоритмы, базирующиеся на теоретико-числовых принципах. Читателю, знакомому с теорией чисел, можно ограничиться чтением шестого и седьмого пунктов из §3, и продолжить чтение начиная с §5. Указанные разделы содержат описания вероятностных тестов на простоту, криптосистем, основанных на теоретико-числовых принципах (таких как RSA, Диффи-Хеллмана), методы построения доказуемо простых чисел. Описания криптосистем сопровождаются доказательствами их стойкости.
Вторая глава посвящена алгебраическим основам теории чисел и таким алгебраическим структурам как кольца многочленов. На кольцах и полях многочленов построены некоторые криптосистемы, в частности AES.
В третьей главе описываются алгоритмы криптоанализа двухключевых криптосистем – алгоритмы факторизации и дискретного логарифмирования. Глава предваряется параграфом, информирующем об основах теории сложности, и для каждого алгоритма из третьей главы приведена оценка сложности. Для всех описанных алгоритмов приведены примеры.
В разделе «Задачи и упражнения» приведены задачи, решение которых поможет закрепить изученный теоретический материал. Примеры решения подобных задач читатель может найти в тексте пособия в соответствующем разделе. Ответы к задачам приведены в конце раздела.
В Приложении 1 приведена таблица простых чисел и порождающих элементов циклических групп целых чисел, им соответствующих.
Приложение 2 представляет собой рабочую программу курса «Теоретико-числовые методы в криптографии», читаемого студентам специальности 090102 «Компьютерная безопасность» в Тюменском государственном университете и включает в себя в том числе вопросы к экзамену.
ВВЕДЕНИЕ
Криптография, или тайнопись, известна с незапамятных времен. Нужда в ней возникала всякий раз, когда людям приходило в голову, что-либо скрыть. От противников, обычно, скрывали военные или государственные секреты, а от непосвященных тайные истины и обряды.
Криптографию часто путают с ее сестрой – теорией кодирования. Если вы, просматривая страницу Интернета, случайно, поставите в браузере какой-нибудь экзотический шрифт, то на экране увидите знаменитые «кракозябры», выглядящие как шифртекст. Однако это никакая не криптография. Тот, кто узнает, что означает каждый из экзотических символов, тоже сможет читать «шифртекст» так же как и вы.
Кодирование можно использовать для сокрытия тайны сообщения, но очень ограниченное время, пока способ кодирования не станет общеизвестным. В кодировании сокрытие информации обеспечивается секретностью алгоритма кодирования. В криптографии же тайна обеспечивается секретностью некоторого параметра алгоритма, называемого ключом. Этот параметр может изменяться и его всегда нужно держать в секрете.
Поскольку шифровать приходится тест, звук, изображение, а не просто набор цифр и символов, то, кажется, что чистая математика, а тем более ее самый абстрактный раздел теория чисел, в этом деле может помочь очень мало. К счастью для математиков, и, к сожалению, для потребителей, это совсем не так. В конечном счете, все сводится к математике, к алгебре, к теории чисел.
Представьте себе огромный корабль, перевозящий товары и пассажиров. В нем много всякой всячины, но главное его предназначение – это доставка груза в порт назначения. Корабль перемещается силой винтов, винты вращаются двигателем, а все в движение приводит микровзрыв в маленьком пространстве в головке цилиндра двигателя – это истинное сердце корабля.
Криптографическая система тот же корабль. В ней есть аппаратная часть – шифраторы, компьютеры, вспомогательное оборудование, например, перекодирующее, изображение с видеокамеры в поток бит для шифратора. Программная часть – операционные системы, драйвера, прикладные и сервисные программы. Команда крипто корабля – шифровальщики, администраторы, агенты, охранники, аудиторы, программисты, пользователи и т.д. И все это нужно для того, чтобы крипто контроллер, в который на аппаратном уровне вшит математический алгоритм, выполнил преобразование, переводящее один набор бит в другой.
Конечно, для большинства пользователей не обязательно знать, что именно вшито в этот крипто чип, какие операции запрограммированы в крипто библиотеке Windows или Unix. Но профессиональные защитники информации, конечно, должны об этом иметь представление. Если продолжить сравнение с кораблем. Не обязательно знать всю теорию двигателя внутреннего сгорания, но нужно понимать на каком горючем он работает, для чего нужен карбюратор, и почему под выхлопной трубой плохо дышится.
Все современные крипто алгоритмы используют важные понятия алгебры – векторные пространства, линейные преобразования, неприводимые многочлены, конечные поля, расширения полей и колец, конечные группы, перестановки, эллиптические кривые, признаки простоты простых чисел и т.д.
Чтобы не быть голословным, перечислим понятия, используемые в алгоритме цифровой подписи - основы товарно-денежных отношений в Интернете. Это поле Галуа, эллиптическая кривая над конечным полем, примитивный элемент поля, порождающий элемент группы, простые числа. К обсуждению этих важных алгебраических понятий мы и приступаем.
Главная цель этого обсуждения - показать, как вся теоретико-числовая техника работает в криптографии. Формальности можно уточнить в любом из классических учебников по алгебре и теории чисел. Часть из них приведена в списке литературы.
По поводу строгости в математике всегда велись споры. Грандиозная попытка изложить всю математику на основе аксиом была предпринята Н.Бурбаки во Франции в середине прошлого века. Было написано несколько десятков томов, но проект остался незавершенным. Изучать математику по Бурбаки совершенно невозможно. Но как справочное пособие для людей, уже знающих предмет, она очень полезна.
ГЛАВА 1. Основы теории чисел.
Теория делимости.
Открытие натуральных чисел было одним из величайших интеллектуальных достижений человечества. Что общего между тремя мамонтами, тремя звездами и тремя вздохами отвергнутого влюбленного? С точки зрения потребительских качеств ничего. Мамонт – это еда, вот она здесь у входа в пещеру, от нее зависит жизнь племени. Звезды в небе, их не потрогаешь, ночью их видно, а днем нет. Вздох вообще нечто не совсем материальное, отдельно от человека не существующее.
Очень не скоро было замечено, что общее между разными предметами и событиями то, что при их перечислении нужно загнуть одно и то же число пальцев на руке, в нашем примере три. Кстати, и до сих пор, (вспомните золотое детство), обучаясь счету, малыши загибают пальцы. С пальцами же связано и возникновение десятичной системы счисления. Кстати, если бы 400 млн. лет назад на берег из океана выползла не пятипалая двоякодышащая рыба, потомками которой мы являемся, а, например, с четырьмя лучами на плавнике, то победила бы восьмеричная система счисления.
Как бы то ни было, человечеством была освоена главная идея, лежащая в основе понятия о натуральном числе. Идея взаимно-однозначного соответствия или биекции между элементами разных множеств.
Множество натуральных чисел сейчас принято обозначать ажурной заглавной буквой N.Натуральными числами являются {1,2,3,…}. Понятие о нуле возникло гораздо позже, чем об остальных целых числах. Ноль обозначает ничто, однако 0 – вполне осязаемый символ ничем не хуже чем 1 или 5. Ноль – это нечто, а обозначает он ничто. Нечто обозначающее ничто – это уже шаг к раздвоению личности и он нормальным людям дался нелегко. Отрицательные числа (понимаемые как долг, как недостача) вошли в сознание людей гораздо проще, так же как и дроби, понимаемые как часть единого целого.
Основные понятия и теоремы.
Предмет теории чисел – целые числа и их свойства.
Множество целых чисел обозначается символом Z, символом Z+ обозначается множество целых положительных чисел, символом N– множество натуральных чисел. Латинскими малыми буквами здесь и далее будем обозначать целые числа.
Заметим, что 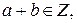
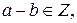
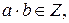
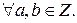
То есть как сумма, так и произведение целых чисел также являются целыми числами. Частное двух целых чисел не всегда является целым числом.
Если 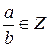 , (b≠0)
, (b≠0) 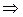
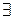
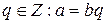 ,
, 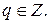 Тогда говорят, что а делится на b, или b делит а, и пишут b\a. Тогда а называем кратным числа b, а b – делителем числа а.
Тогда говорят, что а делится на b, или b делит а, и пишут b\a. Тогда а называем кратным числа b, а b – делителем числа а.
Справедливы следующие
Теоремы:
(1) m\a, b\m 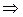 b\a.
b\a.
Доказательство:
m\a  a=ma1;
a=ma1;
b\m 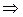 m=bm1
m=bm1 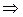 a=bm1a1. Обозначив b1=a1m1, получим a=bb1, причем
a=bm1a1. Обозначив b1=a1m1, получим a=bb1, причем 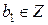
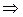 b\a.
b\a.
□
(2) Если в равенстве вида k+l+…+n=p+q+…+s относительно всех членов кроме одного известно, что они кратны b, то и один оставшийся член тоже кратен b.
Доказательство:
Не нарушая общности, предположим, что таким членом (относительно кратности которого числу b ничего не известно) является k.
Тогда 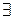 l1, …, n1, p1, q1, …, s1: l=bl1,…, n=bn1, p=bp1, q=bq1, …, s=bs1.
l1, …, n1, p1, q1, …, s1: l=bl1,…, n=bn1, p=bp1, q=bq1, …, s=bs1.
Тогда k=p+q+…+s–l–…–n=bp1+bq1+…+bs1–bl1–…–bn1=b(p1+q1+…+s1–l1–…–n1)
Обозначим k1= p1+q1+…+s1–l1–…–n1. Очевидно, k1 – целое число, причем k=bk1 Тогда, по определению делимости, b\k.
□
Кроме того, очевидны следующие свойства:
1) 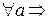 a\0, 1\a, a\a.
a\0, 1\a, a\a.
2) a\b, b\a  a=±b.
a=±b.
3) a\b, a\c 
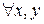 a\(bx+cy).
a\(bx+cy).
(Доказательство св-ва 3: b=ab1, c=ac1  bx+cy=ab1x+ac1y=a(b1x+c1y))
bx+cy=ab1x+ac1y=a(b1x+c1y))
