Ряд Тейлора. Ряд Маклорена

Рядом Тейлора, расположенным по степеням (x – x₀), для функции f(x) называется степенной ряд

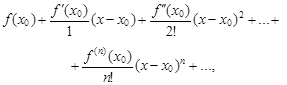(13)

где 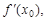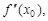…, … 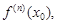– производные функции f(x) в точке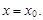

При x = 0 ряд Тейлора, расположенный по степеням х, имеет вид

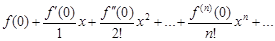. (14)

Формула (14) представляет частный случай формулы Тейлора (13). Формула (14) называется формулой Маклорена.

Пример 18.Для функции f(x) 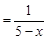составить ряд Тейлора, расположенный по степеням (x – 2).

Решение

Найдем значения функции f(x) и ее последовательных производных 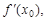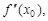…, 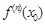при x₀ = 2:

1) значение функции f(x₀) при x₀ = 2: f(x₀) = f(2)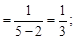

2) производную первого порядка: 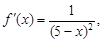ее значение при x₀ = 2: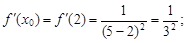

3) производную второго порядка: 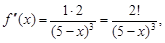ее значение при x₀ = 2: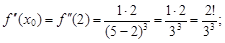

4) производную третьего порядка: 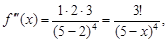ее значение при x₀ = 2: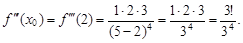

Тогда производная п-го порядка будет равна: 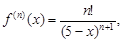а ее значение при x₀ = 2: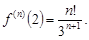

Подставив x₀ = 2, а также найденные значения функции f(x) и производных f ¢(x₀), 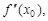…, f ⁽ⁿ⁾(x₀) при x₀ = 2 в формулу (13), получим

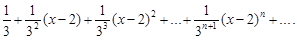
Пример 19.Для функции f(x) 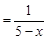составить ряд Тейлора, расположенный по степеням х (т. е. составить ряд Маклорена).

Решение

Найдем значения функции f(x) и ее последовательных производных 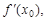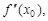…, 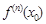при x₀ = 0:

1) значение функции 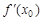при x₀ = 0: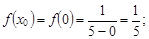

2) производную первого порядка: 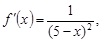ее значение при x₀ = 0: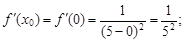

3) производную второго порядка: 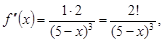ее значение при x₀ = 0: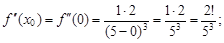

4) производную третьего порядка: 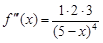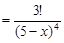, ее значение при x₀ = 0: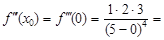

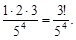
Тогда производная п-го порядка будет равна: 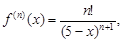а ее значение при x₀ = 0: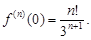

Подставив найденные значения функции f(x) и производных 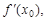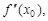…, 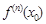при x₀ = 0 в формулу (14), получим

.

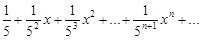Пример 20.Для функции f(x) 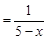составить ряд Тейлора, расположенный по степеням (x – 5).

Решение

У функции f(x) 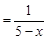нет ряда Тейлора, расположенного по степеням (x – 5), так как функция f(x) 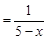в точке x = 5 не определена.

Тест 28. Для функции f(x) 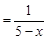ряд Тейлора, расположенный по степеням (x – 5), имеет вид:

1) ;

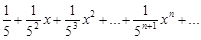2) у данной функции нет ряда, расположенного по степеням (x – 5);

3) ;

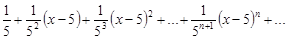4) .

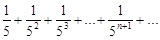Тест 29.Ряд Маклорена получается из ряда Тейлора:

1) при x = 1;

2) при x = –1;

3) при x = 0;

4) при x = 5;

5) при x = 2.

Ответы на тестовые задания

Номер теста
Правильный ответ

Номер теста
Правильный ответ

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Кудрявцев, В. А. Краткий курс высшей математики : учеб. пособие / В. А. Кудрявцев, Б. П. Демидович. – М. : Наука, 1989. – 656 с.

Марков, Л. Н. Высшая математика. Элементы линейной и векторной алгебры. Основы аналитической геометрии : учеб. пособие для вузов / Л. Н. Марков, Г. П. Размыслович. – Минск : Амалфея, 1999. – 208 с.

Минюк, С. А. Высшая математика : учеб. пособие для вузов /
С. А. Минюк, Е. А. Ровба. – Гродно : ГрГУ, 2000. – 394 с.

Шипачев, В. С. Высшая математика : учеб. / В. С. Шипачев ; под ред. А. Н. Тихонова. – М. : Высш. шк., 1990. – 479 с.

Яблонский, А. И. Высшая математика. Общий курс : учеб. /
А. И. Яблонский [и др.] ; под общ. ред. С. А. Самаля. – 2-е изд., перераб. – Минск : Выш. шк., 2000. – 351 с.

СОДЕРЖАНИЕ

Пояснительная записка...................................................................... 3

Программа курса............................................................................... 4

Раздел I. Линейная алгебра и аналитическая геометрия........... 8

1.1. Аналитическая геометрия на плоскости................................... 8

1.2. Векторная алгебра.................................................................... 29

1.3. Элементы аналитической геометрии в пространстве............. 37

1.4. Матрицы.................................................................................... 46

1.5. Системы линейных уравнений и неравенств........................... 69

1.6. Комплексные числа.................................................................. 80

Раздел II. Математический анализ и дифференциальные
уравнения............................................................................ 91

2.1. Числовая последовательность и ее предел............................. 91

2.2. Предел функции одной переменной...................................... 103

2.3. Непрерывные функции одной переменной........................... 120

2.4. Производная и дифференциал функции одной переменной 128

2.5. Основные теоремы о дифференцируемых функциях........... 138

2.6. Приложения дифференциального исчисления...................... 148

2.7. Функции нескольких переменных......................................... 161

2.8. Первообразная и неопределенный интеграл......................... 193

2.9. Определенный интеграл......................................................... 200

2.10. Кратные интегралы............................................................... 210

2.11. Обыкновенные дифференциальные уравнения................... 221

2.12. Ряды....................................................................................... 241

Список рекомендуемой литературы............................................. 266

Учебное издание

ВЫСШАЯ
МАТЕМАТИКА

ОБЩИЙ КУРС

Пособие

по подготовке к тестированию для студентов
заочной формы получения высшего образования
экономических специальностей

Авторы-составители:

Авдашкова Людмила Павловна

Воробей Людмила Александровна

Грибовская Марал Атаевна и др.

Редакторы И. А. Михайлова

Технический редактор И. А. Козлова

Компьютерная верстка Н. Н. Короедова

Подписано в печать 05.10.11. Бумага типографская № 1.

Формат 60 ´ 84 ¹/₁₆. Гарнитура Таймс. Ризография.

Усл. печ. л. 15,58. Уч.-изд. л. 15,85. Тираж 300 экз.

Заказ №

Учреждение образования

«Белорусский торгово-экономический

университет потребительской кооперации».

246029, г. Гомель, просп. Октября, 50.

ЛИ № 02330/0494302 от 04.03.2009 г.

Отпечатано в учреждении образования

«Белорусский торгово-экономический

университет потребительской кооперации».

246029, г. Гомель, просп. Октября, 50.