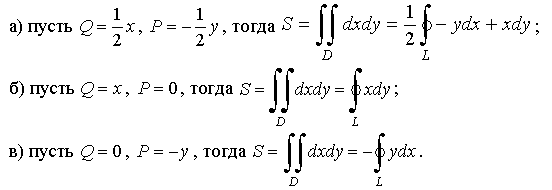Вычисление криволинейного интеграла первого рода

Пусть гладкая дуга АВ задана параметрически уравнениями: x=x(t), y=y(t), z=z(t),где α ≤ t ≤ β.

Кроме того, на этой дуге определены и непрерывны функции f(x,y,z), P(x,y,z), Q(x,y,z), R(x,y,z), тогда криволинейные интегралы могут быть вычислены следующим образом:

а) криволинейный интеграл 1-го рода: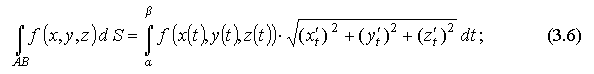

б) криволинейный интеграл 2-го рода: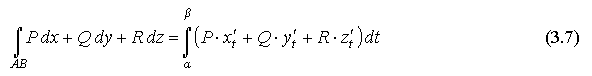

***********************

Криволинейный интеграл второго рода, его свойства.

Пусть АВ - дуга гладкой кривой (рис. 3.2), на которой определена и непрерывна векторная функция

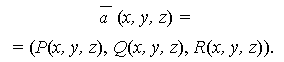
Выполним следующие действия:

1) разобьем дугу АВ произвольным образом в направлении от А к В с помощью точек М_i (i = 1, ..., n) на n частичных дуг:Δl₁, Δl₂, ..., Δl_i, ..., Δl_n.

Пусть λ_n- наибольшая из длин частичных дуг. Понятно, что если λ_n → 0, то n → ∞.

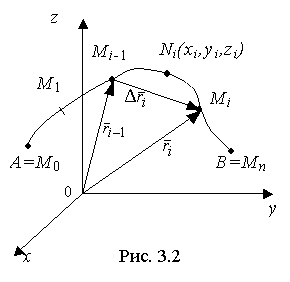
2) выберем произвольным образом точки N_i(x_i, y_i, z_i) 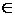Δl_i (i=1,...,n);

3) организуем векторы и 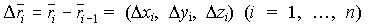вычислим значения векторной функции 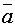в точках N_i (i = 1, ..., n), т. е. 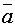(N_i)=(P(N_i), Q(N_i), R(N_i));

4) составим интегральную сумму вида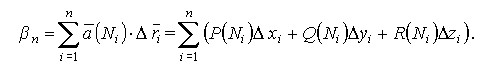

Определение

Конечный предел интегральной суммы β_n при λ_n → 0, если он существует и не зависит от способа деления дуги АВ на частичные дуги и от способа выбора точек N_i 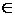Δ_i (i=1,...,n), называется криволинейным интегралом второго рода (по координатам) от векторной функции 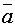=(P,Q,R) по дуге АВ в направлении от А к B и обозначается:

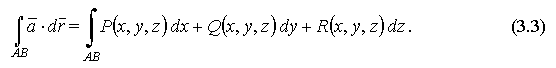
Геометрические и физические приложения интеграла (3.3) разнообразны, некоторые из них будут упомянуты в дальнейшем.

Из построения интеграла (3.3) очевидно, что при изменении направления обхода дуги АВ интеграл меняет знак, т. е.

Об условиях существования интеграла (3.3) говорит следующая теорема.

Теорема

Если дуга АВ гладкая, и функция 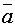= (P,Q,R) непрерывна на ней, то интеграл (3.3) существует.

Можно сформулировать более сильные условия существования криволинейного интеграла по координатам.

********************************

Вычисление криволинейного интеграла второго рода.

Пусть l — гладкая, спрямляемая кривая, заданная параметрически. Пусть функция 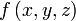определена и интегрируема вдоль кривой l в смысле криволинейного интеграла второго рода. Тогда

,

,

.

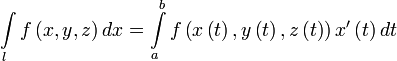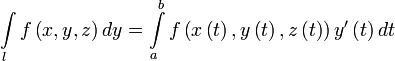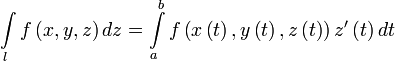Если обозначить за 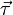касательный вектор к кривой l, то нетрудно показать, что

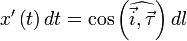
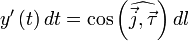
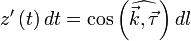
Формула Грина

Формула Грина связывает двойной интеграл по плоской области с криволинейным интегралом по контуру этой области.

Пусть функции P(x,y), Q(x,y), P'_y(х,у), Q'_x(х,у) непрерывны в замкнутой области D, ограниченной контуром L (рис. 3.6).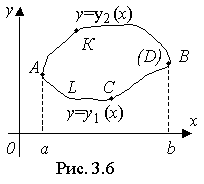

Пусть контур L, кроме того, пересекается прямыми, параллельными осям координат, не более чем в двух точках.

Пусть уравнение АСВ есть y = y₁(x) при a ≤ x ≤ b, и уравнение АКВ есть y = y₂(x)при a ≤ x ≤ b.

Преобразуем двойной интеграл

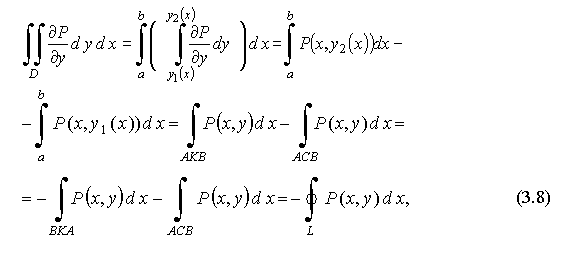здесь символ 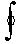означает криволинейный интеграл по замкнутому контуру L.

Аналогично получается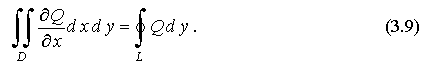
Вычитая из формулы (3.9) формулу (3.8), получаем формулу Грина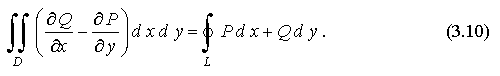

В формулах (3.8), (3.9) и (3.10) направление обхода контура - положительное (против часовой стрелки), т. е. область D при движении по контуру L всё время остается слева.
С помощью формулы Грина (3.10) можно получить выражения площади плоской фигуры через криволинейный интеграл по контуру этой фигуры.

Для этого достаточно подобрать P(x,y) и Q(х,y) такими, чтобы в области D выполнялось условие ,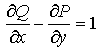

тогда двойной интеграл в формуле (3.10) будет давать величину S площади области D.

Например: