ТЕМА «Комплексные числа»
Задания для подготовки к экзамену 2 семестр
Экзаменационные вопросы
Производная (повторение 1 семестра)
1. Понятие производной, ее геометрический и механический смысл.
2. Непрерывность и дифференцируемость функции.
3. Производная постоянной, суммы, произведения и частного.
4. Производная сложной функции.
5. Производная обратной функции.
6. Производные основных элементарных функций.
7. Производная функции, заданной параметрически.
8. Производная функции, заданной неявно.
9. Логарифмическое дифференцирование.
10. Дифференциал функции, его свойства.
11. Производные высших порядков.
12. Дифференциалы высших порядков.
14. Теоремы о среднем.
15. Правило Лопиталя.
16. Формула Тейлора.
17. Признаки возрастания и убывания функции.
18. Экстремум функции.
19. Выпуклость и вогнутость функции, точки перегиба.
20. Асимптоты.
21. Общая схема исследования функции и построения ее графика.
22. Наибольшее и наименьшее значения функции на отрезке.
Функции нескольких переменных.
23. Понятие функции нескольких переменных. Область определения.
24. Предел и непрерывность функции нескольких переменных.
25. Частные производные и дифференциал.
26. Частные производные и дифференциалы высших порядков.
27. Дифференцирование сложной функции.
28. Дифференцирование неявной функции.
29. Экстремум функции двух переменных.
30. Скалярное поле.
31. Производная по направлению.
32. Градиент скалярного поля.
33. Касательная плоскость и нормаль к поверхности.
34. Наименьшее и наибольшее значения функции нескольких переменных в ограниченной замкнутой области.
Интегрирование функций одной переменной (неопределенный и определенный интегралы)
35. Понятие первообразной. Неопределенный интеграл, его свойства.
36. Таблица основных интегралов.
37. Замена переменной и интегрирование по частям.
38. Интегрирование тригонометрических функций.
39. Интегрирование рациональных функций.
40. Определенный интеграл как предел интегральных сумм, его свойства.
41. Формула Ньютона-Лейбница.
42. Замена переменной и интегрирование по частям в определенном интеграле.
43. Несобственные интегралы.
Дифференциальные уравнения
44. Дифференциальные уравнения 1-го порядка (ДУ-1).
45. Теорема Коши существования и единственности решения ДУ-1.
46. Уравнения с разделяющимися переменными.
47. Однородные уравнения.
48. Линейные уравнения и уравнения Бернулли.
49. Уравнения в полных дифференциалах.
50. ДУ высших порядков
51. ДУ высших порядков, допускающие понижение порядка.
52. Линейные однородные дифференциальные уравнения 2-го порядка (ЛОДУ-2). Структура общего решения.
53. Линейные неоднородные дифференциальные уравнения 2-го порядка (ЛНДУ-2). Структура общего решения.
54. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Построение общего решения ЛОДУ.
55. Метод вариации произвольных постоянных для решения ЛНДУ
56. Метод неопределенных коэффициентов для решения ЛНДУ.
57. Системы линейных дифференциальных уравнений.
58. Применение теории ЛНДУ к изучению колебательных движений: свободные и вынужденные колебания.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ 2 СЕМЕСТР
ТЕМА «Комплексные числа»
| 1. | Найти модуль и аргумент числа, записать его в тригонометрической и экспоненциальной форме, изобразить на комплексной плоскости: 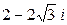 . . | |
| 2. | Найти 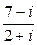 | |
| 3. | Вычислить 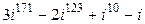 | |
| 4. | Вычислить 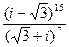 . . | |
| 5. | Вычислить и изобразить на комплексной плоскости: 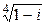 . . | |
ТЕМА «Функции нескольких переменных» 1. Для заданной функции найти все частные производные первого порядка: а) 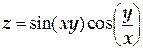 ; б) ; б) 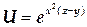 ; 2. Для заданной функции найти требуемые частные и смешанные производные: ; 2. Для заданной функции найти требуемые частные и смешанные производные: 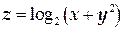 ; ; 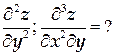 3. Проверить, что функция 3. Проверить, что функция 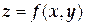 удовлетворяет заданному уравнению: удовлетворяет заданному уравнению: 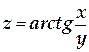 ; ; 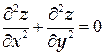 4. Найти производные неявно заданной функции: а) 4. Найти производные неявно заданной функции: а) 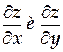 ; б) ; б) 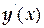 1. 1. 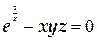 ; 2. ; 2. 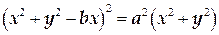 5. Найти градиент функции 5. Найти градиент функции 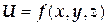 в точке в точке 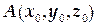 и вычислить его модуль и вычислить его модуль 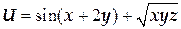 ; ; 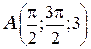 6. Для функции 6. Для функции 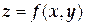 в точке в точке 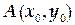 вычислить градиент и производную в направлении вектора вычислить градиент и производную в направлении вектора 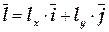 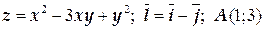 7. Найти полный дифференциал функции: а) 7. Найти полный дифференциал функции: а) 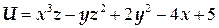 ; б) ; б) 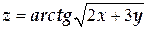 8. С помощью полного дифференциала найти приближенное значение функции: 8. С помощью полного дифференциала найти приближенное значение функции: 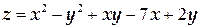 при при 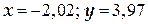 9. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке 9. Найти уравнения касательной плоскости и нормали к заданной поверхности в указанной точке 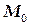 : : 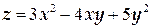 ; ; 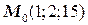 10. Исследовать на экстремум функцию 10. Исследовать на экстремум функцию 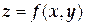 , , 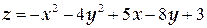 1. Вычислить частные производные 1. Вычислить частные производные 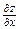 и и 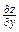 для функции для функции 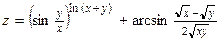 . 2. Вычислить все частные производные второго порядка для функции: . 2. Вычислить все частные производные второго порядка для функции: 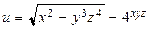 . 3. Вычислить полный дифференциал для функции . 3. Вычислить полный дифференциал для функции 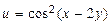 . 4. Функция . 4. Функция 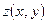 задана неявно: задана неявно: 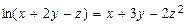 . Вычислить частные производные . Вычислить частные производные 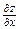 и и 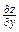 . 5. Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением . 5. Написать уравнения касательной плоскости и нормали к поверхности, заданной уравнением 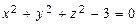 в точке в точке 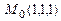 . 6. Исследовать функцию на экстремум . 6. Исследовать функцию на экстремум 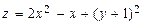 . ТЕМА «Неопределенный интеграл» . ТЕМА «Неопределенный интеграл» |
| 1. | 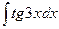 | 21. | 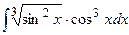 |
| 2. | 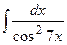 | 22. | 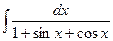 |
| 3. | 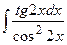 | 23. | 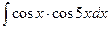 |
| 4. | 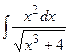 | 24. | 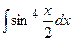 |
| 5. | 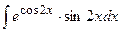 | 25. | 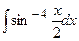 |
| 6. | 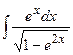 | 26. | 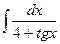 |
| 7. | 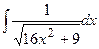 | 27. | 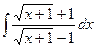 |
| 8. | 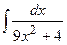 | 28. | 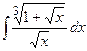 |
| 9. | 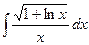 | 29. | 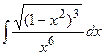 |
| 10. | 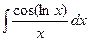 | 30.  | 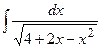 |
| 11. | 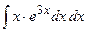 | 31. | 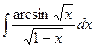 |
| 12. | 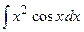 | 32. | 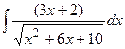 |
| 13. | 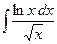 | 33. | 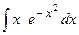 |
| 14. | 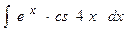 | 34. | 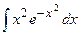 |
| 15. | 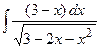 | 35. | 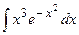 |
| 16. | 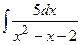 | 36. | 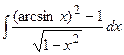 |
| 17. | 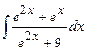 | 37. | 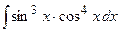 |
| 18. | 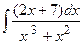 | 38. | 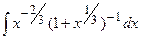 |
| 19. | 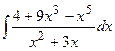 | 39. | 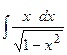 |
| 20. | 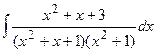 | 40. | 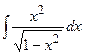 |
