Геометрические и физические приложения о и

y y = f(x)

Dx_i

a b x

Определение: Длиной дуги называется предел периметра вписанной в нее ломанной, если длина максимал. ломаной стремится к 0. Если предел конечен, то дуга – спрямляемая.

Длина ломаной линии, которая соответствует дуге, может быть найдена как .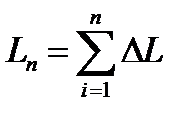

Тогда длина дуги равна .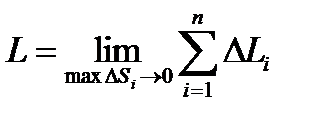

Из геометрических соображений: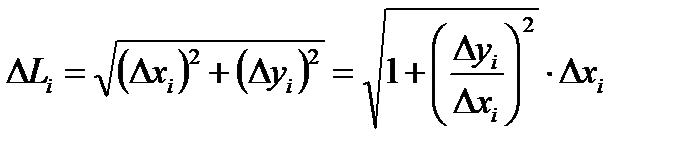

В то же время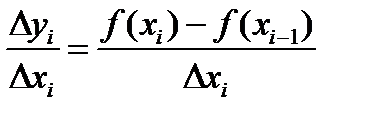

Тогда можно показать, что 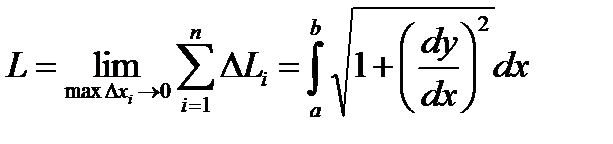Т.е.

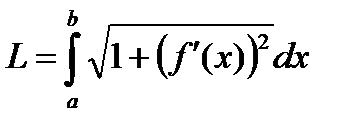
Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной функции, получаем 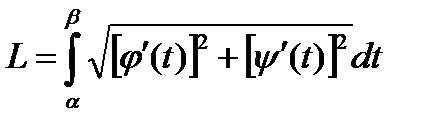, где х = j(t) и у = y(t).

Если задана пространственная кривая, и х = j(t), у = y(t) и z = Z(t), то

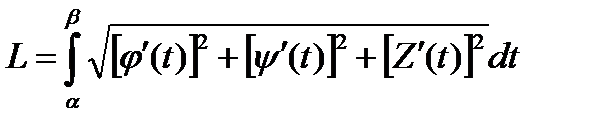
если кривая задана в полярных координатах, то 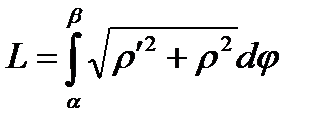, r = f(j).

Диф-л дуги: L’(x) = dL/dx = a/√1+f ’²(x)

рис. dL = (a/√(1+f ’²(x)))*dx = √dx²+dy

dL² = dx²+dy²

13. Нес инт с бескон пред инт-я. Н и от ннеогран ф-й

Пусть функция f(x) определена и непрерывна на интервале [a, ¥). Тогда она непрерывна на любом отрезке [a, b].

Определение: Если существует конечный предел 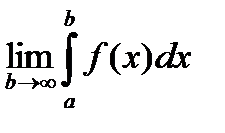, то этот предел называется несобственным интегралом от функции f(x) на интервале [a, ¥).

Обозначение: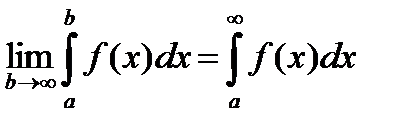

Если этот предел существуетиконечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Аналогичные рассуждения можно привести для несобственных интегралов вида:

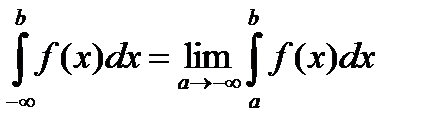
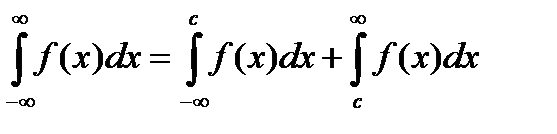
Конечно, эти утверждения справедливы, если входящие в них интегралы существуют.

Пример.

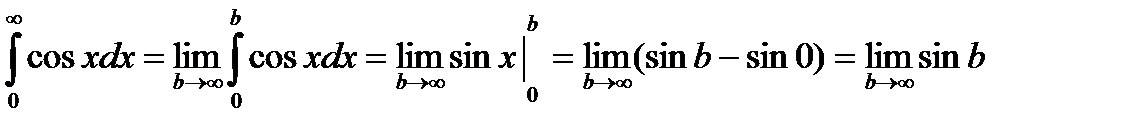- не существует.

Несобственный интеграл расходится.

Теорема: Если для всех х (x ³ a) выполняется условие 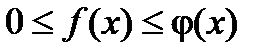и интеграл 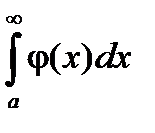сходится, то 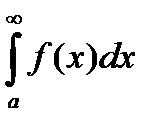тоже сходится и 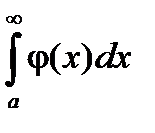³ .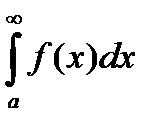

Теорема: Если для всех х (x ³ a) выполняется условие 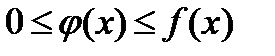и интеграл 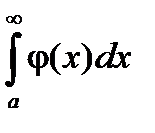расходится, то 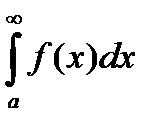тоже расходится.

Теорема: Если 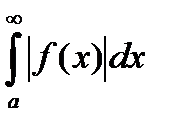сходится, то сходится и интеграл .

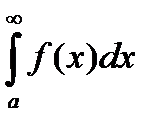В этом случае интеграл 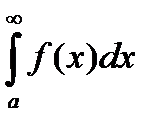называется абсолютно сходящимся.

13-14. Нес инт с бескон пред инт-я. Н и от ннеогран ф-й

Пусть ф-ия f(x) определена на [a;b) интегрируема на любом промежутке [a;b- 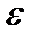] и кроме того 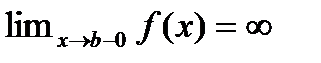. Рассмотрим 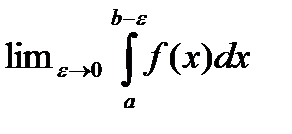Если указанный предел сущ то говорят что этот предел наз несобственным Интеграл от ф-ии f(x) (несобственным интегралом второго рода) И обознач 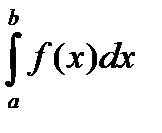анологично если т. a особенная и 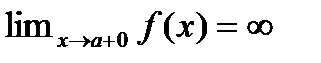На промежутке 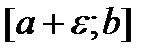ф-ия интегрируема, то несобственный интеграл вводится так 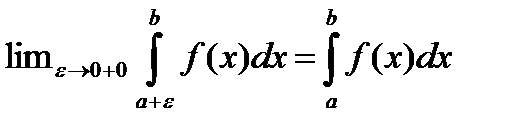. Если особой точкой является внутренняя точка отрезка [a;b) то под несобственным интегралом понимается 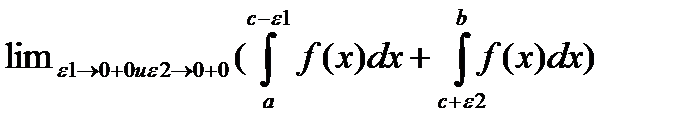. Подчеркнем что в 3-ем случае 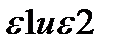стремятся к нулю независимо друг от друга. Если указанные пределы сущ то несобственные интегралы наз сходящимися а если равны бесконечности или не сущ то эти интегралы наз росходящимися в случае если f(x) неограниченная ф-ия то можно дать геометрическую интерпритацию несобсятвеных интегралов второго рода.

критерии Коши и признаки сравнения. Пусть С- внутренняя точка (особоя) для того чтобы несобственный 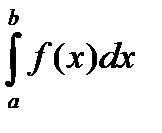был сходящимся необходимо и достаточно чтобы для любого 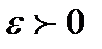существовала такая 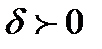чтобы для любых четырех отрицательных чисел 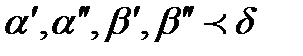выполнялось 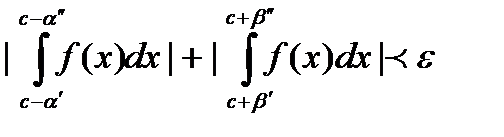. Признак сравнения:

Пусть для всех X из облости существования выполняется условие 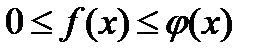тогда и сходимости несобственного интеграла 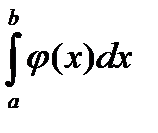вытекает сходимость несобственного интеграла 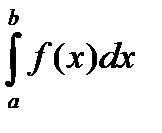. И наоборот из расходимости несобственного интеграла 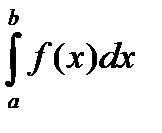следует расходимость несобственнго интеграла .

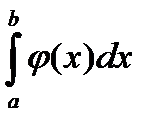Теорема:(предельный признак сходимости): Пусть на отрезке [a;b) f(x) и 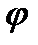(x) знакоположительные ф-ии 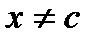. И сущ 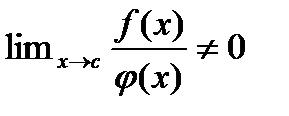тогда в смысле сходимости оба интеграла 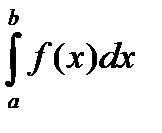и 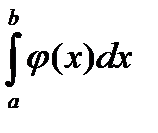ведут себя одинаково т.е. одновременно сходятся и расходятся.

16. Функции нескольких переменных. Предел ФМП. . Частные производные

При рассмотрении фмп ограничимся подробным описанием функций двух переменных,

Опр: Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.

z = f(x, y)

Опр: Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.

Опр: Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Опр: Окрестностью точкиМ₀(х₀, у₀) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию .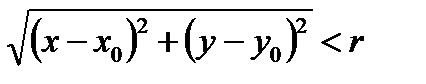

18-20

Опр: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие 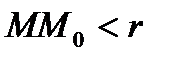также верно и условие .

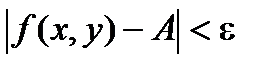Записывают: 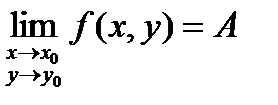Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина D_xz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.

Можно записать 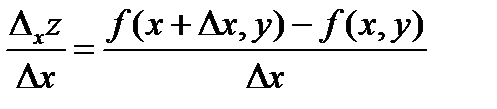. Тогда 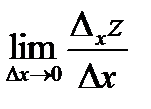называется частной производнойфункции z = f(x, y) по х.

Обозначение: 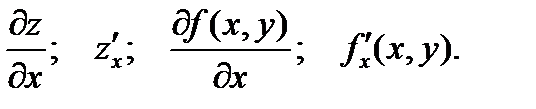частная производная функции по у.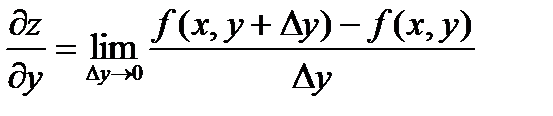

Геометрическим смысломчастной производной (допустим 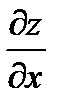) является тангенс угла наклона касательной, проведенной в точке N₀(x₀, y₀, z₀) к сечению поверхности плоскостью у = у₀.

20 Частные производные высших порядков.

Если функция f(x, y) определена в некоторой области D, то ее частные производные 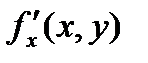и 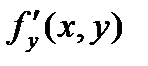тоже будут определены в той же области или ее части.

Будем называть эти производные частными производными первого порядка.

Производные этих функций будут частными производными второго порядка.

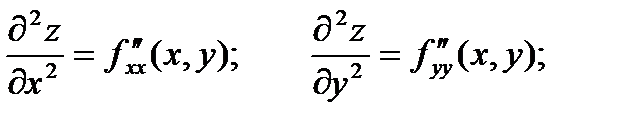
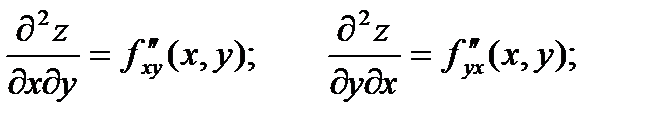
Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

Определение. Частные производные вида 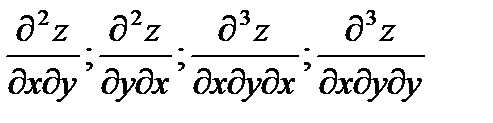и т.д. называются смешанными производными.

Теорема. Если функция f(x, y) и ее частные производные 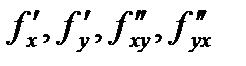определены и непрерывны в точке М(х, у) и ее окрестности, то верно соотношение:

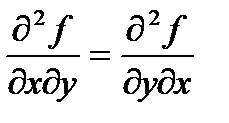. Т.е. частные производные высших порядков не зависят от порядка дифференцирования.