Геометрические и физические приложения

1) Длина кривой: 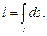2) Масса кривой. Если подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, то массу кривой определяют по формуле: 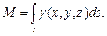3) Моменты кривой l: 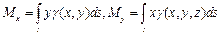- статические моменты плоской кривой l относительно осей Ох и Оу; 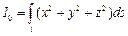- момент инерции пространственной кривой относительно начала координат; 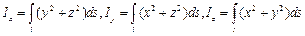- моменты инерции кривой относительно координатных осей.

4) Координаты центра масс кривой вычисляются по формулам: .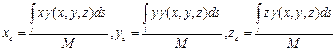

§ 2. Криволинейный интеграл по координатам (второго рода)

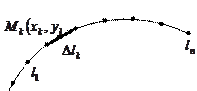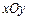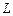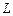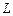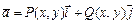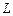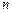Рассмотрим на плоскости ориентированную гладкую дугу (т.е. на дуге указано направление и в каждой точке существует касательная). Пусть на определена и непрерывна вектор-функция . Разобьем дугу на элементарных дуг 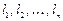и построим векторы 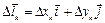, направленные из начала в конец дуги 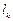. На каждой элементарной дуге 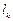выберем произвольную точку 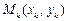и составим сумму скалярных произведений 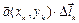: 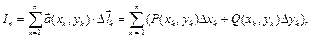называемую 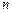-ой интегральной суммой.

Определение. Предел последовательности интегральных сумм 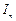при условии, что 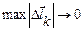, называется криволинейным интегралом по координатам (второго рода) и обозначается .

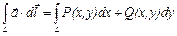Аналогично вводится определение криволинейного интеграла от вектор-функции 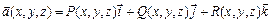, по пространственной дуге : .

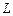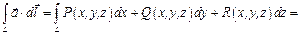
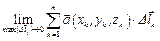Свойства криволинейного интетграла аналогичны свойствам определенного интеграла. В частности, из определения следует, что 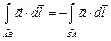, т.е. при изменении направления пути интегрирования криволинейный интеграл меняет знак.

Вычисление криволинейного интеграла сводится к вычислению соответствующего определенного интеграла следующим образом.

1) Если пространственная дуга 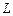задана параметрическими уравнениями 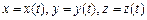, , 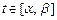то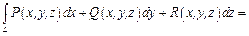

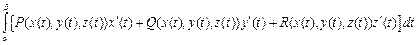
2) Если плоская дуга 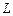задана уравнением 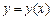, , 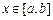то .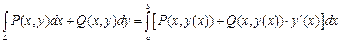

Зам. Если ф-ии 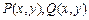непрерывны вместе со своими частными производными в некоторой замкнутой области 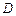с границей 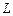, то справедлива формула Грина: 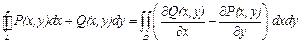, где замк. контур 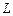обходится против часовой стрелки.

Механический смысл криволинейного интеграла

1) Пусть тело под действием переменной силы 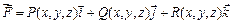движется по дуге кривой 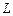. Тогда работа 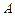этой силы может быть вычислена по формуле .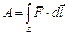

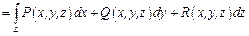2) Рассмотрим непрерывное векторное поле 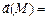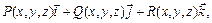определенное в каждой точке гладкой замкнутой кривой 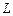. Циркуляцией 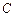векторного поля 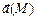вдоль замкнутой кривой 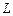называется криволинейный интеграл второго рода 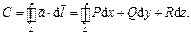В случае, когда векторное поле 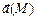является силовым полем, циркуляция дает величину работы этого поля вдоль кривой 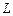. Если кривая 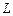лежит в плоскости 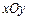, то направление обхода против часовой стрелки считается положительным, а по часовой – отрицательным.

Пример 1.

Найти массу кривой с линейной плотностью 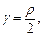заданной в полярных координатах уравнением ρ =4φ, где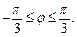

Решение.

Используем формулу (40) с учетом того, что кривая задана в полярных координатах:

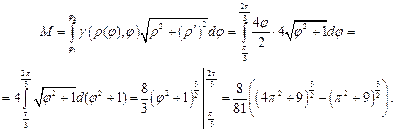
Пример 2.

Вычислить работу векторного поля 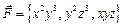вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).

Решение.

Найдем канонические и параметрические уравнения прямой АВ:

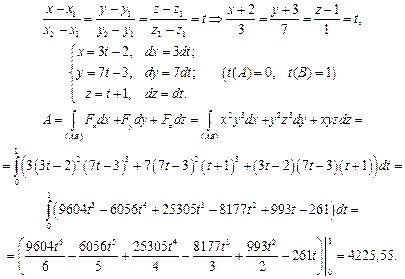
Пример 3. Вычислить 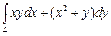, если 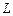1) дуга параболы 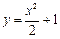, расположенная между точкам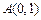и и 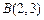; 2) отрезок прямой .

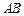Решение. 1) Сведем вычисление криволинейного интеграла к опре­деленному, полагая , , .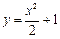

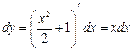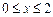Тогда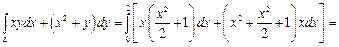

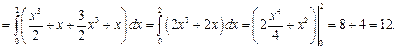
2) Запишем уравнение прямой, проходящей через точк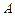и и :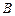

; .

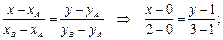
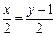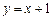Следовательно,

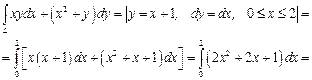
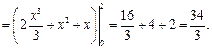
Пример 4. Вычислить работу силового поля 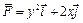при перемещении материальной точки вдоль контура окружности 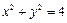, пробегаемой против часовой стрелки.

Решение. Запишем параметрические уравнения окружности: 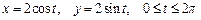(т.к. обход окружности ведется против часовой стрелки). Работу А силы 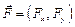найдем по формуле: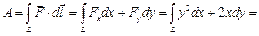

.

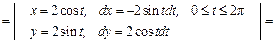
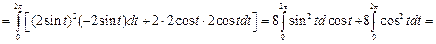
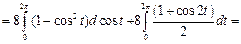
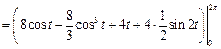
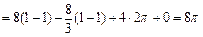Пример 5. Вычислить 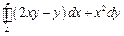, где 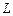– контур тре­угольника 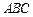с вершинами в точках А(–1, 0), В(0, 2), С(0, 1) (рис.).

Решение. Поскольку контур является замкнутым, применим фор­мулу Грина. В нашем случае

, ,

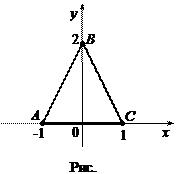
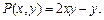
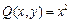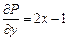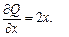
Следовательно, =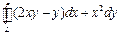

.

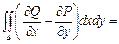
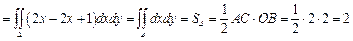Пример 6.Найти функцию 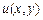по ее полному дифференциалу:

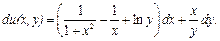
Решение. Воспользуемся первой из формул (12.1), выбрав за на­чальную точку 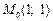. Такой выбор вызван тем, что при 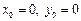функци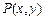и и 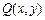не определены. Получим

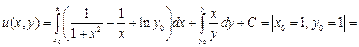
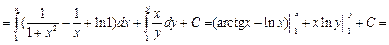
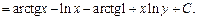
Поскольку 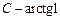также является постоянной, то окончательный ответ можно записать в виде .

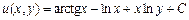Пример 7.Материальная точка массой 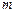движется по эллипсу :

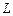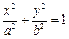в положительном направлении под действием пере-

менной силы 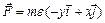, где 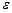– угловое ускорение. Вычислить циркуляцию вектора 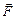вдоль контура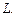

Решение.Запишем параметрические уравнения эллипса

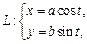
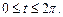
Циркуляция вектора 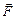вдоль контур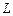а равна

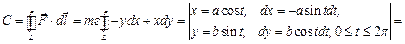
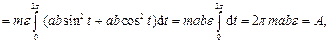
где 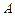– работа силы 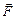вдоль контура .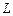