Дифференциальные уравнения первого порядка (общие понятия)
Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную, искомую функцию и производную этой функции. Дифференциальное уравнение первого порядка имеет вид:
F(x, y, y¢ )=0
Условия, заключающиеся в том, что при заданных значениях аргумента значения функции или ее производной должны равняться конкретному числу, называются начальными условиями.
Начальные условия можно записать следующим образом:
y = y0 при x = x0 или y|x=x0 = y0.
Рассматривая выше распад радиоактивного элемента, мы получили дифференциальное уравнение первого порядка
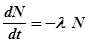 (1)
(1)
т.е. F( t, N, N¢ )=0
Попробуем решить это уравнение. Разделим переменные. Уравнение (1) тогда будет иметь вид:

Проинтегрируем это выражение.

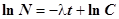 (1а)
(1а)
Замечание: Имея ввиду дальнейшие преобразования, мы обозначили произвольную постоянную через ln C, что вполне допустимо, т.к. ln C (при C¹0) может принимать любые значения от - ¥ до + ¥.
С полученным выражением (1а) проведем несложные алгебраические преобразования

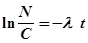
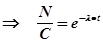
 (2)
(2)
Нетрудно проверить, что полученная функция (2) удовлетворяет уравнению (1), каково бы ни было постоянное число C.
Следовательно, данная совокупность функций N = f (t), является решением дифференциального уравнения.
Определение 13. Общим решением дифференциального уравнения первого порядка называется функция y = j (x, C), которая зависит от произвольного постоянного C и удовлетворяет следующим условиям
1. обращает в тождество дифференциальное уравнение при любом конкретном C;
2. каковы бы ни были начальные условия y = y0 при x = x0 можно найти такое значение C=C0, что функция y = j (x, C0) удовлетворяет данным начальным условиям.
Рассмотрим далее наш пример. Зададим начальные условия, в момент t = 0 - т.е. начало радиоактивного распада, число нераспавшихся атомов было N=N0 . Тогда легко можно найти величину C = C0, соответствующую данным начальным условиям. Подставляя в выражение (2) вместо N, N0, а вместо t нуль, имеем
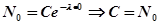
Таким образом, число нераспавшихся атомов зависит от времени по следующему закону

Это выражение есть частное решение дифференциального уравнения.
Определение14. Частным решением дифференциального уравнения называется любая функция y = j (x, C0), которая получается из общего решения y = j (x, C), если произвольному постоянному C придать определенное значение C=C0.
Итак, решить дифференциальное уравнение - значит:
1. Найти его общее решение или общий интеграл (если начальные условия не заданы).
2. Найти то частное решение, которое удовлетворяет заданным начальным условиям (если таковые имеются).
