Тема «Дифференциальное исчисление»
Вариант 1
1. Найти производные:
а). 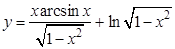 ; б).
; б). 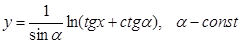 ;
;
в). 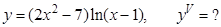 г).
г). 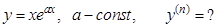
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 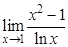 ; б).
; б). 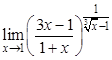 ; в).
; в). 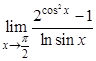
3. Провести полное исследование функций и построить их графики:
а). 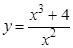 ; б).
; б). 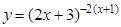 ;
;
4. Число 8 разбить на два таких слагаемых, чтобы сумма их кубов была наименьшей.
5. Найти углы, под которыми пересекаются данные линии: 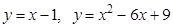 .
.
Вариант 2
1. Найти производные:
а). 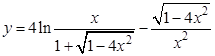 ; б).
; б). 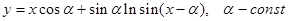 ;
;
в). 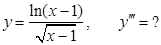 г).
г). 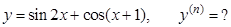
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 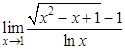 ; б).
; б).  ; в).
; в). 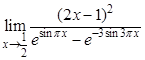
3. Провести полное исследование функций и построить их графики:
а). 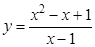 ; б).
; б). 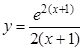 ;
;
4. Число 36 разбить на два таких слагаемых, чтобы сумма их квадратов была наименьшей.
5. Найти углы, под которыми пересекаются данные линии: 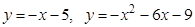 .
.
Вариант 3
1. Найти производные:
а). 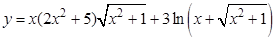 ; б).
; б). 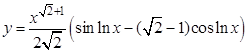 ;
;
в). 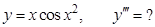 г).
г). 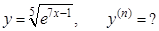
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 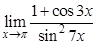 ; б).
; б). 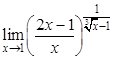 ; в).
; в). 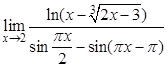
3. Провести полное исследование функций и построить их графики:
а). 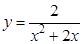 ; б).
; б). 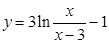 ;
;
4. Объем правильной треугольной призмы равен V. Какова должна быть стона основания, чтобы полная поверхность призмы была наименьшей?
5. Найти углы, под которыми пересекаются данные линии: 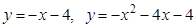 .
.
Вариант 4
1. Найти производные:
а). 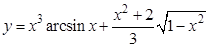 ; б).
; б). 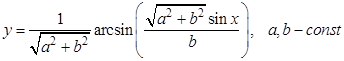 ;
;
в). 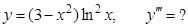 г).
г). 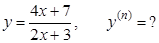
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 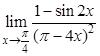 ; б).
; б). 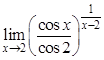 ; в).
; в). 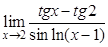
3. Провести полное исследование функций и построить их графики:
а). 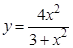 ; б).
; б). 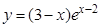 ;
;
4. Открытый бак имеет форму цилиндра. При данном объеме V, каковы должны быть радиус основания и высота цилиндра, чтобы его поверхность была наименьшей?
5. Найти углы, под которыми пересекаются данные линии: 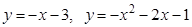 .
.
Вариант 5
1. Найти производные:
а). 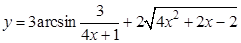 ; б).
; б). 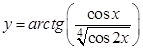 ;
;
в). 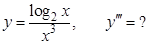 г).
г). 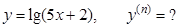
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 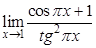 ; б).
; б). 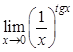 ; в).
; в). 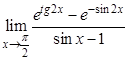
3. Провести полное исследование функций и построить их графики:
а). 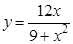 ; б).
; б). 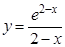 ;
;
4. Найти радиус и высоту цилиндра, имеющего объем V и наименьшую полную поверхность.
5. Найти углы, под которыми пересекаются данные линии: 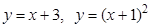 .
.
Вариант 6
1. Найти производные:
а). 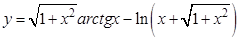 ; б).
; б). 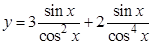 ;
;
в). 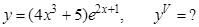 г).
г). 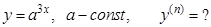
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 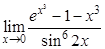 ; б).
; б). 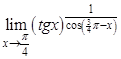 ; в).
; в). 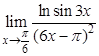
3. Провести полное исследование функций и построить их графики:
а). 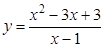 ; б).
; б). 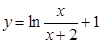 ;
;
4. Из круга вырезан сектор с центральным углом 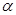 . Из сектора свернута коническая поверхность, при каком значении угла
. Из сектора свернута коническая поверхность, при каком значении угла 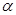 объем полученного конуса будет наибольшим?
объем полученного конуса будет наибольшим?
5. Найти углы, под которыми пересекаются данные линии: 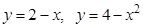 .
.
Вариант 7
1. Найти производные:
а). 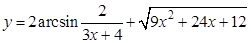 ; б).
; б). 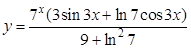 ;
;
в). 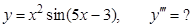 г).
г). 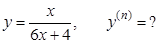
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 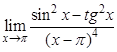 ; б).
; б). 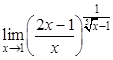 ; в).
; в). 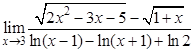
3. Провести полное исследование функций и построить их графики:
а). 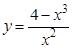 ; б).
; б). 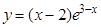 ;
;
4. Периметр равнобедренного треугольника равен 2р. Каковы должны быть его стороны, чтобы объем тела, образованно вращением этого треугольника вокруг его основания был наименьшим?
5. Найти углы, под которыми пересекаются данные линии: 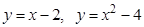 .
.
Вариант 8
1. Найти производные:
а). 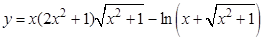 ; б).
; б). 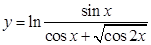 ;
;
в). 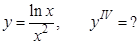 г).
г). 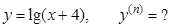
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 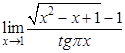 ; б).
; б). 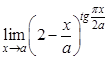 ; в).
; в). 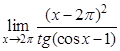
3. Провести полное исследование функций и построить их графики:
а). 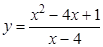 ; б).
; б). 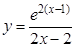 ;
;
4. При каких линейных размерах закрытая цилиндрическая банка данного объема V будет иметь наименьшую полную поверхность?
5. Найти углы, под которыми пересекаются данные линии: 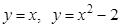 .
.
Вариант 9
1. Найти производные:
а). 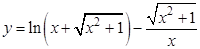 ; б).
; б). 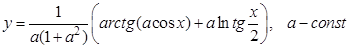 ;
;
в). 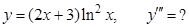 г).
г). 
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 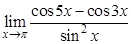 ; б).
; б). 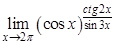 ; в).
; в). 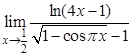
3. Провести полное исследование функций и построить их графики:
а). 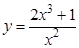 ; б).
; б). 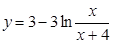 ;
;
4. Найти кратчайшее расстояние от точки М(2;2) до параболы 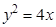 .
.
5. Найти углы, под которыми пересекаются данные линии: 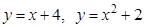 .
.
Вариант 10
1. Найти производные:
а). 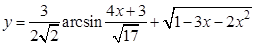 ; б).
; б). 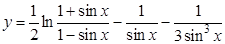 ;
;
в). 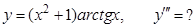 г).
г). 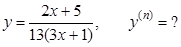
2. Пользуясь правилом Лопиталя, вычислить пределы функций:
а). 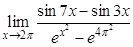 ; б).
; б). 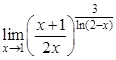 ; в).
; в). 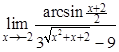
3. Провести полное исследование функций и построить их графики:
а). 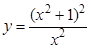 ; б).
; б). 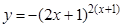 ;
;
4. На странице книги печатный текст должен занимать S кв.см. Верхнее и нижнее поля должны быть по a см., правое и левое – по b см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
5. Найти углы, под которыми пересекаются данные линии: 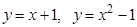 .
.
II семестр
