| 1. Найти предел: . | | | | 2.Составить уравнение касательной к кривой , перпендикулярно прямой, образующей с положительным направлением оси Ох угол 135°. Сделать чертеж. 3. Исследовать функцию и построить схематично ее график. | | 4. Вычислить определенный интеграл: | 5. Вычислить площадь фигуры, ограниченной линиями , , . Сделать чертеж. 6. Экспериментальные данные о переменных х и у приведены в таблице: В результате их выравнивания получена функция . Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. 7. Решить дифференциальное уравнение: . 8. Исследовать сходимость ряда: . | ВАРИАНТ 3 (для студентов, номера личных дел которых оканчиваются цифрой 3) Контрольная работа № 1 1.Дана матрица 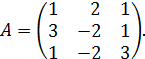 Найти ранг матрицы Найти ранг матрицы 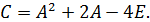 2. Методом обратной матрицы решить систему: 2. Методом обратной матрицы решить систему: 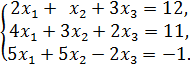 3. Определить, имеет ли однородная система 3. Определить, имеет ли однородная система 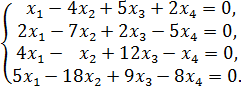 ненулевое решение. Найти общее решение системы. 4. Даны четыре вектора =(1;3;5); =(0;2;0); =(5;7;9); =(0;4;16) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе. 5. Найти собственные значения и собственные векторы линейного оператора , заданного матрицей А= . 6. Точки , и являются вершинами треугольника ABC. Составить уравнение высоты треугольника, опущенной из точки А на сторону ВС. Определить координаты точки Н – основания высоты АН треугольника АВС. Сделать чертеж. 7. Определить, находятся ли точки , , и на одной плоскости. Если это так, написать уравнение этой плоскости. Контрольная работа № 2 1.Найти предел: ненулевое решение. Найти общее решение системы. 4. Даны четыре вектора =(1;3;5); =(0;2;0); =(5;7;9); =(0;4;16) в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе. 5. Найти собственные значения и собственные векторы линейного оператора , заданного матрицей А= . 6. Точки , и являются вершинами треугольника ABC. Составить уравнение высоты треугольника, опущенной из точки А на сторону ВС. Определить координаты точки Н – основания высоты АН треугольника АВС. Сделать чертеж. 7. Определить, находятся ли точки , , и на одной плоскости. Если это так, написать уравнение этой плоскости. Контрольная работа № 2 1.Найти предел: | 2. Составить уравнения касательных к линиям и в точках их пересечения. Сделать чертеж. 3.Исследовать функцию и построить схематично ее график. | | 4. Вычислить определенный интеграл: | 5. Вычислить площадь фигуры, ограниченной линиями , , , . Сделать чертеж. 6.Экспериментальные данные о переменных х и у приведены в таблице: | | 0,5 | 1,0 | 1,5 | 2,5 | | | | 6,5 | 5,5 | 4,5 | 3,0 | 2,5 | В результате их выравнивания получена функция . Используя метод наименьших квадратов, аппроксимировать эти данные линейной зависимостью (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Сделать чертеж. 7.Решить дифференциальное уравнение: . 8. Исследовать сходимость ряда: . | |