Подбор параметров квадратичной функции методом наименьших квадратов
В эксперименте зарегистрированы значения 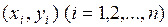 (рис. 5.3). Требуется методом наименьших квадратов подобрать параметры
(рис. 5.3). Требуется методом наименьших квадратов подобрать параметры 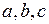 параболы
параболы 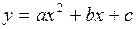 , соответствующей данной эксперимен-тальной зависимости. Имеем
, соответствующей данной эксперимен-тальной зависимости. Имеем
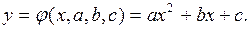
В этом случае выражение (5.2) имеет вид
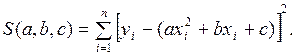 (5.8)
(5.8)
Это функция трех переменных 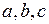 . Система уравнений (5.4) принимает вид
. Система уравнений (5.4) принимает вид
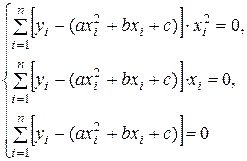
или в развернутом виде
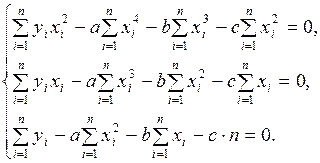 (5.9)
(5.9)
Получили систему линейных уравнений для определения неизвестных 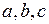 . Можно показать, что система имеет единственное решение, и что при полученных
. Можно показать, что система имеет единственное решение, и что при полученных 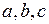 функция
функция 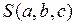 имеет минимум [3].
имеет минимум [3].
Задание на лабораторную работу
1. Из табл. 5.2 выбрать свой вариант задания.
2. Записать задание в виде табл. 5.1 (таблицы из 12 точек).
3. Построить на миллиметровой бумаге эти точки и, проанализировав характер их расположения на плоскости, выбрать вид функциональной зависимости.
4. Составить нормальную систему для коэффициентов 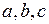 параболы
параболы 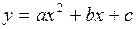 .
.
5. Решить полученную систему методом Гаусса. Записать вид функциональной зависимости. Найти невязку 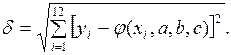
6. Построить полученную параболу на листе, на котором в пункте 3 нанесены экспериментальные точки.
7. Продолжить работу в компьютерном классе.
8. Получить с помощью компьютера аппроксимирующие многочлены третьего и четвертого порядков и выписать их невязки.
9. Выписать полученную на ЭВМ функциональную аппроксимацию эксперимента линейной комбинацией четырех функций 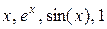 и ее невязку.
и ее невязку.
10. С помощью компьютера получить восемь законов функциональной зависимости и, проанализировав их невязки, сделать вывод о двух-трех лучших законах.
11. Оформить отчет по работе, в который входят: титульный лист; таблица значений эксперимента; таблица для определения коэффициентов нормальной системы уравнений аппроксимации квадратичной зависимостью; нормальная система уравнений; вид и невязка получившейся функциональной зависимости; график получившейся параболы с экспериментальными точками; полученные с помощью компьютера аппроксимирующие многочлены третьего и четвертого порядков; функциональная аппроксимация эксперимента линейной комбинацией четырех функций 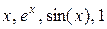 ; восемь законов функциональной аппроксимации линейной комбинацией трех функций и вывод о двух-трех лучших из них.
; восемь законов функциональной аппроксимации линейной комбинацией трех функций и вывод о двух-трех лучших из них.
Таблица 5.2
Варианты заданий
Значения 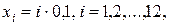 одинаковы для всех вариантов
одинаковы для всех вариантов
| № | 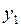 | 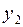 | 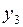 | 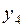 | 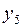 | 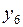 | 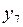 | 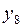 | 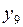 | 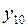 | 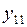 |  |
| 2,05 | 1,94 | 1,92 | 1,87 | 1,77 | 1,88 | 1,71 | 1,60 | 1,56 | 1,40 | 1,50 | 1,26 | |
| 2,09 | 2,05 | 2,19 | 2,18 | 2,17 | 2,27 | 2,58 | 2,73 | 2,82 | 3,04 | 3,03 | 3,45 | |
| 2,02 | 1,98 | 1,67 | 1,65 | 1,57 | 1,42 | 1,37 | 1,07 | 0,85 | 0,48 | 0,35 | -0,30 | |
| 1,99 | 2,03 | 2,20 | 2,39 | 2,19 | 2,61 | 2,35 | 2,60 | 2,55 | 2,49 | 2,50 | 2,52 | |
| 2,23 | 2,29 | 2,27 | 2,62 | 2,72 | 2,82 | 3,13 | 3,49 | 3,82 | 3,95 | 4,22 | 4,48 | |
| 2,07 | 2,17 | 2,21 | 2,31 | 2,10 | 2,09 | 2,12 | 1,63 | 1,78 | 1,52 | 1,16 | 1,07 | |
| 2,18 | 2,43 | 2,40 | 2,43 | 2,65 | 2,75 | 2,67 | 2,66 | 2,63 | 2,75 | 2,41 | 2,24 | |
| -0,10 | -0,21 | 0,01 | 0,05 | -0,13 | -0,23 | -0,21 | -0,43 | -0,57 | -0,44 | -0,44 | -0,83 | |
| -0,16 | 0,01 | 0,10 | 0,16 | 0,05 | 0,35 | 0,19 | 0,50 | 0,74 | 1,03 | 1,06 | 1,49 | |
| 2,09 | 2,31 | 2,72 | 2,77 | 2,78 | 2,97 | 3,00 | 3,51 | 3,43 | 3,58 | 3,58 | 3,54 | |
| 2,15 | 2,41 | 2,58 | 2,84 | 3,28 | 3,46 | 4,02 | 4,11 | 4,61 | 5,03 | 5,34 | 5,86 | |
| 0,10 | -0,01 | -0,19 | -0,11 | -0,31 | -0,78 | -0,64 | -0,85 | -1,18 | -1,39 | -1,79 | -2,02 | |
| 0,17 | 0,07 | 0,17 | 0,05 | 0,12 | 0,00 | 0,01 | -0,05 | -0,21 | -0,50 | -0,50 | -0,86 | |
| Окончание табл. 5.2 | ||||||||||||
| 0,80 | 0,29 | 0,52 | 0,77 | 0,93 | 1,20 | 1,20 | 1,35 | 1,39 | 1,48 | 1,52 | 1,71 | |
| 0,04 | 0,47 | 0,78 | 1,01 | 1,19 | 1,60 | 1,93 | 2,22 | 2,50 | 3,01 | 3,22 | 3,71 | |
| 0,08 | 0,14 | 0,37 | 0,36 | 0,44 | 0,48 | 0,27 | 0,39 | 0,50 | 0,48 | 0,69 | 0,50 | |
| -0,02 | 0,44 | 0,51 | 0,67 | 0,69 | 1,04 | 1,14 | 1,37 | 1,77 | 2,00 | 2,12 | 2,47 | |
| 0,14 | 0,23 | 0,44 | 0,54 | 0,72 | 0,76 | 0,37 | 0,64 | 0,57 | 0,44 | 0,41 | 0,30 | |
| -1,86 | -1,95 | -2,12 | -2,06 | -2,15 | -2,00 | -2,12 | -2,31 | -2,29 | -2,57 | -2,56 | -2,86 | |
| -1,65 | -2,00 | -1,87 | -1,89 | -1,75 | -1,59 | -1,44 | -1,51 | -1,51 | -1,17 | -0,87 | -0,47 | |
| 3,55 | 3,64 | 3,72 | 3,77 | 3,50 | 2,88 | 2,36 | 1,94 | 1,22 | 0,43 | 0,35 | -0,36 | |
| 0,35 | 0,41 | 0,85 | 0,99 | 1,34 | 1,35 | 1,79 | 2,32 | 2,78 | 2,94 | 3,45 | 4,01 | |
| 1,24 | 1,41 | 1,55 | 1,52 | 1,36 | 1,22 | 1,03 | 0,77 | 0,18 | 0,02 | -0,45 | -0,87 | |
| -0,33 | -0,25 | -0,04 | 0,12 | 0,34 | 0,41 | 0,28 | 0,45 | 0,08 | -0,32 | -0,77 | -1,35 | |
| 2,41 | 2,22 | 2,01 | 1,79 | 1,24 | 1,11 | 0,55 | 0,02 | -0,37 | -1,09 | -1,65 | -2,33 | |
| 2,41 | 2,46 | 2,52 | 2,64 | 2,78 | 2,77 | 2,83 | 2,99 | 3,17 | 3,39 | 3,65 | 4,33 | |
| 1,84 | 1,98 | 2,21 | 2,23 | 2,18 | 2,01 | 1,67 | 1,31 | 1,09 | 0,55 | -0,15 | -0,81 | |
| -0,31 | -0,98 | -1,11 | -1,02 | -0,18 | 0,33 | 0,79 | 1,34 | 1,84 | 2,47 | 3,11 | 3,81 | |
| 1,33 | 1,48 | 1,55 | 1,59 | 1,41 | 1,32 | 1,18 | 0,91 | 0,46 | 0,23 | -0,31 | -1,71 | |
| 0,15 | 0,23 | 0,39 | 0,51 | 0,67 | 0,87 | 0,92 | 1,24 | 1,56 | 1,91 | 2,32 | 2,57 |
