Интегрирование рациональных дробей
Многие задачи на вычисление интегралов с помощью подходящей подстановки сводятся к интегрированию рациональных дробей. 
Определение.Рациональной дробью называется выражение 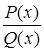 , где P(x) и Q(x) многочлены. Если степень многочлена Q(x) больше степени P(x), то рациональная дробь называется правильной. В противном случае – неправильной.
, где P(x) и Q(x) многочлены. Если степень многочлена Q(x) больше степени P(x), то рациональная дробь называется правильной. В противном случае – неправильной.
Приведем примеры правильных рациональных дробей:
I.  , II.
, II. 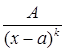 , III.
, III. 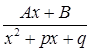 , IV.
, IV. 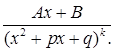
Здесь 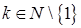 и
и  .
.
Определение. Рациональные дроби I  - IV называются простейшими.
- IV называются простейшими.
Заметим, что любую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной дроби.
Интеграл от многочлена сводится к первому табличному интегралу. Поэтому нужно научиться интегрировать правильные рациональные дроби. Из курса алгебры известно, что любую правильную рациональную дробь 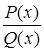 можно представить в виде суммы простейших дробей I – IV. Чтобы записать эту сумму, нужно пользоваться следующим правилом. Разложим знаменатель Q(x) на неприводимые многочлены
можно представить в виде суммы простейших дробей I – IV. Чтобы записать эту сумму, нужно пользоваться следующим правилом. Разложим знаменатель Q(x) на неприводимые многочлены 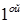 и
и 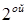 степени. Тогда каждому множителю из знаменателя вида (x – a) будет соответствовать простейшая дробь
степени. Тогда каждому множителю из знаменателя вида (x – a) будет соответствовать простейшая дробь 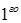 типа:
типа:  .Каждому множителю вида
.Каждому множителю вида 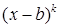 соответствует сумма дробей
соответствует сумма дробей 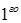 и
и 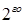 типа:
типа: 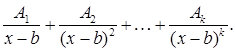
Множителю вида 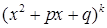 (где
(где 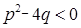 ) соответствует сумма простейших дробей
) соответствует сумма простейших дробей 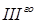 и
и 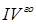 типов:
типов:
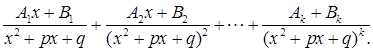
Неизвестные коэффициенты могут быть найдены из линейной системы, которая получится, если найденное нами равенство умножить на Q(x) и приравнять коэффициенты при одинаковых степенях x .Осталось теперь заметить, что интегралы от простейших дробей 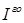 и
и 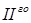 типов с помощью очевидной замены переменной сводятся к первому и второму табличным интегралам. А при интегрировании дроби третьего типа сначала в числителе выделяют производную знаменателя, умноженную на константу, так, чтобы оставшееся слагаемое не содержало x.Затем, числитель делится почленно на знаменатель, и полученные две дроби интегрируются отдельно. В той дроби, в которой числитель не зависит от x, нужно в знаменателе выделить полный квадрат и после очевидной замены получится тринадцатый табличный интеграл. Во втором интеграле нужно выделенную производную знаменателя внести под дифференциал и получить второй табличный интеграл.
типов с помощью очевидной замены переменной сводятся к первому и второму табличным интегралам. А при интегрировании дроби третьего типа сначала в числителе выделяют производную знаменателя, умноженную на константу, так, чтобы оставшееся слагаемое не содержало x.Затем, числитель делится почленно на знаменатель, и полученные две дроби интегрируются отдельно. В той дроби, в которой числитель не зависит от x, нужно в знаменателе выделить полный квадрат и после очевидной замены получится тринадцатый табличный интеграл. Во втором интеграле нужно выделенную производную знаменателя внести под дифференциал и получить второй табличный интеграл.
Пример 1. Вычислить 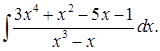
Заметим, что под знаком интеграла стоит неправильная дробь. Разделим числитель почленно на знаменатель с остатком:
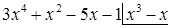
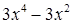
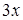
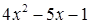
Отсюда следует: 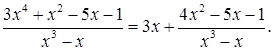
Разложим знаменатель на множители:
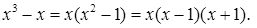
Разложим правильную дробь на простейшие:
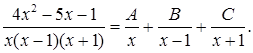
Умножим данное равенство на: 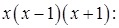
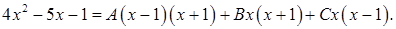 (1)
(1)
Независимые коэффициенты А, В, С можно найти, приравняв коэффициенты при  ,
, 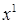 ,
, 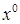 в равенстве (1). А можно это сделать быстрее.
в равенстве (1). А можно это сделать быстрее.
Равенство (1) справедливо при всех x.Подставим в (1) нули знаменателя подынтегральной функции: при x=0 из (1) следует -1=-A, А=1, при x=-1 из (1) следует 8=2C, С=4. Подставив в (1) x=1, получим –2=2В, В=-1. Таким образом,
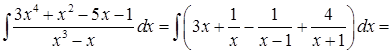
= 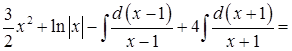
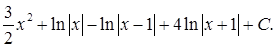
Пример 2. Вычислить 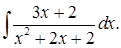
Подынтегральная функция здесь представляет простейшую дробь третьего типа. Вычислим интеграл «по плану, предложенному выше». Выделим в числителе производную знаменателя 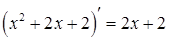 и вычислим интеграл:
и вычислим интеграл:
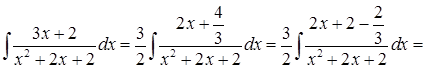
= 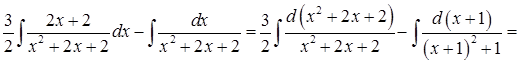
=