Линейные однородные дифференциальные уравнения с
постоянными коэффициентами.
Решение дифференциального уравнения вида 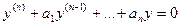 или, короче,
или, короче, 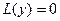 будем искать в виде
будем искать в виде 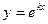 , где k = const.
, где k = const.
Т.к. 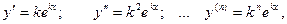 то
то
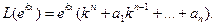
При этом многочлен 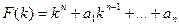 называется характеристическим многочленом дифференциального уравнения.
называется характеристическим многочленом дифференциального уравнения.
Для того, чтобы функция 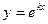 являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы
являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы
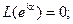 т.е.
т.е. 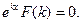
Т.к. ekx ¹ 0, то 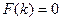 - это уравнение называется характеристическим уравнением.
- это уравнение называется характеристическим уравнением.
Как и любое алгебраическое уравнение степени n, характеристическое уравнение 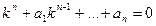 имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.
имеет n корней. Каждому корню характеристического уравнения ki соответствует решение дифференциального уравнения.
В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные.
Не будем подробно рассматривать каждый случай, а сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами.
1) Составляем характеристическое уравнение и находим его корни.
2) Находим частные решения дифференциального уравнения, причем:
a) каждому действительному корню соответствует решение ekx;
б) каждому действительному корню кратности m ставится в соответствие m решений:
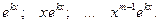
в) каждой паре комплексно – сопряженных корней 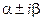 характеристического уравнение ставится в соответствие два решения:
характеристического уравнение ставится в соответствие два решения:
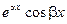 и
и 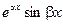 .
.
г) каждой паре m – кратных комплексно – сопряженных корней 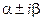 характеристического уравнения ставится в соответствие 2m решений:
характеристического уравнения ставится в соответствие 2m решений:
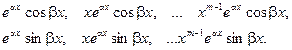
3) Составляем линейную комбинацию найденных решений.
Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами.
28.Линейные неоднородные дифференциальные уравнения. Теорема о структуре общего решения.
Структура общего решения.
Определение. Фундаментальной системой решенийлинейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения.
Определение. Если из функций yi с2耀тавить определитель n – го порядка
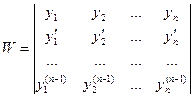 ,
,
то этот определитель называется определителем Вронского.
Теорема. Если функции 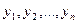 линейно зависимы, то составленный для них определитель Вронского равен нулю.
линейно зависимы, то составленный для них определитель Вронского равен нулю.
Теорема. Если функции 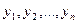 линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.
линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.
Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения 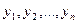 была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.
была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.
Теорема. Если 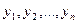 - фундаментальная система решений на интервале (a, b), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.
- фундаментальная система решений на интервале (a, b), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.
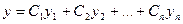 ,
,
где Ci –постоянные коэффициенты.
Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.
Линейные неоднородные дифференциальные уравнения.
Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.
Метод Бернулли.
Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций 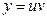 .
.
При этом очевидно, что 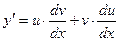 - дифференцирование по частям.
- дифференцирование по частям.
Подставляя в исходное уравнение, получаем:
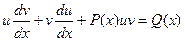
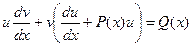
Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.
Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:
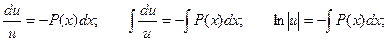
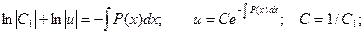
Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение 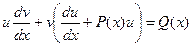 с учетом того, что выражение, стоящее в скобках, равно нулю.
с учетом того, что выражение, стоящее в скобках, равно нулю.
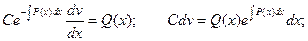
Интегрируя, можем найти функцию v:
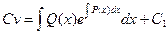 ;
; 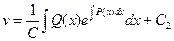 ;
;
Т.е. была получена вторая составляющая произведения 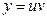 , которое и определяет искомую функцию.
, которое и определяет искомую функцию.
Подставляя полученные значения, получаем:
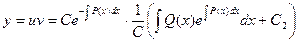
Окончательно получаем формулу:
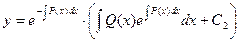 , С2 - произвольный коэффициент.
, С2 - произвольный коэффициент.
Это соотношение может считаться решением неоднородного линейного дифференциального уравнения в общем виде по способу Бернулли.
