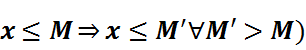Аксиоматика мн-ва действ.чисел. Важнейш.класс.действ.чисел

Отображегия. ф-ции. Важнейшие виды отобр. Элемент.ф-ции и их граф.

Пусть A, B - произвольные множества и f — закон (правило), по которому каждому элементу a ∈ A ставится в

соответствие единственный элемент b ∈ B. Тогда говорят, что задано отображение f множества A в множество B или

оператор f, переводящий множество A в множество B. Отображение f множества A в B обозначают f : A → B или

Пусть A, B - произвольные множества и f — закон (правило), по которому каждому элементу a ∈ A ставится в

соответствие единственный элемент b ∈ B. Тогда говорят, что задано отображение f множества A в множество B или

оператор f, переводящий множество A в множество B. Отображение f множества A в B обозначают f : A → B или

Пусть A, B - произвольные множества и f — закон (правило), по которому каждому элементу a ∈ A ставится в

соответствие единственный элемент b ∈ B. Тогда говорят, что задано отображение f множества A в множество B или

оператор f, переводящий множество A в множество B. Отображение f множества A в B обозначают f : A → B или

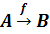(читается: «f отображает A в B»).

Элемент b ∈ B, в который отображен a ∈ A, называют образом элемента a при отображении f и обозначают f(a).

Элемент a в этом случае называют прообразом элемента f(a).

Определение отображения коротко записывают в виде:

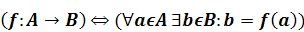
Определение 1. Отображение f : A → B называют взаимно однозначным или биективным, если каждый элемент

b ∈ B является образом только одного элемента a ∈ A.

Если отображение f : A → B есть взаимно однозначное соответствие между элементами множеств A и B, то можно

говорить об обратном отображении.

Определение2. Отображение 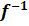называют обратным к отображению f,если 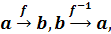т.е. элементу b ∈ B

ставится в соответствие тот элемент a ∈ A, образом которого при отображении f является b:

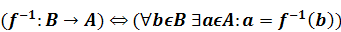
Определение 3. Два множества A и B называются эквивалентными (равномощными), если существует хотя бы одно взаимно однозначное отображение одного множества на другое, и обозначаются A ∼ B.

Всякое множество, эквивалентное множеству натуральных чисел, называется счетным. (читается: «f отображает A в B»).

Аксиоматика мн-ва действ.чисел. Важнейш.класс.действ.чисел.

Определение 1. Множество R называется множеством действительных чисел, а его элементы действительными числами, если выполняется следующая система аксиом:

I. Аксиомы сложения.

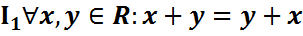(коммутативный закон)

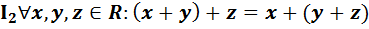(ассоциативный закон).

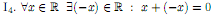
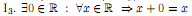(существование в R нуля). (существование в R противоположного элемента).

II. Аксиомы умножения.

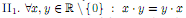(коммутативный закон).

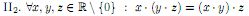(ассоциативный закон).

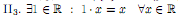(существование нейтрального элемента).

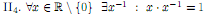(существование обратного элемента).

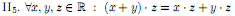(дистрибутивный закон относительно сложения).

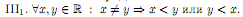III. Аксиомы порядка.

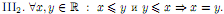
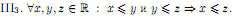
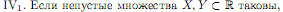
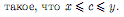
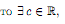
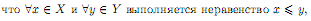
Определение 1. Множество X ⊂ R называется ограниченным сверху (снизу), если существует c ∈ R, что x≤c(c≤x)

для ∀x ∈ X.

Определение 2. Множество называется ограниченным, если оно ограничено сверху и снизу. Определение 2 означает, что множество X ограничено в том и только том случае, если оно расположено на некотором конечном промежутке числовой прямой. Определение 3. Элемент a ∈ X называется наибольшим (наименьшим) элементом для множества X, если x≤a

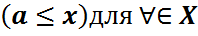для ∀x ∈ X и обозначается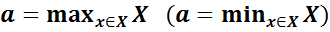

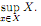Определение 4. Наименьшее из чисел, ограничивающих множество X ⊂ R сверху, называется верхней гранью множества X (точной верхней гранью) и обозначается

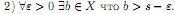Таким образом, если s = supX, то: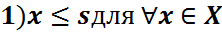

Определение 5. Наибольшее из чисел, ограничивающих множество X ⊂ R снизу, называется нижней гранью множества X и обозначается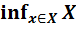

Таким образом, если L = inf X, то: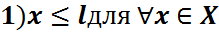

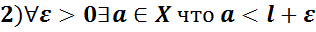
Любое ограниченное сверху множество X ∈ R имеет бесконечно много верхних граней. В самом деле, если действительное число M является одной из верхних граней множества X, то любое действительное число M^’> M также является верхней гранью множества X (так как