Теоремы сложения и умножения вероятностей. Условная вероятность. Независимость событий
Случайные события. Операции над событиями.
События, происходящие вокруг нас, можно разделить на 3 вида: достоверные, невозможные и случайные.
Достоверным называется событие, которое неизменно происходит при выполнении некоторого комплекса внешних условий.
Невозможным называется событие, которое заведомо не происходит при выполнении некоторого комплекса внешних условий.
Случайным называется событие, которое может либо происходить либо не происходить при выполнении некоторого комплекса внешних условий.
Суммой событий A и B называется событие A+B такое, что наступит событие А, либо наступит событие B , либо оба вместе.
Произведением событий А и B называется событие AB такое, которое происходит при одновременном наступлении событий А и B.
Событием, противоположным событию B) называется такое событие, при котором не происходит событие B.
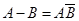 Разностью событий А и B называется такое событие, которое состоится, если событие А произойдет, а событие B не произойдет.
Разностью событий А и B называется такое событие, которое состоится, если событие А произойдет, а событие B не произойдет.
Два события называются совместными, если наступление одного из них не исключает наступление другого в том же испытании. Два события называются несовместными, если их совместное наступление невозможно.
Определения вероятности: классическое, статистическое, аксиоматическое. Геометрическая вероятность.
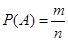 |
(классическое). Вероятностью Р(А) события А называют отношение где n – общее число всех возможных элементарных исходов испытания; m – число возможных элементарных исходов, благоприятствующих событию А.
Элементарными событиями, благоприятствующими событию А, называют элементарные события, входящие в состав события А.
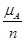
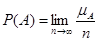
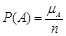 (статистическое). За вероятность Р(А) события А принимают отношение числа испытаний, в которых наступило событие А, к общему числу произведенных испытаний или
(статистическое). За вероятность Р(А) события А принимают отношение числа испытаний, в которых наступило событие А, к общему числу произведенных испытаний или
Величину называют относительной частотой события А.
Утверждение. Относительные частоты обладают свойством устойчивости.
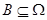
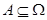
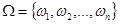 (аксиоматическое). Пусть - множество элементарных событий. ,
(аксиоматическое). Пусть - множество элементарных событий. ,
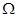 Определим на множестве неотрицательную меру, называемую вероятностью, со свойствами:
Определим на множестве неотрицательную меру, называемую вероятностью, со свойствами:
1) 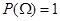 (вероятность достоверного события равна единице);
(вероятность достоверного события равна единице);
2) 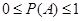
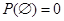 (вероятность невозможного события равна нулю);
(вероятность невозможного события равна нулю);
3) для любого события А;
4) 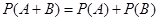 если А и B – несовместные события
если А и B – несовместные события
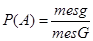 Определение 4 (геометрическое). Вероятность попадания в область g при бросании точки наудачу в область G равна
Определение 4 (геометрическое). Вероятность попадания в область g при бросании точки наудачу в область G равна
где mes – мера области ( длина, площадь, объем).
Теоремы сложения и умножения вероятностей. Условная вероятность. Независимость событий.
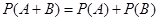 Теорема 1.Еслисобытия А и B несовместны, то вероятность суммы этих событий равна сумме их вероятностей.
Теорема 1.Еслисобытия А и B несовместны, то вероятность суммы этих событий равна сумме их вероятностей.
Теорема 2. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного наступления.
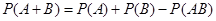
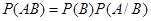
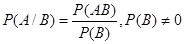 Условной вероятностью события А называют вероятность события А, вычисленную в предположении, что некоторое событие B уже наступило.
Условной вероятностью события А называют вероятность события А, вычисленную в предположении, что некоторое событие B уже наступило.
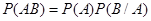 |
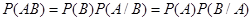 Вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
Вероятность совместного наступления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
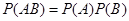
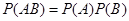 Теорема 3. Вероятность совместного наступления двух независимых событий равна произведению их вероятностей.
Теорема 3. Вероятность совместного наступления двух независимых событий равна произведению их вероятностей.
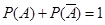 События А и B называются независимыми, если выполняется условие
События А и B называются независимыми, если выполняется условие
Сумма вероятностей противоположных событий равна единице.
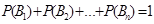 Сумма вероятностей событий, образующих полную систему, равна единице.
Сумма вероятностей событий, образующих полную систему, равна единице.
5. 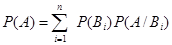 Формула полной вероятности. Формула Байеса.
Формула полной вероятности. Формула Байеса.
- формула полной вероятности.
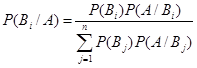 | 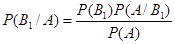 | ||
- формула Байеса в общем виде.
