Найдите наименьшее натуральное число, квадрат которого оканчивается на 2009

Ответ: 1747. Решение: Пусть наше число равно N, тогда число (N²–9) оканчивается на 2000. Значит, (N²–9)=(N–3)(N+3) делится на 2000=2⁴×5³. Делиться на 5 может только один из двух множителей (N–3) и (N+3), т.к. их разность 6 не делится на 5. При этом оба множителя должны быть чётными, но одновременно не делящимися на 4, значит, один из них делится на 2, другой – на 2³=8. Таким образом, один из этих множителей делится на 2×5³=250, а ещё один – на 8, причём это может быть один и тот же множитель. Разобрав случаи для (N–3) и (N+3) чисел 250, 500, 750, 1000, 1250, 1500, 1750, обнаружим, что условия делимости выполняются для N равных 253, 747, 997, 1003, 1253, 1747. Первым из квадратов, оканчивающихся на 2009, будет 1747²=3052009.

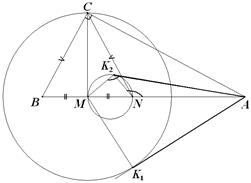4. На гипотенузе АВ прямоугольного треугольника АВС нашлись такие точки M и N, что BM=MN и BC=CN. Из точки А к окружности w₁ (c центром М и радиусом МС) и к окружности w₂ (с диаметром MN) проведены касательные AK₁ и AK₂ соответственно (K₁ и K₂ – точки касания). Докажите, что AK₁=AK₂.

Решение: Т.к. АК₂ – касательная, то из свойств вписанных углов следует, что треугольники AMK₂ и ANK₂ подобны. Тогда AK₂²=AM×AN=AM×(AM–MN)=AM²–AM×MN=AM²–AM×BM=AM²–СM²=AM²–MK₁²=AK₁², откуда и следует нужное нам равенство AK₁=AK₂. (Мы воспользовались равенством AM×BM=СM², т.к. СМ – высота из вершины прямого угла.)

5. На полях a1, a2 и b1 шахматной доски стоят соответственно белая, чёрная и красная ладьи. Разрешается делать ходы по обычным правилам, однако после любого хода каждая ладья должна быть под защитой какой-нибудь другой ладьи (т.е. в одной горизонтали или вертикали с другой ладьёй). Сколько ещё других (не считая исходной) расстановок этих ладей на шахматной доске можно получить?

Ответ: 9407 расстановок. Решение: Заметим, что эти три ладьи всегда располагаются в трёх клетках, лежащих в углах некоторого прямоугольника со сторонами, параллельными сторонам доски («квартета» из четырёх клеток, находящихся на пересечении двух горизонталей и двух вертикалей). При этом их порядок по часовой стрелке совпадает с исходным, т.е. белая, чёрная и красная ладьи. Нетрудно убедиться, что возможно любое из таких расположений. Для этого ладьи сначала сдвигаются в три угла такого квартета (передвигаются в две вертикали, потом в две горизонтали квартета, сохраняя друг друга под защитой), а затем перемещаются по очереди по часовой стрелке через свободный угол. Всего существует 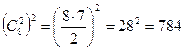таких квартетов, что определяется выбором двух горизонталей и двух вертикалей, на пересечении которых и будут находиться четыре угла соответствующего прямоугольника. В каждом таком прямоугольнике существуют 4×3=12 расстановок ладей по часовой стрелке, т.к. ладьи всегда образуют уголок, в центральной клетке которого может находиться любая ладья (3 варианта), а сама центральная клетка может находиться в любом из углов квартета (4 варианта). Учитывая исходный вариант, получим всего 784×12–1=9407 расстановок.

11 класс

1. Докажите, что существует бесконечно много арифметических прогрессий 1, b, c, таких, что квадратный трехчлен x²+bx+c имеет действительные корни.

Решение: Заметим, что из свойств арифметической прогрессии следует, что 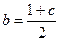. Кроме того, для наличия действительных корней дискриминант данного квадратного трехчлена 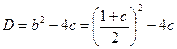должен быть неотрицательным. Получившееся неравенство равносильно квадратному неравенству c²–14c+1³0, имеющему бесконечно много решений, значит, существует и бесконечно много арифметических прогрессий, удовлетворяющих условию.

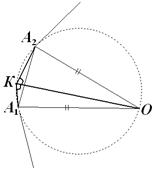2. В плоскости правильного n-угольника А₁А₂…А_n отмечена точка К так, что биссектриса угла А₁КА₂ проходит через центр этого n-угольника. Покажите, что точка К необязательно лежит на серединном перпендикуляре к отрезку А₁А₂.

Решение: Точка К может лежать на дуге А₁А₂ описанной около треугольника А₁А₂O окружности (где О – центр n-угольника), не совпадая с серединой этой дуги. В этом случае КО будет биссектрисой ÐА₁КА₂, что верно в силу свойств вписанных углов, т.к. А₁О=А₂О. Точка К в этом случае не лежит на серединном перпендикуляре к отрезку А₁А₂.

3. В клетках таблицы 3´3 расставлены положительные числа так, что каждое число в два раза меньше суммы всех чисел, находящихся в соседних с ним по стороне клетках. Верно ли, что среди этих 9 чисел можно выделить две группы по 4 числа с одинаковыми суммами?

Решение: Заметим, что каждое угловое число равно полусумме своих соседей, тогда сумма всех угловых чисел равна удвоенной полусумме чисел, находящихся в серединах сторон, т.к. каждое такое число учитывается дважды, являясь соседом у двух угловых чисел. Значит, сумма четырёх угловых чисел равна сумме четырёх чисел в серединах сторон. Таким образом, требуемое условие выполнимо.

Комментарий: Но … условие задачи некорректно, т.к. такое расположение чисел возможно только в случае, если все числа равны 0, что нетрудно доказать, решив соответствующую систему из 9 уравнений с 9 неизвестными. Поэтому верным является вывод о некорректности условия задачи.

Примечание: доказательство «верности» требуемого в задаче оценивается из 7 баллов, доказательство некорректности условия оценивается из 10 баллов.

4. Все углы при вершине S треугольной пирамиды SАВС равны 60°. Докажите, что полупериметр основания АВС больше наибольшего из рёбер SA, SB и SC.

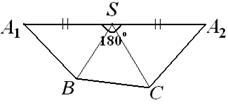Решение: Сделаем развёртку A₁BCA₂S, разрезав пирамиду по наибольшему из данных трёх рёбер (с точностью до обозначений можно считать, что это ребро SA) – см. рис. Т.к. сумма углов при вершине S равна 180°, то S лежит на отрезке A₁A₂. Тогда длина ломаной A₁BCA₂ больше A₁A₂, т.е. периметр основания АВС пирамиды больше удвоенного ребра SA, откуда и следует нужное нам утверждение.

На олимпиаде школьники решали 6 задач. Оказалось, что никакие два из них не решили вместе всех задач, и каждую задачу решило ровно 100 школьников. При каком наименьшем числе школьников это возможно?

Ответ: 200 школьников, например, 4 группы по 50 человек, каждый решил по 3 задачи – группа А решила 1, 2 и 3 задачи; В – 1, 4 и 5; С – 2, 4 и 6; D – 3, 5 и 6. Доказательство оценки: Если школьников менее 200 (а всего предъявлено 600 решений), то по принципу Дирихле найдётся школьник N, решивший хотя бы 4 задачи (но, согласно условию, не все 6). Если N решил 5 задач, то вместе с любым школьником, решившим оставшуюся задачу, он составит «запретную» пару, противоречащую условию. Если он решил 4 задачи, то по оставшимся двум задачамсреди 200 решений, предъявленных не более чем 198 школьниками, найдутся два решения, принадлежащих одному и тому же школьнику, который вместе с N составит «запретную» пару. Противоречие, значит, всего в олимпиаде участвовало не менее 200 школьников.

6. Существует ли натуральное число, которое, будучи записанным дважды подряд (в десятичной записи), даст точный квадрат?

Ответ: существует, например, число 183673469387755102041, т.к. 183673469387755102041183673469387755102041=428571428571428571429²= .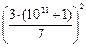

Решение: Пусть наше число а имеет n цифр, тогда будучи записанным дважды оно даст число А=а×(10ⁿ+1). Найдём такое натуральное n, что 10ⁿ+1 делится на какой-нибудь точный квадрат, например, 7²=49. Подойдёт n=21, т.к. 10²¹º100¹⁰×10º2¹⁰×10º10240º –1(mod 49). Но после деления на 49 останется число из 20 цифр, начинающееся на 2, поэтому домножим наше число на точный квадрат 3²=9. Тогда получим нужное нам 21-значное число .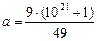

Комментарий: в качестве примера также подойдёт число 8264462810082644628100=90909090910²= 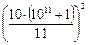, т.к. (10¹¹+1) делится на 11², тогда нужное нам 11-значное число 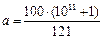. Другие примеры можно получить по аналогичной схеме.