Критерий, основанный на известных вероятностных состояниях «природы»

Если известны вероятности состояний «природы» (например, спроса по данным анализа за прошлые годы):

Р₁ = Р(П₁); Р₂ = Р(П₂); … ; Р_n = Р(П_n),

полагая, что Р₁ + Р₂ + …+ Р_j +…+ P_n = 1.

Тогда в качестве показателя эффективности (рациональности, обоснованности) стратегии T_i берется среднее (математическое ожидание) – выигрыш применения этой стратегии:

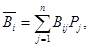
а оптимальной считают стратегию, для которой этот показатель эффективности имеет максимальное значение, то есть

.

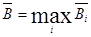Если каждому решению T_i соответствует множество возможных результатов 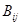с вероятностями 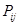, то среднее значение выигрыша определится

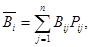а оптимальная стратегия выбирается по условию .

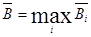В этом случае можно воспользоваться и стратегией минимального среднего риска для каждого i-го состояния «природы»:

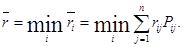
2. Максиминный критерий Вальда.Здесь выбирается решение, например, торговой организации, при котором гарантируется максимальный выигрыш в наихудших условиях внешней среды (состояния «природы»):

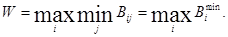
3. Критерий пессимизма-оптимизма Гурвица.Здесь представляется логичным, чтобы при выборе решения вместо двух крайностей в оценке ситуации (оптимизм – пессимизм) придерживаться некоторого компромисса, учитывающего возможность как наихудшего, так и наилучшего поведения «природы». В соответствии с этим компромиссным критерием для каждого решения будет линейная комбинация минимального и максимального выигрышей и выбирается тот, для которого эта величина окажется наибольшей:

,

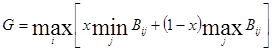где х – показатель пессимизма – оптимизма (чаще всего 0,5).

4. Критерий минимаксного риска Сэвиджа.Здесь выбирают ту стратегию, при которой величина риска имеет минимальное значение в самой неблагоприятной ситуации:

,

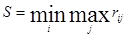чтобы избежать слишком большого риска при выборе решения.

Комплексный анализ всех этих критериев позволяет в какой-то мере оценить возможные последствия принимаемых решений.

Пример. Известна матрица условных вероятностей Р_ij продажи старых товаров С₁, С₂, С₃ при наличии новых товаров Н₁, Н₂, Н₃ (см. табл.4).

Таблица 4

Старые товары	Новые товары
Н1	Н2	Н3
С1	0,6	0,3	0,6
С2	0,2	0,7	0,2
С3	0,1	0,4	0,5

Определить наиболее выигрышную политику продаж.

Решение. Минимальный выигрыш: .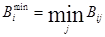

Минимальный выигрыш при продаже старого товара:

С₁: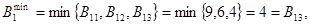

С₂: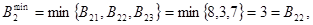

С₃: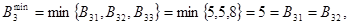

где В₁₂, В₂₂, В₃₁, В₃₂ образуют систему пессимистических оценок выигрыша от продаж старых товаров.

Максимальный выигрыш: .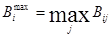

Максимальный выигрыш при продаже старых товаров:

С₁: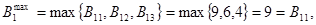

С₂: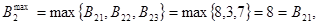

С₃: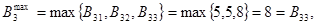

где В₁₁, В₂₁, В₃₃ образуют систему оптимистических оценок выигрыша от продаж старых товаров.

При анализе «игры с природой» вводится показатель влияния какого-либо состояния «природы» на исход продаж, то есть показатель риска:

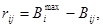
каждый из которых составит матрицу рисков (см.табл.5).

Таблица 5

Товары	Н1	Н2	Н3
С1
С2
С3

Максимальное значение риска для каждого решения:

,

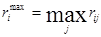то есть при продаже товаров:

С₁: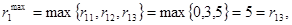

С₂: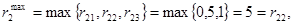

С₃: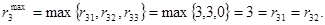

Решение о плане продаж принимается, исходя из анализа системы критериев.

Критерий по известным вероятностным состояниям «природы» P_ij: оптимальным считают стратегию, для которой этот показатель наибольший, то есть:

,

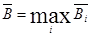где 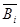- математическое ожидание выигрыша при i-й стратегии:

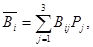
где B_ij – результат (выигрыш при применении ij-й стратегии):

=

=

=

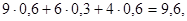
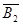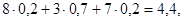
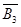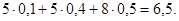
Тогда 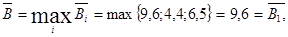то есть оптимальной стратегией по этому критерию будет продажа изделия С₁.

Максиминный критерий Вальда:

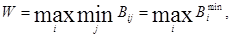
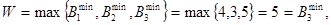
то есть при продаже изделия С₃ гарантируется выигрыш даже в наихудших условиях.

Критерий пессимизма – оптимизма Гурвица:

,

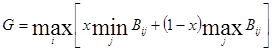где х – доля оптимизма – пессимизма (0,5).

,

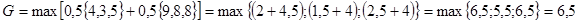то есть, исходя из уравновешенной точки зрения, принимается решение о продажах С₁, С₃.

Критерий минимаксного риска Сэвиджа, по которому принимают решение минимальным значением риска в самой неблагоприятной ситуации:

,

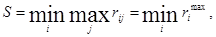где 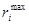вычислена по матрице рисков.

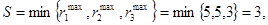
что соответствует целесообразности в смысле этого критерия продажам изделия С₃.

Комплексный анализ всех критериев позволяет предположить, что наилучшей стратегией продаж будет продажа изделий Н₁, Н₂, Н₃, С₁, С₃. Изделие С₂ должно быть снято с продаж.

Теория очередей.

Многие экономические задачи связаны с системами массового обслуживания, в которых происходит удовлетворение требований на выполнение каких-либо услуг.

Исследованием систем массового обслуживания (СМО) занимается теория очередей, на начальное развитие которой оказали особое влияние труды датского ученого А.К. Эрланга (1878-1929) в области проектирования и эксплуатации телефонных станций. Общая схема СМО показана на рис.1.

Входной Правило Правило Каналы Выходной

поток постановки Очередь обслуживания обслуживания поток

требований в очередь требований

Рисунок 1.

Требование на обслуживание (например, неисправный автомобиль, судно) поступает в обслуживающую систему (автомастерскую, порт). Если есть свободные каналы обслуживания (мастера, причалы), то требование выполняется. Если все каналы заняты, то требование ставится в очередь по определенным правилам или покидает систему не обслуженным.

Основная задача теории массового обслуживаниясводится к определению оптимального соотношения между входным потоком требований и числом обслуживающих каналов, при котором общие суммарные затраты минимальны.

Общие суммарные затраты складываются из затрат обслуживания и затрат ожидания, причем по мере увеличения сервиса затраты обслуживания увеличиваются, а затраты ожидания уменьшаются.

СМО можно описать, задавая следующие ее компоненты:

· входной поток требований,

· дисциплину очереди,

· механизм обслуживания.

Входной поток требований характеризуется вероятностным законом распределения моментов поступления требований в систему и количеством требований в каждом поступлении.

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких задач теории очередей, в которых поток требований является простейшим (пуассоновским).

Простейший поток событий обладает тремя свойствами:

1. стационарностью – постоянным количеством событий в единицу времени;

2. отсутствием последействия – независимостью количества событий после любого момента времени от количества событий до него;

3. ординарностью – практической невозможностью одновременного поступления нескольких требований.

Для простейшего потока частота наступления событий подчиняется закону Пуассона, то есть вероятность того, что за время t произойдет k событий, определяется:

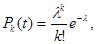
где 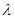- количество событий в единицу времени (интенсивность потока).

Вероятность того, что один причал занят (k=1) при отказе в среднем в единицу времени двух причалов ( 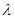=2):

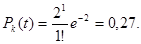
Вероятность того, что все причалы свободны – 13%; вероятность того, что один причал занят – 27%; два – 27%; три – 18%; четыре – 9% и т.д.

По теореме сложения вероятностей, вероятность суммы независимых событий равна сумме вероятностей этих событий, отсюда вероятность отказа в единицу времени не более четырех причалов равна сумме вероятностей отсутствия отказа и вероятностей отказа одной, двух, трех, четырех причалов:

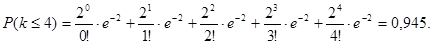
Вероятность отказа более четырех причалов:

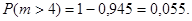
Дисциплина очереди описывает порядок обслуживания требований в системе. Длина очереди может быть ограниченной или неограниченной. Правила постановки в очередь: FIFO– «первым пришел первым обслуживаешься», LIFO– «последним пришел первым обслуживаешься», по другим приоритетам или случайно.

Механизм обслуживания характеризуется продолжительностью процедур обслуживания и количеством одновременно обслуживаемых требований.

Время обслуживания требований в системе является случайной величиной и обычно описывается экспоненциальным законом распределения, то есть распределение длительности оставшейся части работ по обслуживанию не зависит от того, сколько оно уже продолжалось.

Вероятность того, что время обслуживания не превосходит некоторой величины t, определяется формулой:

,

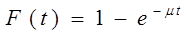где 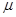- величина, обратная среднему времени обслуживания.

Введем в рассмотрение параметр 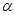- коэффициент загрузки системы или среднее число каналов (причалов), которые необходимо иметь, чтобы обслуживать в единицу времени все поступающие требования (суда):

,

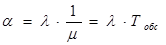где 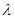- среднее число требований, поступающих в единицу времени;

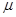- среднее число требований, удовлетворяемых в единицу времени;

Т_обс – среднее время обслуживания одним каналом одного требования.

Заметим, что, если 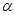меньше количества каналов обслуживания, то очередь не может расти безгранично, то есть число обслуживающих каналов должно быть больше среднего числа каналов, необходимых для того, чтобы за единицу времени обслужить все поступившие требования.

Различают следующие виды СМО. В зависимости от условий ожидания требованием начала обслуживания различают СМО с отказами и с ожиданием.

В системах с отказами требования, поступающие в момент, когда все каналы обслуживания заняты, получают отказ и утрачиваются.

В системах с ожиданием требование, застав все обслуживающие каналы занятыми, ставится на очередь вплоть до освобождения любого из каналов.

СМО, допускающие очередь, но с ограниченным числом требований в ней, называются системами с ожиданием и ограниченной длиной очереди.

СМО, допускающие очередь, но с ограниченным сроком пребывания каждого требования в ней, называются системами с ограниченным временем ожидания.

СМО, допускающие очередь, но с ограниченным числом циркулирующих в системе требований, называются системами с ограниченным потоком требований.

По числу каналов обслуживания различают одноканальные и многоканальные системы.

По числу фаз обслуживания – однофазные и многофазные (последовательная обработка требований на нескольких каналах).

Вместо заключения:

В жизни почти всегда бывает так, что человек, владеющий разными инструментами (по своей профессии) и применяющий их в зависимости от характера выполняемой работы, добивается лучших результатов, чем человек, владеющий лишь универсальным приемом.

В одних случаях можно выполнить вычисления устно, в других – необходим лист бумаги для расчетов, в-третьих – расчет на компьютере, в-четвертых – привлечение специальной программы оптимизационных расчетов.

Нужно знать и уметь пользоваться универсальными и частными приемами, которые ведут к цели быстрее и легче.

Афоризмы классиков математического моделирования:

Математика имеет хороший инструмент. Экономика обладает хорошим материалом. Экономико-математические методы – это совмещение хорошего инструмента с хорошим исходным материалом.

Генрих Герц

В мире не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума.

Леонард Эйлер

Любая модель принесет мало пользы при отсутствии необходимой информации.

Х. Таха

Исследование операций как средство решения задач организационного управления можно рассматривать и как науку, и как искусство.

Х. Таха

Математика подобна мясорубке, она может переработать любое мясо, но для того, чтобы получить хорошие котлеты, нужно и хорошее мясо.

Томас Генри Гексли

Самый большой и наименее рациональный риск из всех возможных – риск ничегонеделания.

П.Ф. Драккер

Гений мыслит и создает. Человек обыкновенный приводит в исполнение. Дурак пользуется и не благодарит.

К. Прутков

Нужно иметь храбрость, поверить в свои убеждения, иначе самое интересное, что могло прийти вам в голову, заберут другие.

Норберт Винер

[1] Канторович Леонид Витальевич (1912-1986) – математик и экономист. Основные труды по функциональному анализу, вычислительной математике. Положил начало линейному программированию. Один из создателей в СССР теории оптимального планирования и управления нар. хозяйством, теории оптимального использования сырьевых ресурсов. В 1975 совместно с американским ученым Т. Купмансом получил Нобелевскую премию за вклад в теорию оптимизации ресурсов.

[2] Анализ – разложение, расчленение целого на составные элементы с целью установления взаимосвязи и взаимозависимости между ними. Для обобщения результатов анализа необходимо осуществить синтез, то есть объединить части в целое.

[3] Антагонизм(от греч. antagonisma – спор, борьба) – противоречие, характеризующееся острой борьбой враждебных сил, тенденций.