Решение задачи Коши методом Нюстрема

Так как система имеет третий порядок, записываем три уравнения функции правых частей:

Задаем нулевые начальные условия:

Находим решение СДУ :

Процессы, полученные данным численным решением выглядят следующим образом:

Рисунок 26 – Зависимость i(t) при пуске ЭМС, найденная методом Эйлера.

Рисунок 27 – Зависимость 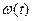при пуске ЭМС, найденная методом Эйлера.

Рисунок 28 – Зависимость U(t) при пуске ЭМС, найденная методом Эйлера.

Моделирование двухконтурной ЭМС в программной среде MATLAB Simulink c ограничением тока якоря ДПТ НВ

Введем в систему внутренний контур регулирования тока якоря ДПТ НВ, настроенный на выходной ток, равный двухкратному номинальному току двигателя при максимальном значении напряжения управления U_зад=10 В. В этом случае коэффициент обратной связи по току:

При полученном коэффициенте обратной связи настроим ПИ-регулятор тока так, чтобы обеспечивалось указанное в задании перерегулирование (не более 5%), а также подадим на ЭМС номинальную нагрузку ( ) при пуске. Коэффициенты ПИ-регулятора принимаем равным K_рт=1; Т_рт=0,001 с. Ограничиваем выходное напряжение П-регулятора скорости на уровне ±10 В для ограничения тока якоря на уровне двукратного номинального.

Рисунок 29 – Имитационная модель нелинейной двухконтурной ЭМС при пуске под нагрузкой

Рисунок 30 – Переходные процессы в нелинейной ЭМС при пуске под номинальной нагрузкой

Заключение

В данной работе была исследована математическая модель системы регулирования скорости двигателя постоянного тока. Были рассчитаны переходные процессы изменения тока якоря и скорости двигателя, а также напряжения управления при пуске ЭМС вхолостую тремя различными аналитическими методами и одним численным.

Для подтверждения правильности решения системы уравнений, описывающих ЭМС, проводилось моделирование линейной системы управления электроприводом в программной среде MATLAB. Графики переходных процессов при имитационном моделировании совпали с решением СДУ различными методами.

К использованным аналитическим методам относятся аналитический, операторный и метод определителей Вандермонда. Решения всех трех методов сошлись друг с другом, что доказывает правильность их использования. Наиболее громоздким из аналитических оказался классический метод, а более простым и быстрым – метод преобразования Лапласа.

Аналогичное решение СДУ дал численный метод Рунге-Кутта пятого порядка. Данный численный метод является довольно громоздким, а также требует большой вычислительной мощности персонального компьютера.

Методом секущих с точностью Δ=0,00001 были определены все показатели качества переходного процесса скорости двигателя при пуске вхолостую.

Также было проведено имитационное моделирование нелинейной ЭМС с ограничением тока якоря.