Геометрическая задача для толстостенной трубы
Расчёт балки конечной длины
Определение критической нагрузки
Критическая нагрузка – это нагрузка, превышение которой вызывает потерю устойчивостипрямолинейной формы равновесия стержня. Критическую нагрузку обозначают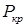 
. Можно утверждать, что достижение сжимающей нагрузкой критического значения равносильно разрушению стержня, так как неустойчивая прямолинейная форма равновесия неминуемо будет утрачена (стержень изогнется), что, приведет к практически неограниченному росту напряжений.
При потере устойчивости при превышении критической нагрузки прямолинейная ось стержня искривляется. Форма потери устойчивости - конфигурация изогнутой оси стержня. Форма потери устойчивости зависит от условий закрепления стержня и места приложения сжимающей нагрузки по его длине.
Л. Эйлер получил формулу для определения теоретической нагрузки (Эйлерова нагрузка), при которой происходит потеря устойчивости стержня. Формула Эйлера: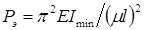 
, где Е – модуль Юнга; 
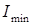– минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости); 
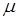– коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение 
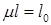- приведенная длина стержня.
ФОРМУЛА ЭЙЛЕРА ДЛЯ ШАРНИРНО-ОПЕРТОГО СТЕРЖНЯ, СЖАТОГО ПО КОНЦАМ
Для шарнирно опертого стержня, сжатого по концам, формула Эйлера для определения критической нагрузки: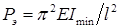 
(коэффициент приведения длины 
).
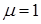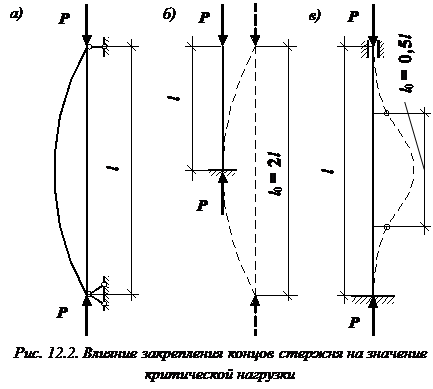Основной случай потери устойчивости – случай, когда при закреплении концов стержня и приложении нагрузки форма потери устойчивости представляет собой одну полуволну синусоиды (рис. 12.2, а).
Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по торцам) легко могут быть приведены к основному случаю потери устойчивости путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.
ФОРМУЛА ЭЙЛЕРА ДЛЯ СТЕРЖНЯ С ЗАЩЕМЛЕННЫМ И СВОБОДНЫМ КОНЦАМИ
При потере устойчивости стержень с жестко защемленным одним и свободным другим концом изогнется, как показано на (рис. 12.2, б). Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Приведенная длина равна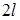 
(полуволна синусоиды имеет длину 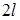), а эйлерова сила в четыре раза меньше, чем для основного случая. Формула Эйлера для стержня с защемленным и свободным концами: 
.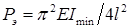