Статическая задача для толстостенной трубы
Расчет толстостенных труб
 В толстостенных трубах, нагруженных равномерным давлением, напряжения и деформации не изменяются вдоль оси трубы. При этом распределение напряжений и деформаций происходит одинаково во всех плоскостях, перпендикулярных к этой оси. По граням малого криволинейного элемента, выделенного в поперечном сечении трубы (рис. 5.5.1), действуют нормальные напряжения – радиальные σr и окружные σθ. Каждая точка трубы при ее деформации получает радиальное перемещение u. Величины напряжений σr и σθ, а также перемещения u зависят от расстояния r от рассматриваемой точки трубы до ее оси.
В толстостенных трубах, нагруженных равномерным давлением, напряжения и деформации не изменяются вдоль оси трубы. При этом распределение напряжений и деформаций происходит одинаково во всех плоскостях, перпендикулярных к этой оси. По граням малого криволинейного элемента, выделенного в поперечном сечении трубы (рис. 5.5.1), действуют нормальные напряжения – радиальные σr и окружные σθ. Каждая точка трубы при ее деформации получает радиальное перемещение u. Величины напряжений σr и σθ, а также перемещения u зависят от расстояния r от рассматриваемой точки трубы до ее оси.
Если сплошная (не составная) труба с внутренним радиусом а и наружным радиусом b не имеет днищ и нагружена равномерным внутренним ра и наружным рb давлением, то величины σr, σθ и u определяются по формулам Ламе
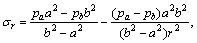
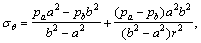
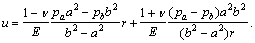
Поскольку в точках толстостенных труб реализуется сложное (плоское) напряженное состояние, оценка прочности их производится на основе тех или иных критериев (теорий) прочности.
Формулы Ламе используются, в частности, при расчете составных труб (рис. 5.5.2). В соответствии с решением А.В. Гадолина основные геометрические и силовые параметры таких труб определяются по формулам:
 радиальный натяг:
радиальный натяг: 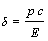 , (5.5.2)
, (5.5.2)
внешний радиус внутренней трубы: 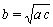 , (5.5.3)
, (5.5.3)
давление от натяга: 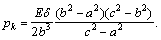 (5.5.4)
(5.5.4)
Условие прочности в наиболее напряженных точках составной трубы в соответствии с критерием наибольших касательных напряжений (III теория прочности) имеет вид
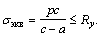 (5.5.5)
(5.5.5)
Функция напряжения
Дальнейшее сокращение неизвестных будем рассматривать при отсутствии объемных сил. Дифференциальные уравнения равновесия принимают вид
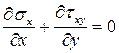 ,
,
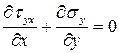
Так как в два дифференциальных уравнения равновесия входят три неизвестных напряжения, то, очевидно, что сами напряжения зависят от одной функции – функции напряжений Эри 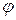 . Если напряжения выразить через функцию напряжений по формулам Эри:
. Если напряжения выразить через функцию напряжений по формулам Эри:
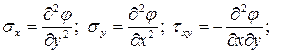
то дифференциальные уравнения равновесия удовлетворяются автоматически. Покажем, что первое уравнение равновесия выполняется. Для этого возьмем производные от формул Эри
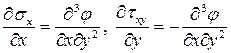
Суммируя левые и правы части этих равенств, получим
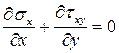 ,
,
т.е. первое дифференциальное уравнение равновесия выполняется. Аналогично, покажем, что и второе уравнение выполняется. Берем производные формул Эри, входящие во второе уравнение равновесия
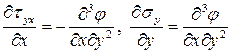
Подставляя эти производные во второе уравнение, получаем тождество.
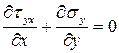
Таким образом, показано, что дифференциальные уравнения равновесия выполняются автоматически, если напряжения искать через функцию напряжений по формулам Эри.
