Основы схем из функциональных элементов. Проблема минимизации

Элементы функциональной полноты в классе двоичных функций.

1.1 Основные двоичные функции и их своства……………………..…………………….2

1.2 Утверждение о числе функций от n переменных……………………………………9

1.3 Представление функции в виде совершенной дизъюнктивной и совершенной конъюнктивной формах. Разложение функции по начальному множеству переменных…………………………………………………………………………………..13

1.4 Утверждение о представлении двоичной функции в виде полинома Жегалкина…………………………………………………………………………………..…19

1.5 Основные замкнутые классы двоичных функций относительно суперпозиций функций………………………………………………………………………………………...25

1.6 Критерий полноты в класее двоичных функций относительно суперпозиций функций…………………………………………………………………………………….…..31

1.7 Предполные классы двоичных функций……..…………………………………….….41

2. Минимизация ДНФ представляющих заданную функцию…………………………..55

2.1 Геометрическая интерпретация двоичных функций…………………………….…..57

2.2 Утверждение о максимальных интервалах и тупиковых покрытиях……………..60

2.3 Метод поиска всех максимальных интервалов заданной функции с помощью операции склеивания и поглащения……………………………………………………….63

2.4 Метод нахождения всех тупиковых покрытий максимальными интервалами….66

2.5 Метод построения сокращённой д.н.ф. с помощью обобщенного склеивания …..70

3. Элементы математической логики. Исчисление высказываний, его полнота…….72

4. Элементы теории графов………………………………………………………………….81

Неориентированные, ориентированные графы. Способы задания графов.

Матрица смежности, матрица инцендентностей, список смежности…………………..81

4.2 Азбука теории графов. Маршрут, путь, простой путь. Цикл. Простой цикл. Связность в графе……………………………………………………………………………..85

4.3 Методы анализа графа. Поиск в ширину. Нахождение кратчайших путей в графе……………………………………………………………………………..…….………88

Поиск в глубину. Нахождение остовного дерева с помощью поиска в

глубину……………………………………………………………………………………91

4.5 Укладки графов. Планарные графы. Теорема Эйлера инварианта планарного

гафа………………………………………………………………………………………..97

Критерий Понтрягина- Куратовского

панарности графов………………………..…………………………………………….100

4.7 Хроматическое число графа……………………………………………………….101

Элементы комбинаторики.

5.1 Упорядоченные наборы с повторением и без повторений…………………………106

5.2 Неупорядоченные наборы 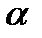элементов из 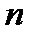данных без повторений………….109

5.3 Неупорядоченные наборы 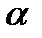элементов из п данных 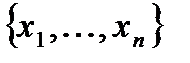с возможными повторениями……………..…………………………………………………………………110

5.4 Метод включения-исключения……………………………………………………….116

5.5 Основы метода производящих функций……………………………………………...119

5.6Основы теории перечисления Пойа. Лемма Бернсайда………………………..…...121

Основы схем из функциональных элементов. Проблема минимизации

схемы заданной функции…………………………………………………………………..131

6.1 Сложность мультиплексора порядка 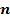……………………………………………….136

6.2 Сложность дешифратора порядка n…………………………………………………..137

6.3 Сложность универсального многополюсника……………………………………….137

6.4 Оценка сложности функций n переменных…………………………………………138

7. Элементы теории конечных автоматов……………………………………………….142

7.1 Ограниченно- детерминированные функции и автоматные языки. Эквивалентность…………………………………………………………………………….144

7.2 Схемы автоматов. Полнота логического базиса и задержки……………………...146

8. Элементы теории кодирования…………………………………………………………151

8.1 Критерий однозначности кодирования……………………………………………….152

8.2 Критерий префиксного кодирования Мак-Миллана……………………………….153

9. Задачи для практик……………………………………………………………………….157

Литература……………………………………………………………………164

Введение

В данном методическом пособии рассматриваются вопросы, входящие в университетский курс по дискретной математике. Большой раздел посвящён проблемам полноты булевых функций. В нём изложены основные определения и результаты по данной проблематике: теорема о представлении булевой функции в виде совершенной дизъюнктивной (конъюнктивной) нормальной формы, полинома Жегалкина, критерий Поста полноты, базисы в предполных классах. Следующий раздел посвящён проблемам минимизации представления булевых функций в виде ДНФ: геометрическая интерпретация, покрытия, интервалы, метод построения сокращённой и минимальных ДНФ. В заключение излагаются основы классического исчисления высказываний: основные определения, теорема дедукции, полнота исчисления высказываний.

Все разделы снабжены большим количеством учебных примеров и задач.

Пособие создано на основе программы первого семестра курса лекций по дискретной математике, читавшегося в Волгоградском государственном университете.