Краткие теоретические сведения. Дифференцирующей цепью называется линейный четырехполюсник

Дифференцирующей цепью называется линейный четырехполюсник, напряжение на выходе которого пропорционально первой производной входного напряжения:

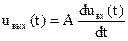, (1)

где A — постоянная величина, имеющая размерность времени.

Интегрирующей цепью называется линейный четырехполюсник, напряжение на выходе которого пропорционально интегралу входного напряжения:

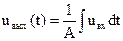. (2)

Дифференцирование и интегрирование может быть осуществлено при помощи цепей из последовательно соединенных индуктивности и активного сопротивления (цепи RL) или последовательно соединенных емкости и активного сопротивления (цепи RC), при выполнении определенных условий в отношении постоянных времени этих цепей. Наибольшее распространение получили дифференцирующие и интегрирующие цепи RC, так как конденсатор по сравнению с катушкой индуктивности имеет меньшую стоимость.

2.1. Дифференцирующая цепь.

На рис. 1 изображена RС дифференцирующая цепь.

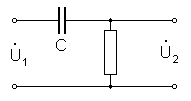
Рис. 1

Коэффициент передачи дифференцирующей цепи равен

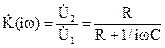, (3)

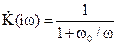или , (4)

где w₀=1/RC. Модуль коэффициента передачи, называемый амплитудно-частотной характеристикой, равен

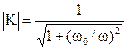. (5)

При частоте w=w₀ активное и реактивное сопротивления цепи равны и модуль коэффициента передачи равен 1/(2)^1/2. Фазочастотная характеристика дифференцирующей цепи равна

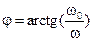. (6)

На рис. 2 показаны частотные характеристики дифференцирующей цепи. В области частот RCw<<1 коэффициент передачи равен 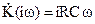. Из теории операционного исчисления известно, что это соответствует дифференцированию входного напряжения сигнала, т. е. выходное напряжение пропорционально первой производной входного сигнала с коэффициентом пропорциональности RC.

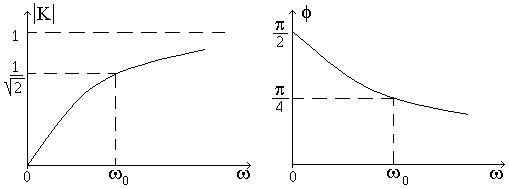
Рис. 2

Переходной характеристикой называют отклик цепи, т. е. напряжение на выходе при подаче на вход единичного скачка напряжения. Используя преобразование Лапласа, нетрудно показать, что переходная характеристика любой дифференцирующей цепи имеет вид при t³0

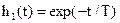, (7)

где Т=RC — постоянная времени.

Предположим, что на вход цепи подано переменное напряжение U₁ в виде двухполярных прямоугольных импульсов (рис. 3) длительностью Т/2 (Т-период). Тогда напряжение на выходе цепи U₂ будет изменяться по закону (рис. 3):

при 0<t<T/2 ,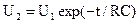

при T/2<t<T .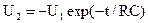

Если длительность полупериода Т/2 равна RC, то напряжение в конце каждого экспоненциального спада равняется 0,37U₁.

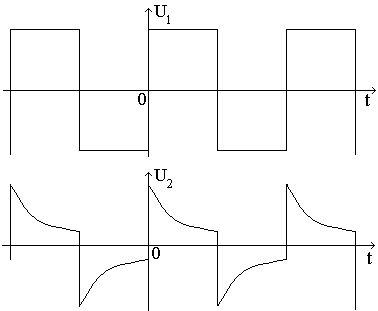
Рис. 3

2.2. Интегрирующая цепь.

На рис. 4 показана схема RC интегрирующей цепи.

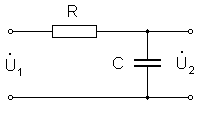
Рис. 4

Коэффициент передачи равен

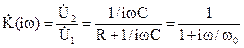, (8)

где w₀=1/RC соответствует частоте, при которой активное и реактивное сопротивления интегрирующей цепи равны. Выражения для амплитудно-частотной и фазочастотной характеристик имеют вид

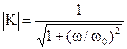, (9)

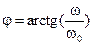. (10)

В области частот RCw>>1 коэффициент передачи имеет вид

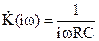, (11)

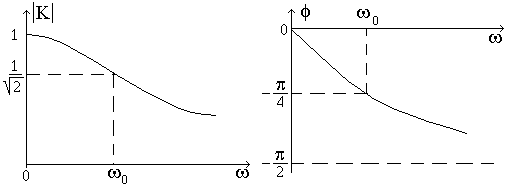что соответствует операции интегрирования. На рис. 5 приведены частотные характеристики интегрирующей цепи.

Рис. 5

Переходная характеристика интегрирующей цепи равна

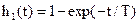, (12)

где T=RC — постоянная времени цепи. Предположим, что на вход цепи подано переменное напряжение U₁ в виде двухполярных прямоугольных импульсов (рис. 5) длительностью Т/2 (Т-период).

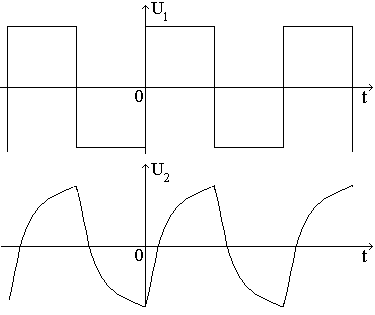
Рис. 6

Тогда напряжение на выходе цепи U₂ будет изменяться по закону (рис. 5):

при 0<t<T/2 ,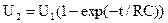

при T/2<t<T .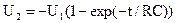

При Т/2=RC напряжение U₂ в моменты времени, кратные Т/2 и Т, равно по модулю |0,63U₁|.