Метод хорд и касательных

Постановка задачи. Дано нелинейное уравнение, где функция определена и непрерывно-дифференцируема для всех , причем функция меняет знак на концах этого отрезка т.е. .

Найти приближенное решение данного уравнения с точностью .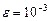

Приближенное решение и погрешность приближения находятся по следующей схеме:

если на , то

, , ;

, , ;

если на , то

, , ;

, , .

Приближенное решение и погрешность приближения :

, .

Лабораторная работа № 1

Тема: Решение нелинейных уравнений. Метод половинного деления.

Задание: 1) Отделить корни уравнения графически и программно .

2) Уточнить корни (все!) уравнения методом половинного деления с точностью 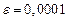, указать число разбиений отрезка.

Вопросы самоконтроля.

1) Как отделяются корни уравнения?

2) Какой должна быть величина шага при отделении корней?

3) Какие условия должны быть выполнены для применения метода половинного деления отрезка?

4) Какова идея метода половинного деления отрезка? Геометрическая иллюстрация.

5) Как вычисляется приближенный корень уравнения и какова его погрешность?

6) Как зависит погрешность результата от выбора приближенного решения?

1) ;

2) ;

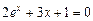3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) ;

13) ;

14) ;

15) ;

16) ;

17) ;

18) ;

19) ;

20) ;

21) ;

22) ;

23) ;

24) ;

25) ;

26) ;

27) ;

28) ;

29) ;

30) ;

31) ;

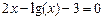32) ;

33) ;

34) ;

35) ;

36) ;

37) ;

38) ;

39) ;

40) ;

41) ;

42) ;

43) ;

44) ;

45) ;

46) ;

47) ;

48) ;

49) ;

50) ;

51) ;

52) ;

53) ;

54) ;

55) ;

56) ;

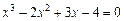57) ;

58) ;

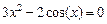59) ;

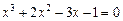60) .

Образец выполнения лабораторной работы № 1

(Решение нелинейных уравнений. Метод половинного деления.)

Постановка задачи. Найти корень нелинейного уравнения методом итерации с точностью .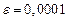

Решение задачи. Отделим корень уравнения на отрезке 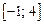графическим методом. Для этого табулируем функцию 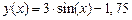на данном отрезке.

Имеем , , , ,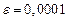

Выделим отрезок 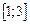содержащий изолированный корень, для уточнения которого применим метод половинного деления по схеме , , где , . Полагая , , а так же условие остановки деления отрезка пополам , составим таблицу

						корень	погрешность	Условие остановки
1,00000000	3,00000000	2,00000000	1,29583687	-1,17168626	0,15888308		1,00000000	нет
2,00000000	3,00000000	2,50000000	0,15888308	-1,17168626	-0,48776781		0,50000000	нет
2,00000000	2,50000000	2,25000000	0,15888308	-0,48776781	-0,15924305		0,25000000	нет
2,00000000	2,25000000	2,12500000	0,15888308	-0,15924305	0,00119806		0,12500000	нет
2,12500000	2,25000000	2,18750000	0,00119806	-0,15924305	-0,07868831		0,06250000	нет
2,12500000	2,18750000	2,15625000	0,00119806	-0,07868831	-0,03866032		0,03125000	нет
2,12500000	2,15625000	2,14062500	0,00119806	-0,03866032	-0,01870977		0,01562500	нет
2,12500000	2,14062500	2,13281250	0,00119806	-0,01870977	-0,00875050		0,00781250	нет
2,12500000	2,13281250	2,12890625	0,00119806	-0,00875050	-0,00377488		0,00390625	нет
2,12500000	2,12890625	2,12695313	0,00119806	-0,00377488	-0,00128807		0,00195313	нет
2,12500000	2,12695313	2,12597656	0,00119806	-0,00128807	-0,00004492		0,00097656	нет
2,12500000	2,12597656	2,12548828	0,00119806	-0,00004492	0,00057659		0,00048828	нет
2,12548828	2,12597656	2,12573242	0,00057659	-0,00004492	0,00026584		0,00024414	нет
2,12573242	2,12597656	2,12585449	0,00026584	-0,00004492	0,00011046		0,00012207	нет
2,12585449	2,12597656	2,12591553	0,00011046	-0,00004492	0,00003277	2,12591553	0,00006104	да
2,12591553	2,12597656	2,12594604	0,00003277	-0,00004492	-0,00000608	2,12594604	0,00003052	да
2,12591553	2,12594604	2,12593079	0,00003277	-0,00000608	0,00001335	2,12593079	0,00001526	да

Приближенное решение , погрешность , число итераций .

Следовательно, приближенное значение корня равно .

Запишем приближенное значение корня только верными значащими цифрами в узком смысле.

Имеем , , 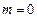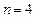. Округлим до 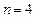. Получим , , .

Найдем число верных знаков для. . Имеем , , 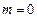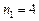. Так как 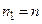, то получим приближенное значение корня с числом верных знаков .

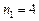Ответ: .