Дифференциальных уравнений

ЦЕЛЬ ЛЕКЦИИ: Дать постановку задачи численного решения системы обыкновенных дифференциальных уравнений с начальными условиями; провести классификацию численных методов по виду разностной схемы; ввести понятия локальной и интегральной точности, устойчивости по отношению к шагу интегрирования; построить простейший явный одношаговый метод, оценить его локальную погрешность, устойчивость к шагу интегрирования; пояснить свойство жесткости дифференциальных уравнений и непригодность для их решения классических явных методов.

Общая характеристика численных методов.

Пусть требуется решить систему обыкновенных дифференциальных уравнений (СОДУ)

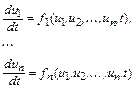
с начальными условиями

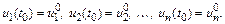
Это значит, что необходимо найти функции 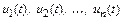на отрезке 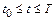такие, что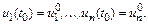

Запишем сформулированную задачу, ее называют задачей Коши для системы обыкновенных дифференциальных уравнений, в векторном виде:

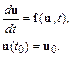
Решение задачи Коши заключается в нахождении такой траектории 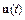, которая бы удовлетворяла условию .

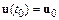Применение численных методов для решения задачи Коши предполагает приближенное вычисление значений 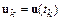в точках 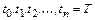отрезка . С этой целью СОДУ заменяют разностной схемой, из которой рекуррентно вычисляют приближенные значения .

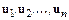Запишем общий вид разностной схемы:

.

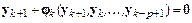Она связывает искомое решение 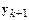в текущий момент времени 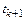с построенными к этому моменту времени решениями 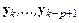в предыдущие моменты времени. Здесь 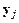– приближенное значение 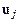, т. е. 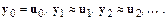Выбор функции 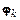в разностной схеме определяет соответствующий численный метод.

Приведем общую характеристику методов.

· Если 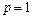, т. е.

,

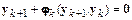то метод является одношаговым. Он связывает решение в последующий момент времени с решением в предыдущий момент времени. Если 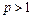, то метод является многошаговым.

· Метод является явным, если функция 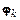не зависит от 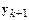и неявным в противном случае. В случае явного одношагового метода искомое решение 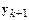на текущем шаге интегрирования вычисляется тривиально:

.

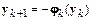Неявный одношаговый метод требует для расчета 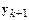решать систему в общем случае нелинейных алгебраических уравнений

,

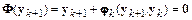привлекая, например, итерационную процедуру Ньютона.

· Различают локальную 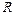и интегральную 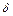погрешности метода. Локальная погрешность – ошибка на шаге интегрирования, интегральная погрешность – полная погрешность в текущий момент времени.

Обратимся к графической иллюстрации погрешности. Пусть численно решается уравнение

.

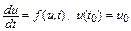В результате выполнения первого шага интегрирования (см. рис. 10.1) приближенное значение искомой функции в момент времени 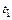равно

Рис. 10.1. Иллюстрация локальной и интегральной погрешностей

. Это значение принадлежит некоторой интегральной кривой 2, являющейся решением дифференциального уравнения при другом, отличном от 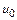, начальном условии. Разница между приближенным значением и точным 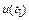составляет локальную погрешность. Очевидно, что на первом шаге локальная погрешность совпадает с интегральной погрешностью. Второй шаг интегрирования приводит к приближенному значению 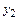, которое принадлежит интегральной кривой 3. Видно, что локальная погрешность на этом шаге, равная разности 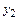и значения ординаты кривой 2 в момент времени 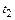, существенно отличается от интегральной погрешности – разности между приближенным 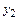и точным 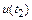значениями.

Наиболее объективной характеристикой точности метода является величина интегральной погрешности. К сожалению, выполнить ее оценку крайне сложно. На практике при выборе шага интегрирования обычно используют локальную погрешность численного метода.

· Если величина шага интегрирования 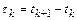ограничивается только допустимой локальной погрешностью 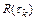метода, то такой метод является абсолютно устойчивым к шагу интегрирования. Метод, обладающий таким свойством, позволяет осуществлять выбор шага интегрирования, исходя лишь из требуемой точности. Условно устойчивый метод характеризуется тем, что шаг интегрирования ограничивается не только допустимой локальной погрешностью, но и определенными свойствами решаемой системы. Последние ограничения являются весьма обременительными для некоторых классов задач.

Рассмотрим разностные схемы наиболее широко используемых на практике методов численного интегрирования.

Явный метод Эйлера.

Рассмотрим 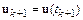, где 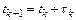, 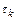– текущий шаг интегрирования. Разложим функцию 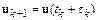в ряд Тейлора в окрестности точки :

.

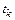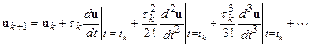Ограничившись в этом разложении двумя членами, получим разност-ную схему метода Эйлера

.

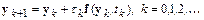Локальная погрешность метода Эйлера составляет величину

.

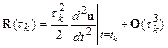В вычислительной математике численные методы решения обык-новенных дифференциальных уравнений принято характеризовать порядком точности.

Определение. Если локальная погрешность численного метода 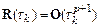,то порядок точности такого метода равен .

Метод Эйлера является методом первого порядка.

Приведем геометрическую интерпретацию явного метода Эйлера для задачи Коши

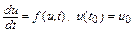
(см. рис. 10.2). Приращение на шаге интегрирования – катет прямоугольного треугольника, лежащий против угла, тангенс которого равен значению производной в предыдущий момент времени. Вторым катетом этого треугольника является текущий шаг интегрирования.

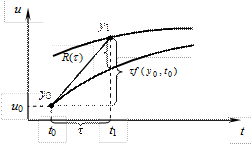
Рис. 10.2. Геометрическая иллюстрация явного метода Эйлера

Оценим устойчивость метода Эйлера по отношению к шагу ин-

тегрирования. Для этого рассмотрим линейную автономную систему

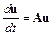
с отрицательно определенной матрицей 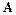простой структуры. Отрицательная определенность матрицы означает, что все собствен-ные значения 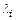матрицы действительны и отрицательны, т. е. 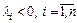. В этом случае все решения .

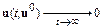Применим для решения этой системы метод Эйлера с постоянным шагом :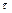

.

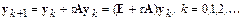Здесь E –единичная матрица соответствующей размерности.

Из алгебры известно, что для любой неособенной матрицы 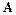простой структуры существует такая неособенная матрица 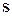, которая преобразованием подобия приводит матрицу 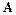к диагональному виду:

.

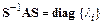Преобразуем вычислительную схему метода Эйлера следующим образом:

.

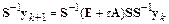Введем замену переменных 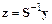. Тогда

,

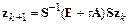или

.

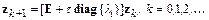Запишем это соотношение для i-й компоненты вектора :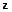

,

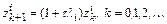или

,

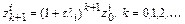где 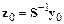, т. е. определяется начальным условием.

Нетрудно видеть, что

,

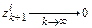если 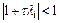. Именно этим свойством обладает решение автономной системы с отрицательно определенной матрицей. Отсюда приходим к требованиям

,

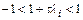при этом неравенство 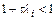приводит к естественному условию 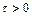, т. к. 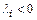, а неравенство 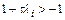- к условию

.

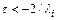Очевидно, чтобы 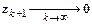, необходимо при выборе шага интегрирования выполнить условие

.

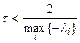Таким образом, явный метод Эйлера по отношению к шагу интегрирования является условно устойчивым.

Явление жесткости.

Ограниченная устойчивость численного метода является серьезным недостатком при решении так называемых жестких систем.

Рассмотрим дифференциальное уравнение первого порядка

,

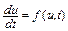для которого уравнение 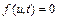имеет единственное решение

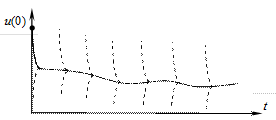
Рис. 10.3. К определению жесткости дифференциального уравнения

u

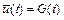. Любая интегральная кривая такого дифференциального уравнения характеризуется двумя участками с существенно различным поведением решения (см. рис. 10.3), причем первый участок значительно меньше второго. Первый участок с быстрым изменением функции отражает стремление интегральной кривой к графику функции 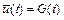и называется пограничным слоем. На втором участке интегральная кривая практически совпадает с графиком 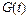. Однако даже при небольшом отклонении от графика 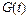в любой его точке производная 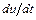резко возрастает по сравнению с производной 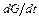. Именно по этой причине малый шаг интегрирования, используемый при воспроизведении быстропротекающего участка, не может быть существенно увеличен вне пограничного слоя в явных методах численного интегрирования.

Рассмотрим примеры жестких систем.

1. Простейшее дифференциальное уравнение

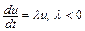(10.1)

может быть жестким (рис. 10.4) , если интервал наблюдения 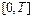зна-

Рис. 10.4. Семейство решений уравнения (10.1)

чительно превосходит величину 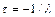. Решением такого уравнения является функция 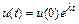. Пунктирные линии на рис. 10.4 соответствуют различным значениям .

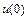2. Для иллюстрации явления жесткости дифференциальных уравнений может быть полезной также любая система линейных ОДУ, матрица которой характеризуется большим разбросом собственных значений, например система

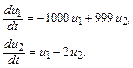(10.2)

Здесь собственные числа матрицы есть .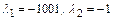

Решение этой системы (рис. 10.5)

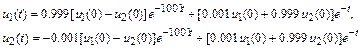
содержит быструю составляющую как для 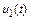, так и для 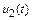, хотя по амплитуде быстрая составляющая функции 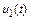значительно превосходит аналогичную компоненту функции 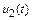(ее на рис. 10.5 в таком масштабе отобразить не удалось).

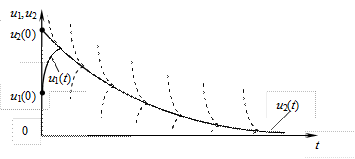
Рис. 10.5. Решение жесткой системы ОДУ (10.2)

Завершая краткую характеристику свойства жесткости дифференциальных уравнений, отметим, что при решении научных задач жесткость уравнений является скорее правилом, чем исключением. По этой причине для таких задач разработаны специальные методы численного интегрирования.

Лекция 11

Одношаговые методы

ЦЕЛЬ ЛЕКЦИИ: Построить простейший неявный одношаговый метод, обладающий свойством устойчивости к шагу интегрирования, оценить его локальную погрешность; дать способ Рунге–Кутта увеличения точности одношаговых методов, проиллюстрировав его методами второго и четвертого порядков точности; привести разностную схему линейных многошаговых методов, получить условия корректного выбора коэффициентов.

Неявный метод Эйлера.

Пусть требуется численно решить систему обыкновенных дифференциальных уравнений

.

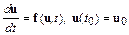Формально неявный метод Эйлера можно получить, рассматривая

,

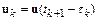где 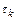– шаг интегрирования.

Разложим 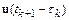в ряд Тейлора в окрестности точки :

.

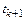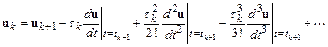Ограничившись в разложении двумя членами, придем к разностной схеме неявного метода Эйлера:

.

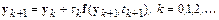Локальная погрешность при этом определяется отброшенными членами ряда Тейлора:

.

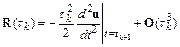Сравнивая явный и неявный методы Эйлера между собой (см. рис. 11.1), следует отметить, что методы обладают близкой по модулю, но разной по знаку погрешностью.

Рассмотрим устойчивость неявного метода Эйлера по отношению к шагу интегрирования. Применим его к системе уравнений

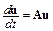
с отрицательно определенной матрицей 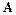, полагая шаг интегрирования 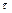постоянным:

.

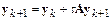Отсюда

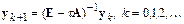
Пусть 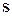– неособенная матрица, которая преобразованием подобия приводит матрицу 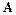к диагональному виду

.

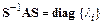Привлекая матрицу 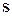, преобразуем итерационное правило следующим образом:

,

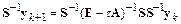или

,

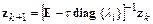где новая переменная

.

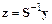Запишем результат для 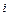-й компоненты вектора :

.

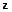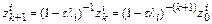Отсюда следует, что 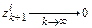при любом 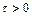, поскольку все .

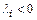Неявный метод Эйлера является абсолютно устойчивым по отношению к шагу интегрирования. При решении этим методом жестких систем дифференциальных уравнений шаг интегрирования выбирается только из соображений допустимой локальной погрешности.

Методы Рунге–Кутта.

Точность явных одношаговых методов численного решения систем обыкновенных дифференциальных уравнений вида

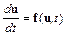
можно повысить, сохраняя в разложении функции 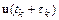в ряд Тейлора большее число членов. Например, метод второго порядка имеет следующую разностную схему:

,

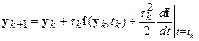или

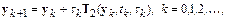
где

.

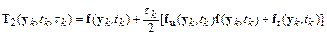Основное неудобство такой формы разностной схемы – необходимость вычисления частных производных 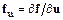, 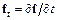. Эта трудность значительно возрастает при построении методов более высокого порядка точности.

В методах Рунге–Кутта функции 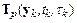, где 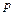– порядок точности метода, заменяются на некоторые удобно вычисляемые функции 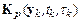таким образом, что

,

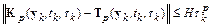где 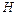– константа, не зависящая от .

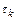В методе Рунге–Кутта второго порядка функция 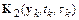имеет вид

.

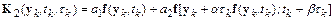Разложим функцию 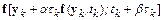в ряд Тейлора в окрестности точки :

.

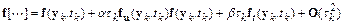Подставим это разложение в выражение для :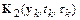

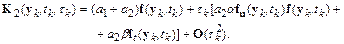
Сравнивая 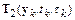и 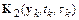, нетрудно видеть, что при

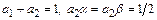
эти формы совпадают с точностью до члена .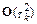

Если положить 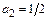, то 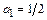, 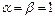. В результате метод Рунге–Кутта второго порядка примет вид:

,

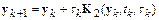где

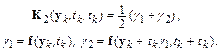
По аналогии можно построить методы Рунге–Кутта более высоких порядков. Не останавливаясь на выводе, приведем популярный на практике метод Рунге–Кутта четвертого порядка:

,

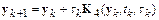где

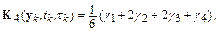
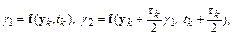
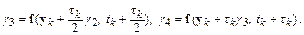
На каждом шаге интегрирования в методе Рунге–Кутта четвертого порядка приходится четырежды вычислять значение функции 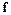при разных значениях аргументов. Более того, эти значения функции используются лишь однократно, что отражается на эффективности вычислений.

Методы Рунге–Кутта относятся к классу явных условно устойчивых методов. По этой причине они оказываются неприемлемыми для решения жестких систем обыкновенных дифференциальных уравнений.