Интегрирование тригонометрических функций
I.Интеграл вида 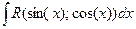 , где R(sin(x), cos(x)) – это рациональная функция относительно sin(x) и cos(x) подстановкой tg
, где R(sin(x), cos(x)) – это рациональная функция относительно sin(x) и cos(x) подстановкой tg 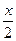 = t сводится к интегралу от рациональной функции относительно t.
= t сводится к интегралу от рациональной функции относительно t.
Действительно найдем.
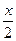 = arctg(t);
= arctg(t);
x = 2 arctg(t); dx = 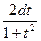 ;
;
sin(x) = sin2 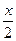 =
= 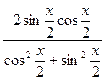 ;
;
разделим числитель и знаменатель на cos2 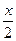 ; |tg
; |tg 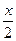 = t|
= t|
sin(x) = 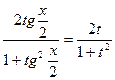 ;
;
cos(x) = 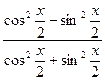 , делим на cos2
, делим на cos2 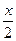 ;
;
cos(х) = 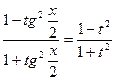 ; тогда
; тогда
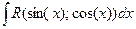 =
= 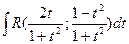 = ∫ r(t) dt, где r(t) – рациональная функция
= ∫ r(t) dt, где r(t) – рациональная функция
 относительно t.
относительно t.
r(t)
Пример: Вычислить.
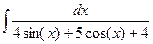 = | tg
= | tg 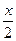 = t | =
= t | = 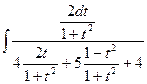 =
= 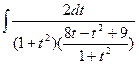 =
=
= 2 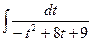 = -2
= -2 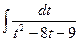 = -2
= -2 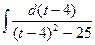 =
= 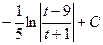 ;
;
Такая подстановка называется универсальной, т.е. она пригодна для вычислений интеграла sin(x) и cos(x).
Замеяание1: часто применение универсальной подстановки приводит к громоздким вычислениям. Некоторые интегралы могут быть решены другим способом.
а) ∫ R(sin(x))cos(x) dx = | sin(x) =t; cos(x)dx = dt | = ∫ R(t) dt.
∫ R(t) dt – интеграл от рациональной функции относительно t.
б) ∫ R(cos(x))sin(x) dx = – ∫ R(t) dt;
 в) ∫ R(tg(x)) dx = | tg(x)=t; x= arctg(t); dx = dt/(1+t2)| =
в) ∫ R(tg(x)) dx = | tg(x)=t; x= arctg(t); dx = dt/(1+t2)| = 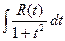 = ∫r(t)dt ,
= ∫r(t)dt ,
r(t)
где r(t)- рациональная функция относительно t.
Пример: вычислить интеграл.
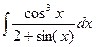 =
= 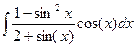 = |sin(x) = t ; cos(x)dx=dt| =
= |sin(x) = t ; cos(x)dx=dt| = 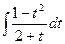 =
=

 = _-t2 +1 |t+2 =∫(2 – t –3/(t+2))dt = 2t – t2/2 – 3 ln|t+2| = 2 sin(x)-1/2sin2x –3ln|sin(x)+2|+C
= _-t2 +1 |t+2 =∫(2 – t –3/(t+2))dt = 2t – t2/2 – 3 ln|t+2| = 2 sin(x)-1/2sin2x –3ln|sin(x)+2|+C
- t2-2t -t+2
_ 2t+1
2t+4
-3
Замечание2: если подынтегральная функция содержит sin(x) и cos(x) в четной степени и произведение sin(x)cos(x), то целесообразней применять подстановку tg(x) = t, тогда
x = arctg(t), dx = 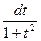 ;
;
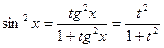 ;
;
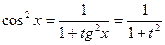 ;
;
sin(x)cos(x) = 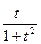 ;
;
В результате получается рациональная функция относительно t.
Пример: 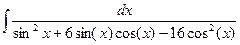 = | tg(x) = t ; dx =
= | tg(x) = t ; dx = 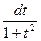 | =
| =
= 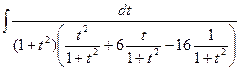 =
= 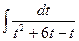 =
= 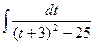 =
= 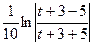 =
=
= 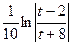 =
= 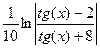 + C.
+ C.
II.Интеграл вида 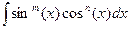
а)
I случай. m и n – положительные, одно из них нечетное.
Пусть m=2p+1 , тогда ∫sin2p(x)cosn(x) sin(x)dx = – ∫(sin2x) p cosn(x) d(cos(x)) =
= – ∫(1 –cos2x) p cosn(x) d(cos(x)).
II.случай. m и n – целые, положительные, четные.
Пусть m=2p, n=2q, тогда
∫sinm(x)cosn(x)dx = ∫sin2p(x)cos2q(x)dx = ∫(sin2x) p(cos2x) qdx = 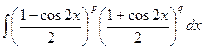 ;
;
Возводя скобки в соответствующие степени и разбивая интеграл на сумму интегралов, в результате получаем интегралы либо типа а), либо типа б).
III.случай. m + n = –2k; tg(x)=t; ctg(x)=t;
Пример1:
I.случай. ∫sin5(x)cos2(x)dx = ∫sin4(x)cos2(x)sin(x)dx = –∫(sin2x) 2cos2(x)d(cos(x)) =
= –∫(1 – cos2x) 2cos2(x)d(cos(x)) = –∫(cos2x – 2 cos4x + cos6x)d(cos(x)) = –∫cos2(x)d(cos(x)) +
+ 2 ∫cos4(x)d(cos(x)) –∫cos6(x)d(cos(x)) = – cos3(x)/3 + 2 cos5(x)/5 – cos7(x)/7 +C.
Пример2:
∫sin4(x)cos2(x)dx = 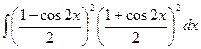 =
= 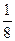 ∫(1 – cos2x)(1 – cos2(2x))dx =
∫(1 – cos2x)(1 – cos2(2x))dx =
= 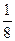 ∫(1 – cos2x)sin2(2x))dx =
∫(1 – cos2x)sin2(2x))dx = 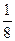 ∫sin2(2x))dx –
∫sin2(2x))dx – 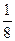 ∫cos2x∙sin2(2x))dx =
∫cos2x∙sin2(2x))dx = 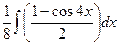 –
–
– 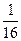 ∫sin2(2x))d(sin2x) =
∫sin2(2x))d(sin2x) = 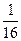 ∫dx –
∫dx – 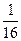 ∫cos(4x)dx –
∫cos(4x)dx – 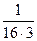 sin3(2x) =
sin3(2x) = 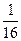 x –
x – 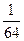 sin(4x) –
sin(4x) –
– 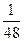 sin3(2x) + C.
sin3(2x) + C.
Пример3:
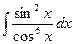 = ∫sin2(x)cos-6(x)dx = | m+n = 2-6 = 4| =
= ∫sin2(x)cos-6(x)dx = | m+n = 2-6 = 4| = 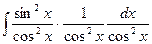 =
=
= ∫ tg2(x)( 1+tg2(x))d(tg(x)) = ∫ tg2(x)d(tg(x)) + ∫ tg4(x)d(tg(x)) = tg3(x)/3 + tg5(x)/5 + C.
Пример4:
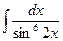 =
= 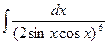 =
= 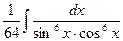 =
= 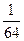 ∫ sin–6(x)cos–6(x) dx = | m=-6; n=-6; m+n=-12; | =
∫ sin–6(x)cos–6(x) dx = | m=-6; n=-6; m+n=-12; | = 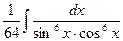 =
= 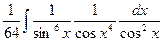 = =
= = 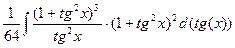 =
= 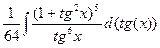 = |(1+x)n= 1 + nx +
= |(1+x)n= 1 + nx +
+ 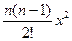 | =
| = 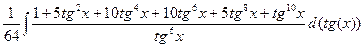 =
= 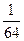 ∫ tg–6x d(tg(x)) +
∫ tg–6x d(tg(x)) +
+ 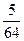 ∫ tg–4x d(tg(x)) +
∫ tg–4x d(tg(x)) + 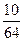 ∫ tg–2x d(tg(x)) +
∫ tg–2x d(tg(x)) + 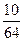 ∫ d(tg(x)) +
∫ d(tg(x)) + 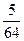 ∫ tg2x d(tg(x)) +
∫ tg2x d(tg(x)) +
+ 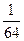 ∫ tg4x d(tg(x)) =
∫ tg4x d(tg(x)) = 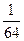 (
( 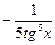
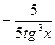
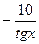 + 5 tg2(x) +
+ 5 tg2(x) + 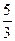 tg3(x)+
tg3(x)+ 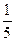 tg5(x)) + C.
tg5(x)) + C.
Интегралы, не выражающиеся через элементарные функции (не берущиеся).
1. 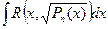 ,где Pn(x) – многочлен n-ой степени; не берется, если n выше 2-ой степени;при n = 2,3,4.. – интеграл эллиптического типа.
,где Pn(x) – многочлен n-ой степени; не берется, если n выше 2-ой степени;при n = 2,3,4.. – интеграл эллиптического типа.
2. 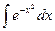 - интеграл Пуассона.
- интеграл Пуассона.
3. 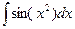 ;
; 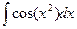 - интегралы Френеля.
- интегралы Френеля.
4. 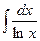 и сводящийся к нему
и сводящийся к нему 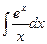 - интегральный логарифм.
- интегральный логарифм.
5. 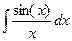 ;
; 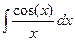 ; - интегральный синус, интегральный косинус.
; - интегральный синус, интегральный косинус.
Раздел II.
Определенный интеграл.
