Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Рассмотрим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами

y′′ + py′ + qy = f(x),

где p и q – постоянные коэффициенты, f(x) - правая часть уравнения, имеющая специальный вид.

Общее решение дифференциального уравнения представляет собой сумму общего решения y_общсоответствующего однородного уравнения и частного решения y_чнеоднородного уравнения.

Рассмотрим случай, когда f(x) имеет специальный вид f(x) = P_n(x) 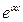, где P_n(x) – многочлен степени n, a – действительное число. В этом случае частное решение неоднородного дифференциального уравнения ищется как

y_ч = x^rQ_n(x) ,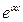

где r – число равное кратности a как корня характеристического уравнения k² + pk + q = 0, Q_n(x) – многочлен степени n с неопределенными коэффициентами, которые нужно найти.

@ Задача 3. Найти общее решение дифференциального уравнения: .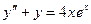

Решение: Сначала находим общее решение однородного дифференциального уравнения. Характеристическое уравнение k² + 1 = 0 имеет корни i и – i. Общее решение однородного дифференциального уравнения имеет вид y_общ = c₁cosx + c₂sinx. Корни характеристического уравнения не совпадает с a = 1, поэтому r = 0. Частное решение неоднородного дифференциального уравнения ищется в виде y_ч = (Ax + B) 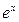. Для нахождения A и B это решение подставляется в неоднородное дифференциальное уравнение. Ax + 2A + B + Ax + B = 4x, откуда A = 2, B = – 2. Частное решение имеет вид y_ч = 2(x – 1)e^x. Общее решение неоднородного дифференциального уравнения равно

y = c₁cosx + c₂sinx + 2(x – 1) e^x.

Рассмотрим случай, когда f(x) = 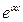(P_n(x)cosβx + Q_m(x)sinβx), где P_n(x) и Q_m(x) – многочлены степени n и m, α и β - действительные числа. В этом случае частное решение неоднородного дифференциального уравнения ищется в виде

y_ч = x^r 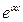(M(x)cosβx + N(x)sinβx),

где M(x) и N(x) многочлены степени max(m, n).

§3.9. Числовые ряды

Числовые ряды

Числовым рядом называется бесконечная сумма чисел 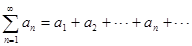(1),

где 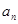- общий член ряда.

Конечная сумма чисел 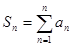называется частичной суммой ряда.

Если S_n стремится к конечному пределу S, то говорят, что ряд сходится, а предел называется суммой ряда. Если предел ряда не существует или 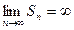, то говорят, что ряд расходится.

! Пример: Числовой ряд 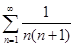сходится и сумма равна S = 1. Ряд с a_n = n расходится. Ряд с a_n = (– 1)ⁿ тоже расходится.

Свойства рядов

1. Если ряд (1) сходится и его сумма равна S, то ряд 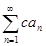также сходится и его сумма равна cS.

2. Если ряд (1) и ряд 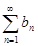сходятся, то сходятся также их сумма и разность.

3. Если к ряду (1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1) сходятся или расходятся одновременно.