ДЕ7.Дифференциальные уравнения

Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений 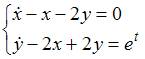имеет вид …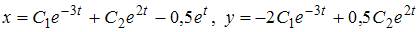

Решение:
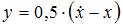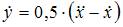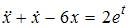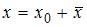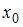Решим систему дифференциальных уравнений методом исключения. Из первого уравнения находим , откуда После подстановки во второе уравнение системы получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами Общее решение этого уравнения имеет вид где общее решение соответствующего однородного уравнения, а 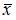некоторое частное решение неоднородного уравнения.
Характеристическое уравнение 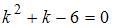имеет два действительных корня 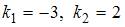.Таким корням соответствует общее решение однородного дифференциального уравнения 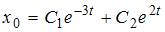.Поскольку правая часть исходного уравнения 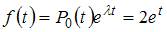, то имеем уравнение со специальной правой частью.
Так как 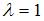не является корнем характеристического уравнения, то частное решение 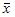неоднородного уравнения будем искать в виде 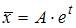Найдя производные первого и второго порядков и подставив в уравнение 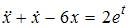, получим 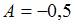Тогда общее решение исходного уравнения имеет вид 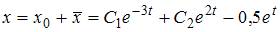Дифференцируя полученное решение, находим 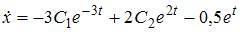и 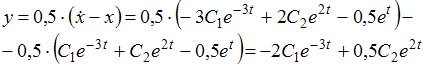Значит, общее решение системы уравнений имеет вид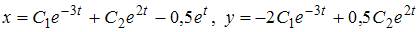

Тема: Поле направлений и изоклины
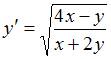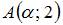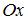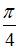Дано дифференциальное уравнение . Тогда отрезок соответствующего ему поля направлений в точке образует с осью угол при 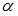равном 2.

Решение:
Так как дифференциальное уравнение имеет вид 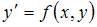, то угол 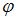определяется из равенства 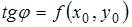, где 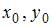-координаты точки А.

В рассматриваемом случае 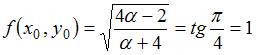,то есть 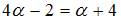. Следовательно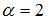

Тема: Дифференциальные уравнения с разделяющимися переменными
Общее решение дифференциального уравнения 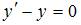имеет вид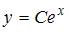

Решение:
Разделим переменные: 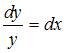. Проинтегрируем обе части уравнения: 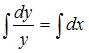Тогда 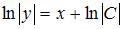.Откуда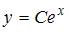

Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения 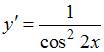, удовлетворяющее условию 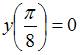, имеет вид …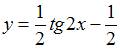

Решение:
Проинтегрируем обе части уравнения: 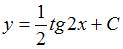. Подставив условие 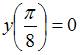, получим 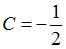и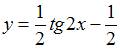

Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений 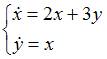имеет вид…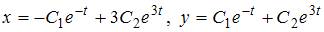

Решение:
Решим систему дифференциальных уравнений методом исключения.
Из второго уравнения находим производную 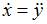и после подстановки выражений для 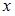и 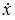в первое уравнение системы получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами 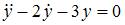Характеристическое уравнение 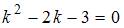имеет два действительных корня: 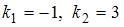Таким корням соответствует общее решение однородного дифференциального уравнения 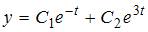.Дифференцируя полученное решение, находим 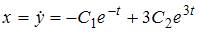Тогда общее решение системы уравнений имеет вид .

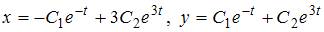Тема: Поле направлений и изоклины
Поле направлений дифференциального уравнения 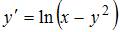определяется неравенством …

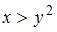Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение 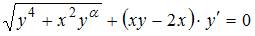будет уравнением с разделяющимися переменными при значении 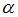, равном….. 4.

Решение:
Данное уравнение можно представить в виде 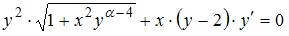. Это уравнение будет уравнением с разделяющимися переменными при 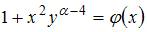, то есть при 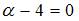, откуда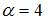

Тема: Задача Коши для дифференциального уравнения первого порядка
Решение задачи Коши 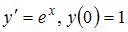имеет вид …..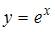

Решение:
Проинтегрировав обе части уравнения, получим: 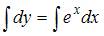. Тогда общее решение исходного уравнения имеет вид .
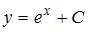Для вычисления значения 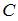подставим в найденное общее решение начальное условие 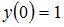. Тогда 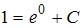и .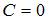
Следовательно, частное решение имеет вид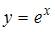

Тема: Дифференциальные уравнения с разделяющимися переменными
Общее решение дифференциального уравнения 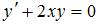имеет вид …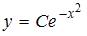

Решение:
Разделим переменные: 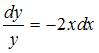. Проинтегрируем обе части уравнения: 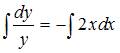. Тогда 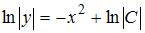, откуда

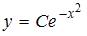
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений 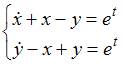имеет вид …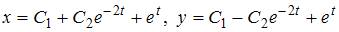

Решение:
Решим систему дифференциальных уравнений методом исключения.
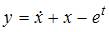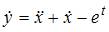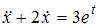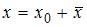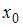Из первого уравнения находим , откуда . После подстановки во второе уравнение системы получим линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами .Общее решение этого уравнения имеет вид , где – общее решение соответствующего однородного уравнения, а 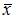– некоторое частное решение неоднородного уравнения. Характеристическое уравнение 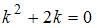имеет два действительных корня: 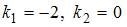. Таким корням соответствует общее решение однородного дифференциального уравнения 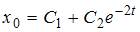. Поскольку правая часть исходного уравнения 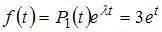, то имеем уравнение со специальной правой частью.
Так как 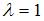не является корнем характеристического уравнения, то частное решение 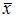неоднородного уравнения будем искать в виде .
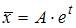Найдя производные первого и второго порядков и подставив в уравнение
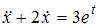, получим 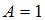. Тогда общее решение исходного уравнения имеет вид .
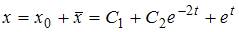Дифференцируя полученное решение, находим 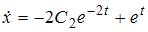и .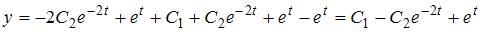
Следовательно, общее решение системы уравнений имеет вид .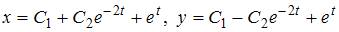

Тема: Поле направлений и изоклины
Дано дифференциальное уравнение 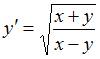. Тогда отрезок соответствующего ему поля направлений в точке 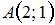образует с осью 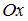угол, равный …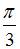

Решение:
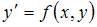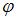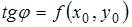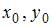Так как дифференциальное уравнение имеет вид , то искомый угол определяется из равенства , где – координаты точки .
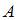В рассматриваемом случае 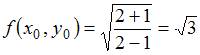, то есть 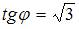. Следовательно,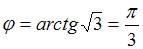

Тема: Задача Коши для дифференциального уравнения первого порядка
Решение задачи Коши 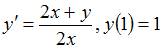, имеет вид …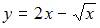

Решение:
Сделаем замену 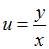. Тогда 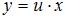, 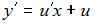и уравнение запишется в виде 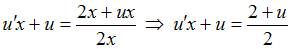. Разделив переменные, получим: 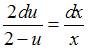. Проинтегрируем обе части последнего уравнения: .
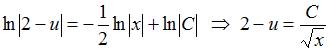Сделаем обратную замену: 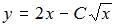; подставим в найденное общее решение начальное условие 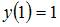. Тогда 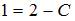и .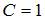
Следовательно, частное решение имеет вид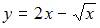

Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение задачи Коши 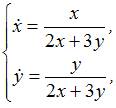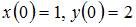, имеет вид …

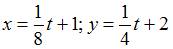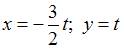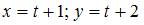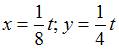Решение:
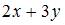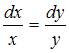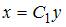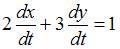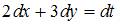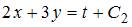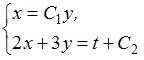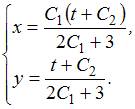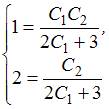
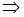
Выразив из первого уравнения, можем получить , откуда . Сложив удвоенное первое и утроенное второе уравнения, получим , или , то есть . Из системы уравнений находим общее решение системы Подставив начальные условия, получим: 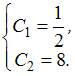.Поэтому решение задачи Коши имеет вид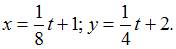

Тема: Поле направлений и изоклины
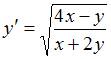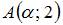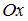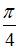Дано дифференциальное уравнение . Тогда отрезок соответствующего ему поля направлений в точке образует с осью угол при 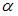равном…

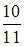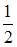Решение:
Так как дифференциальное уравнение имеет вид 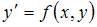, то угол 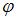определяется из равенства 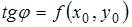, где 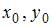– координаты точки .
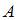В рассматриваемом случае 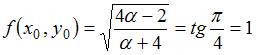, то есть 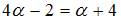. Следовательно,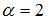

Тема: Поле направлений и изоклины
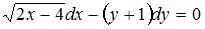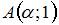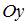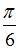Дано дифференциальное уравнение . Тогда отрезок соответствующего ему поля направлений в точке образует с осью угол при 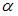равном …

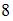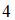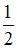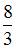Решение:
Данное уравнение можно представить в виде 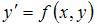. Действительно, 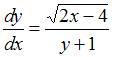, или 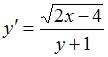. Тогда угол 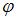определяется из равенства 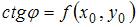, где 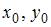– координаты точки .
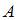В рассматриваемом случае 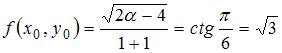, то есть 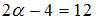. Следовательно,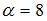

Тема: Задача Коши для дифференциального уравнения первого порядка
Функция 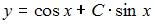является общим решением дифференциального уравнения 1-го порядка. Тогда для начального условия 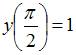частное решение этого уравнения имеет вид …

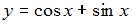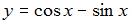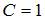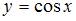Решение:
Подставив в общее решение начальное условие 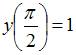, то есть 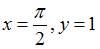, получим значение .
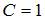Следовательно, искомое частное решение имеет вид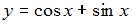

Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение задачи Коши 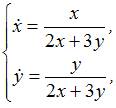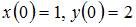, имеет вид …

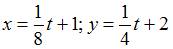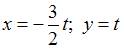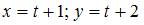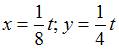Тема: Поле направлений и изоклины
Дано дифференциальное уравнение 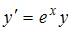. Тогда отрезок соответствующего ему поля направлений в точке 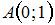образует с осью 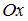угол, равный …

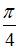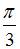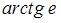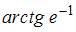Решение:
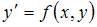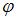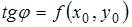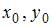Так как дифференциальное уравнение имеет вид , то искомый угол определяется из равенства , где – координаты точки 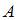. В рассматриваемом случае 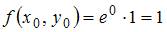, то есть .
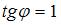Следовательно, .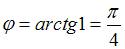

Тема: Задача Коши для дифференциального уравнения первого порядка
Решение задачи Коши 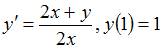, имеет вид …

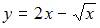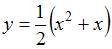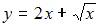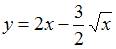Решение:
Сделаем замену 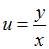. Тогда 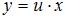, 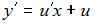и уравнение запишется в виде 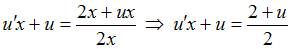. Разделив переменные, получим: 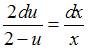. Проинтегрируем обе части последнего уравнения: .
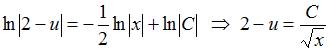Сделаем обратную замену: 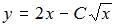; подставим в найденное общее решение начальное условие 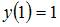. Тогда 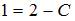и .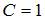
Следовательно, частное решение имеет вид .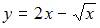

Тема: Дифференциальные уравнения с разделяющимися переменными
Общее решение дифференциального уравнения 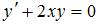имеет вид …

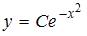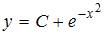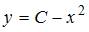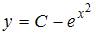Решение:
Разделим переменные: 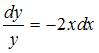. Проинтегрируем обе части уравнения: 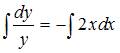. Тогда 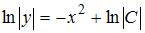. Откуда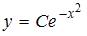

Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение задачи Коши 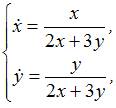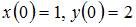, имеет вид …

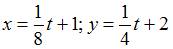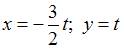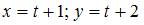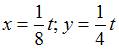Тема: Дифференциальные уравнения с разделяющимися переменными
Общее решение дифференциального уравнения 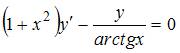имеет вид …

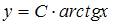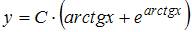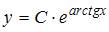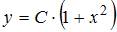Решение:
Разделим переменные: 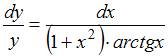. Проинтегрируем обе части уравнения: 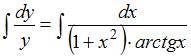. Тогда 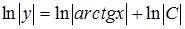. Откуда .

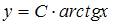Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения 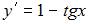, удовлетворяющее условию 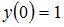, имеет вид …

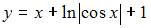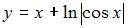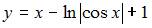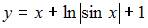Решение:
Проинтегрируем обе части уравнения: 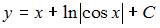. Подставив начальное условие 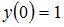, получим 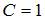и .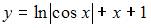

Тема: Поле направлений и изоклины
Поле направлений дифференциального уравнения 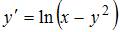определяется неравенством …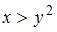

Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений 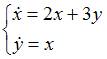имеет вид …

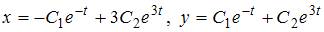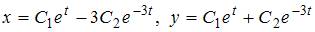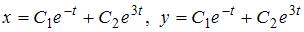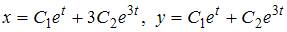Решение:
Решим систему дифференциальных уравнений методом исключения.
Из второго уравнения находим производную 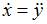и после подстановки выражений для 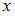и 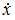в первое уравнение системы получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами .
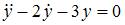Характеристическое уравнение 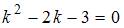имеет два действительных корня: .
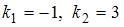Таким корням соответствует общее решение однородного дифференциального уравнения 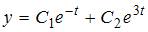. Дифференцируя полученное решение, находим .
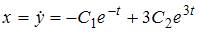Тогда общее решение системы уравнений имеет вид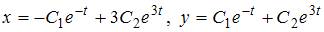

Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения 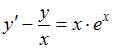, удовлетворяющее условию 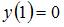, имеет вид …

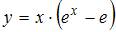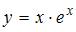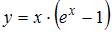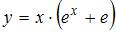Решение:
Введем замену 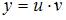; 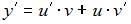. Тогда уравнение 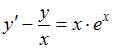примет вид 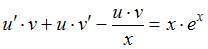, или .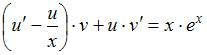
Пусть 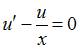. Тогда 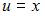. Подставим найденное значение 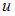в уравнение 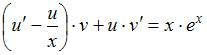. Получим: 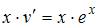, то есть 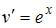и .
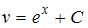Общее решение примет вид 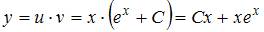. Подставив начальное условие, получим .
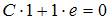Откуда 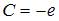и частное решение будет иметь вид .

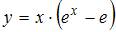Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений 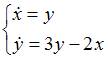имеет вид …

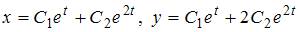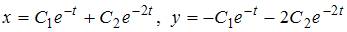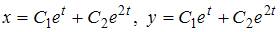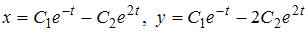Решение:
Решим систему дифференциальных уравнений методом исключения.
Из первого уравнения находим производную 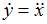и после подстановки выражений для 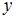и 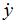во второе уравнение системы получим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами 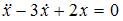. Характеристическое уравнение 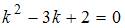имеет два действительных корня: .
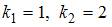Таким корням соответствует общее решение однородного дифференциального уравнения .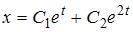
Дифференцируя полученное решение, находим .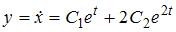
Тогда общее решение системы уравнений имеет вид .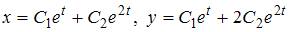

Тема: Дифференциальные уравнения с разделяющимися переменными
Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …

			,
			,
			,

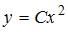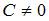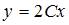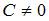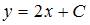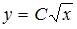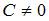Решение:
Угловой коэффициент касательной в произвольной точке равен производной в этой точке, то есть 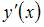, а угловой коэффициент радиус-вектора точки касания определяется отношением 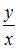. Тогда для нахождения уравнения искомой кривой получим уравнение с разделяющимися переменными 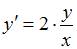. Разделив переменные, получим 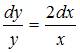. Проинтегрируем обе части этого уравнения: 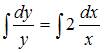. Тогда 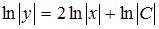, 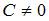. Откуда , .

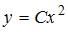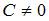Тема: Поле направлений и изоклины
Дано дифференциальное уравнение 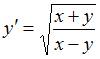. Тогда отрезок соответствующего ему поля направлений в точке 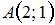образует с осью 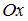угол, равный …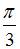

Тема: Дифференциальные уравнения с разделяющимися переменными
Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …

			,
			,
			,

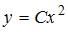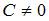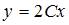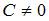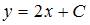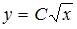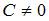Решение:
Угловой коэффициент касательной в произвольной точке равен производной в этой точке, то есть 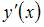, а угловой коэффициент радиус-вектора точки касания определяется отношением 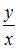. Тогда для нахождения уравнения искомой кривой получим уравнение с разделяющимися переменными 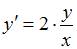. Разделив переменные, получим 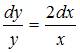. Проинтегрируем обе части этого уравнения: 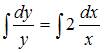. Тогда 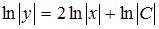, 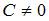. Откуда , .

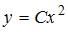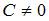Тема: Задача Коши для дифференциального уравнения первого порядка
Частное решение дифференциального уравнения 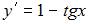, удовлетворяющее условию 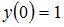, имеет вид …