Раздел 3. Контрольные задания

Задание 1. Задача о распределении ресурсов. Симплексный метод.

Вариант выдается преподавателем по списку

Для производства двух видов продукции А и В используются материалы трех сортов.

На изготовление единицы изделия А (В) расходуется соответственно а₁ (в₁) кг материала 1-го сорта, а₂ (в₂) кг материала 2-го сорта, а₃ (в₃) кг материала 3-го сорта.

Всего имеется с₁ , с₂ , с₃ , кг материалов 1-го сорта, 2-го сорта, 3-го сорта.

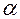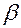Реализации единицы продукции А (В)приносит прибыль соответственно и ( ) рублей.

Построить экономико-математическую модель задачи.

Определить графическим методом, при каком объеме производства каждого вида продукции прибыль будет максимальной.

Решить задачу аналитически симплексным методом. Сделать экономический анализ полученного решения.

Решить задачу в EXCEL с использованием надстройки «Поиск решения». Приложить распечатку результатов (3-х отчетов), проанализировать её.

Решить задачу в пакете Simplex. Приложить распечатку результатов.

Составить двойственную задачу и получить ее решения, опираясь на теоремы двойственности.

Как изменится прибыль, если запас материала 1-го сорта увеличится на 100 кг?

Вариант
А1
А2
А3
В1
В2
В3
С1
С2
С3
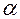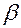Вариант
А1
А2
А3
В1
В2
В3
С1
С2
С3
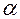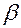Вариант
А1
А2
А3
В1
В2
В3
С1
С2
С3
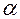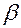Вариант
а1
а2
а3
в1
в2
в3
с1
с2
с3
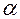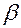Вариант
а1
а2
а3
В1
В2
В3
С1
С2
С3

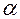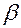Задание 2 . Транспортная задача. Метод потенциалов

Вариант выдается преподавателем по списку

На трех складах имеются минеральные удобрения в количестве а₁, а₂, а₃ тонны (см. табл.1). Потребности четырех бригад в минеральных удобрениях соответственно в₁, в₂, в₃, в₄ тонн (см. табл. 1). Расстояния в километрах между складами и бригадами даны в матрице расстояний D и являются одинаковыми для всех вариантов:

5 2 4 9

D = 2 3 5 7

8 1 3 6

Критерий оптимальности – минимальный объем грузоперевозок в т/км.

Таблица 1

Вариант	Запасы удобрений на складах, т	Потребности бригад в удобрениях, т
а1	а2	а3	в1	в2	в3	в4