Пара несимметричных двойственных задач

Пара двойственных задач может также быть несимметричной. Несимметричная пара двойственных задач удовлетворяет следующим условиям:

1. Матрицы систем ограничений задач транспонированы по отношению к друг другу.

2. Каждому ограничению одной задачи соответствует переменная во второй задаче; при этом переменная, соответствующая ограничению-неравенству в одной задаче, удовлетворяет условию неотрицательности в другой, а переменная, соответствующая ограничению-равенству, может быть любого знака.

3. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами соответствующих ограничений другой. При этом свободные члены целевых функций задач совпадают.

4. Целевые функции задач оптимизируются противоположным образом, то есть если одна из задач - на максимум, то вторая - на минимум, а если одна из задач на минимум, то вторая - на максимум.

5. Если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³».

6. Во всех ограничениях задач свободные члены находятся в правой части, а члены с переменными - в левой.

Наконец, условия 1 - 6 называются условиями двойственности.

Таким образом, симметричная и несимметричная пары двойственных задач отличаются только 2-м условием.

Пример 1. Составить двойственные к задачам:

а) 2x₁+2x₂-5x₃ ® max(min); б) 2x₁+2x₂-5x₃ ® min

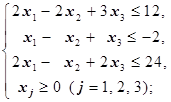
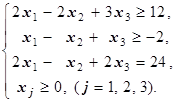
Решение. а) Сначала составим двойственную к задаче на максимум (max). Двойственная - следующая:

12y₁-2y₂+24y₃ ® min

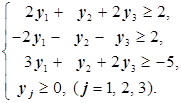
Покажем, что действительно получили двойственную задачу. Для этого покажем, что для пары

2x₁+2x₂-5x₃ ® max 12y₁-2y₂+24y₃ ® min

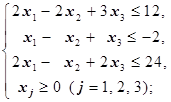
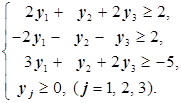
задач выполнены все условия двойственности.

1. Матрицы систем ограничений задач транспонированы по отношению к друг другу:

= .

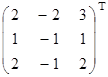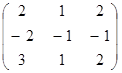2. В каждой задаче по три ограничения и три переменные, то есть каждому ограничению одной задачи соответствует переменная в другой задаче. При этом все переменные одной задачи соответствуют ограничениям-неравенствам другой, и поэтому удовлетворяют условиям неотрицательности.

3. Коэффициенты 2, 2, -5 при переменных в целевой функции первой задачи являются свободными членами соответствующих ограничений второй и, наоборот, коэффициенты 12, -2, 24 при переменных в целевой функции второй задачи являются свободными членами соответствующих ограничений первой. При этом свободные члены целевых функций задач совпадают (оба равны 0).

4. Целевые функции задач оптимизируются противоположным образом: исходная задача - на максимум, а вторая - на минимум.

5. Выдержаны требования к соответствию типа экстремума целевой функции к типам неравенств в ограничениях: если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³».

Теперь составим двойственную к задаче на минимум (min). Тогда исходную необходимо переписать согласно виду экстремума целевой функции - минимума. Это означает, что все нетривиальные неравенства в исходной задаче должны принять вид «³». Для этого достаточно эти неравенства умножить на -1:

а) 2x₁+2x₂-5x₃ ® min

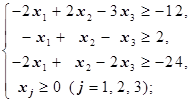
Двойственная - следующая:

-12y₁+2y₂-24y₃ ® max

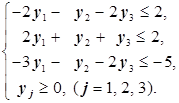
Убеждаемся в этом точно так же, как и в предыдущем случае.

б) Двойственная - следующая:

12y₁-2y₂+24y₃ ® max

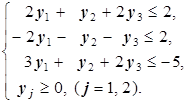
Покажем, что действительно получили двойственную задачу. Для этого покажем, что для пары

2x₁+2x₂-5x₃ ® min 12y₁-2y₂+24y₃ ® max

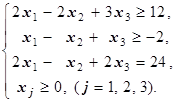
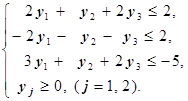
задач выполнены все условия двойственности.

1. Матрицы систем ограничений задач транспонированы по отношению к друг другу:

=

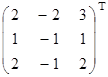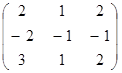
2. В каждой задаче по три ограничения и три переменные, то есть каждому ограничению одной задачи соответствует переменная в другой задаче. При этом переменные x₁, x₂, x₃, y₁, y₂, соответствующие ограничениям-неравенствам в одной задаче, удовлетворяет условиям неотрицательности в другой, а переменная y₃, соответствующая ограничению-равенству в первой, может быть любого знака (на неё ограничение неотрицательности не накладывается).

3. Коэффициенты 2, 2, -5 при переменных в целевой функции первой задачи являются свободными членами соответствующих ограничений второй и, наоборот, коэффициенты 12, -2, 24 при переменных в целевой функции второй задачи являются свободными членами соответствующих ограничений первой. При этом свободные члены целевых функций задач совпадают (оба равны 0).

4. Целевые функции задач оптимизируются противоположным образом: исходная задача - на минимум, а вторая - на максимум.

5. Выдержаны требования к соответствию типа экстремума целевой функции к типам неравенств в ограничениях: если целевая функция задачи максимизируется, то знаки неравенств в ограничениях задачи имеют вид «£», а если минимизируется, то имеют вид «³».

Во всех ограничениях задач свободные члены находятся в правой части, а члены с переменными - в левой.