Как производится расчет простейших статически неопределимых балок?

Он может быть произведен, например, с использованием универсального уравнения упругой линии балки (другой из возможных способов приводится в беседе 15). Рассмотрим, например, один раз статически
неопределимую балку (рис. 7.17).

Для определения трех реактивных усилий мы имеем пока только два уравнения статики:

Третье дополнительное уравнение, необходимое для раскрытия статической неопределимости, можно получить, записав условия равенства нулю прогиба на шарнирной опоре: .

При , то есть в заделке, прогиб 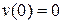и угол поворота сечения . Поэтому условие отсутствия прогиба в точке B может быть представлено в виде:

или

.

Теперь мы имеем систему из трех уравнений с тремя неизвестными:

;

;

.

Решая ее, находим:

,

Таким образом, статическая неопределимость балки нами раскрыта.

ГИПОТЕЗЫ ПРОЧНОСТИ

Прежде всего, отметим, что в настоящей беседе речь будет идти об оценке прочности не всего тела, а о прочности материала в отдельно взятой его точке. Напомним, что в случае линейного НС оценка прочности в исследуемой точке тела довольно легко производится путем непосредственного сопоставления возникающего в ней расчетного напряжения либо с предельным 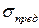, либо с допускаемым напряжением .

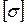Коэффициент запаса прочности равен отношению предельного напряжения к расчетному: .

Состояние материала, при котором хотя бы в одной точке тела отмечено возникновение текучести или признаков хрупкого разрушения, рассматривается как предельное,то естьсоответствующее началу нарушения прочности всего тела. Соответствующее этому состоянию напряжение называется предельным.

Для пластичных материалов за предельное напряжение принимается предел текучести , а для хрупких – предел прочности .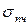

Расчет на прочность, основанный на таком представлении о предельном состоянии тела, называется расчетом по опасной точке или расчетом по допускаемым напряжениям.

В современной практике, однако, применяют и другие методы расчета, например, по предельным нагрузкам или несущей способности, по расчетным предельным состояниям и т. д. Эти методы основаны на иных представлениях о предельных состояниях тела. В настоящем пособии эти методы не рассматриваются.

Напомним также, что мы будем отдавать предпочтение терминам «предельное состояние» и «предельное напряжение», вместо терминов «опасное состояние» и «опасное напряжение», которые используются в некоторых учебниках по сопротивлению материалов.

8.1. Как подойти к оценке прочности материала в общем случае нагружения, то есть при объемном НС?

Разнообразие НС безгранично и создать каждое из них в лабораторных условиях для определения предельного состояния для всех материалов невозможно как по техническим, так и по экономическим причинам.

Поэтому желательно иметь практическую возможность оценки прочности определенного материала, находящегося в условиях любого сложного НС,располагая при этом только ограниченными опытными данными о его свойствах, например, только значениями предельных напряжений при одноосном растяжении и сжатии.

Это становится возможным при применении так называемых гипотез прочности (или теорий предельных НС).

Будем называть два НС эквивалентными, если они одновременно переходят в предельные при увеличении соответствующих им главных напряжений в одно и то же число раз. Это означает, что коэффициенты запаса прочности для эквивалентных НС одинаковы.

Остается решить вопрос, что же является критерием эквивалентности различных по характеру НС. Если решение этого вопроса каким-то образом найдено (его как раз и дают гипотезы прочности), тогда для расчета стержня на прочность в случае сложного НС его следует заменить на эквивалентное одноосное растяжение (сжатие) и сравнить соответствующее ему эквивалентное напряжение с предельным (или допускаемым) напряжением для данного материала.

Этот подход к оценке прочности при объемном НС иллюстрируется условной схемой, показанной на рис. 8.1.

8.2.
Какой смысл вкладывается в понятие «эквивалентное напряжение»?

Из приведенных рассуждений следует, что эквивалентное напряжение – это лишь некоторая воображаемая условная расчетная величина, а не какое-то реально возникающее напряжение. Значение эквивалентного напряжения зависит не только от заданного типа НС (то есть от значений, соответствующих ему главных напряжений), но и от принятого для расчета прочности критерия эквивалентности НС. Поэтому, в частности, нельзя говорить, что эквивалентное напряжение возникает в некоторой точке. Следует говорить об определении (или вычислении) эквивалентного напряжения для исследуемой точки.

8.3. Что называется гипотезами прочности?

Гипотезы, указывающие критерии эквивалентности различных НС, называют гипотезами прочности.

Приведем и другие, используемые в учебниках по сопротивлению материалов, названия: теории предельных напряженных состояний, теории прочности и т. д.

Как следует из изложенного, применение гипотез прочности избавляет нас от необходимости проведения огромного количества экспериментов. Тот или иной критерий эквивалентности может быть основой для практических расчетов на прочность лишь при условии, что для ряда частных случаев он проверен опытным путем и результаты эксперимента оказались достаточно близкими к результатам теоретического расчета.

Определение истинной причины разрушения материала является труднейшей задачей. Это обстоятельство не позволило до настоящего времени создать единую общую гипотезу прочности и повлекло за собой появление многих теорий, каждая из которых основывается на своей гипотезе о причине разрушения материала.

Независимо от принятой гипотезы прочности условие прочности после определения эквивалентного напряжения представляется в виде одного из следующих неравенств:

или, при заданном коэффициенте запаса,

.

8.4. Как формулируется первая гипотеза прочности? И какие опытные данные подтверждают ее справедливость?

Первая гипотеза прочности основывается на предположении о том, что причиной разрушения материала являются наибольшие по абсолютномузначению нормальные напряжения.

Эту, самую простую и старую, гипотезу, предложенную еще Галилеем, называют гипотезой наибольших нормальных напряжений.

Условие прочности по первой гипотезе прочности имеет вид:

. (8.1)

В случае, когда наибольшим по абсолютному значению будет сжимающее главное напряжение , условие (8.1) записывается в виде:

.

Существенный недостаток первой гипотезы виден из приведенных выше двух формул. Заключается он в том, что при определении эквивалентного напряжения совершенно не учитываются два других главных напряжения, оказывающих, естественно, большое влияние на прочность материала.

Эта гипотеза подтверждается экспериментальными данными только для хрупкого материала и только при растяжении, когда главные напряжения значительно меньше, чем .

При всестороннем сжатии, например, цементного кубика она приводит к ошибочным результатам, поскольку кубик выдерживает напряжения, во много раз превышающие предел прочности при одноосном сжатии.

В настоящее время эта гипотеза прочности не применяется и имеет лишь историческое значение.

8.5. Что является причиной разрушения по второй гипотезе прочности?

Отмеченные недостатки первой гипотезы прочности привели к появлению второй гипотезы прочности, предложенной Мариоттом и затем развитой Сен-Венаном.

Согласно этой гипотезе, называемой гипотезой наибольших линейных деформаций, причиной разрушения являются наибольшие линейные деформации. Условие прочности по этой гипотезе записывается в виде:

,

где 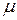– коэффициент Пуассона.

Отметим следующее. Вторая гипотеза прочности предполагает, что для пластичных материалов закон Гука выполняется вплоть до предела текучести, а для хрупких – до предела прочности, что, конечно, является чересчур грубым допущением.

Достоинством же этой гипотезы является то, что при вычислении эквивалентного напряжения она учитывает все три главных напряжения.

С помощью этой гипотезы можно объяснить разрушение хрупких материалов при простом сжатии. Однако, как и первая гипотеза, вторая гипотеза прочности недостаточно подтверждается опытами и поэтому в настоящее время не применяется.

8.6. Как формулируется третья гипотеза прочности?

Согласно этой гипотезе, которую называют также гипотезой наибольших касательных напряжений, причиной разрушения материала являются наибольшие касательные напряжения.

Линии Людерса, разрушение по наклонной плоскости образца из хрупкого материала, образование воронки при разрыве – все это указывает на большую роль, которую играют касательные напряжения.

Согласно третьей гипотезе, максимальное касательное напряжение для заданного объемного НС и эквивалентного ему линейного НС одинаковы, то есть

.

Напомним, что в случае объемного НС наибольшее касательное напряжение определяется по формуле

. (8.2)

Эквивалентное напряжение при одноосном растяжении равно:

. (8.3)

С учетом формул (8.2) и (8.3), условие прочности по третьей гипотезе прочности принимает вид:

.

Недостатком этой гипотезы является то, что она не учитывает второго главного напряжения .

Опыты показывают, что для пластичных материалов гипотеза наибольших касательных напряжений дает удовлетворительные результаты. Ошибка от пренебрежения влиянием не превышает обычно 10 – 15 %.

Третья гипотеза прочности впервые была высказана Кулоном. Критерий наибольших касательных напряжений был предложен им в 1773 г. Условие наступления пластического состояния впервые выдвинул в 1868 г. французский инженер Анри Эдуард Треска (Treska, 1814 – 1885 гг.). Затем это условие было математически сформулировано Сен-Венаном.

8.7. В чем заключается смысл энергетической (четвертой) гипотезы прочности?

Энергетическая гипотеза прочности строится на предположении о том, что количество удельной потенциальной энергии изменения формы, накопленной к моменту наступления предельного состояния материала, одинаково как при сложном НС, так и при простом одноосном растяжении.

Необходимо обратить внимание Читателя на то, что в этой гипотезе речь идет не обо всей удельной потенциальной энергии деформации, а лишь о той ее части, которая накапливается за счет изменения формы кубика с ребром, равным единице. В общем случае полная удельная потенциальная энергия деформации может быть представлена как сумма энергий, связанных с изменением объема кубика и изменением его формы.

Условие прочности по четвертой гипотезе прочности приведем без вывода:

.

Очевидным достоинством этой теории является то, что эквивалентное напряжение определяется значениями всех трех главных напряжений.

Энергетическая гипотеза прочности хорошо согласуется с опытными данными для пластичных материалов. Для них она приводит к несколько лучшим результатам, чем гипотеза наибольших касательных напряжений.

Идею энергетического критерия прочности материала впервые предложил в 1856 г. английский ученый Джеймс Клерк Максвелл (Maxwell, 1831 – 1879 гг.). В 1885 г. ее развил итальянский ученый Эудженио Бельтрами (Beltrami, 1835 – 1900 гг.). В 1904 г. польский ученый Максимилиан Тытус Губер (Huber, 1872 – 1950 гг.) и в 1911 г. немецкий ученый Рихард Мизес (Mises, 1883 – 1953 гг.) завершили разработку этой теории прочности.

8.8. Как формулируется гипотеза прочности Мора?

Согласно этой гипотезе, которую в 1900 г. предложил немецкий ученый Отто Христиан Мор (Mohr, 1835 – 1918 гг.), два напряженных состояния равноопасны, если для соответствующих главных напряжений и соблюдается соотношение:

. (8.4)

Тогда условие прочности по гипотезе прочности Мора имеет вид:

. (8.5)

Из формулы (8.5) видно, что данная гипотеза прочности не учитывает влияния второго главного напряжения .

В (8.4) и (8.5) коэффициент представляет собой отношение предельных напряжений, соответствующих одноосным растяжению и сжатию, то есть этот коэффициент равен:

· для хрупких материалов

;

· для пластичных

.

Гипотеза прочности Мора может быть рекомендована для хрупких материалов. Для пластичных материалов она тождественна третьей гипотезе прочности.

КОСОЙ ИЗГИБ

9.1. Какой изгиб называется косым?

Если мы прикладываем к балке вертикальную нагрузку, а она при этом прогибается почему-то не только в вертикальной плоскости, но и вбок, то такой изгиб называется косым. Или, иными словами, косым называется изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости (плоскости, в которой расположены все внешние нагрузки).