Инейные разностные уравнения первого порядка
Пусть  – размер популяции в конце n – го периода времени. Предположим, что скорость роста популяции в любой период времени пропорциональна размеру популяции в начале этого периода. Если постоянную пропорциональности обозначить через а, то, учитывая, что прирост популяции выражается величиной
– размер популяции в конце n – го периода времени. Предположим, что скорость роста популяции в любой период времени пропорциональна размеру популяции в начале этого периода. Если постоянную пропорциональности обозначить через а, то, учитывая, что прирост популяции выражается величиной 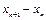 , получим:
, получим: 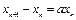 . Сгруппировав члены, приходим к разностному уравнению первого порядка
. Сгруппировав члены, приходим к разностному уравнению первого порядка
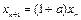 . (1.1)
. (1.1)
Пусть известен начальный размер популяции  . Тогда из уравнения (1.1) последовательно находим:
. Тогда из уравнения (1.1) последовательно находим:
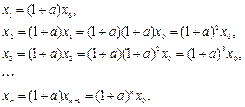
Таким образом, общее решение или общая формула для 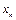 имеет вид:
имеет вид:
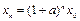 . (1.2)
. (1.2)
Если постоянная пропорциональности 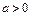 , то выполняется условие
, то выполняется условие 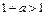 и, следовательно,
и, следовательно, 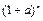 безгранично возрастает с ростом n. Отсюда следует, что
безгранично возрастает с ростом n. Отсюда следует, что 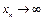 при
при 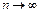 . Если
. Если 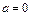 , то популяция остается на постоянном уровне
, то популяция остается на постоянном уровне  ,
, 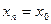 . Это случай нулевого роста. Если
. Это случай нулевого роста. Если 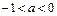 , то
, то 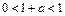 и
и 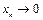 при
при 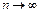 . Заметим, что при
. Заметим, что при 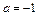 популяция вымирает после первого же периода времени. Значения
популяция вымирает после первого же периода времени. Значения 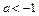 нас не интересуют, так как они приводят к отрицательным численностям.
нас не интересуют, так как они приводят к отрицательным численностям.
Пример 1.4. Популяция бактерий первоначально насчитывала 1000 особей и постоянно увеличивалась с темпом роста 50 % в каждый час. Какова численность популяции после 10 часов роста?
Решение. Пусть 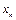 – численность популяции бактерий после n часов роста. По условию задачи,
– численность популяции бактерий после n часов роста. По условию задачи, 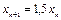 и
и  . Общее решение разностного уравнения есть
. Общее решение разностного уравнения есть 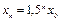 . По прошествии 10 часов размер популяции составит
. По прошествии 10 часов размер популяции составит 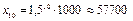 .
.
Рассмотренное выше уравнение 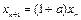 представляет собой пример линейного разностного уравнения первого порядка.
представляет собой пример линейного разностного уравнения первого порядка.
Определение 1.2. Линейным разностным уравнением первого порядка называется уравнение
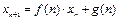 , (1.3)
, (1.3)
где 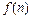 и
и 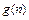 – заданные функции от n.
– заданные функции от n.
Если известно  , то по уравнению можно определить
, то по уравнению можно определить 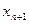 .
.
Если 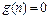 , то уравнение (1.3) называется однородным, и неоднородным – в противном случае
, то уравнение (1.3) называется однородным, и неоднородным – в противном случае 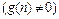 .
.
Рассмотрим однородное уравнение
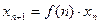 (1.4)
(1.4)
Считая в (1.4) 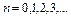 последовательно находим:
последовательно находим:
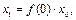
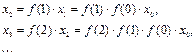
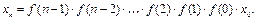 (1.5)
(1.5)
Формула (1.5) есть общее решение уравнения (1.4).
Пример 1.5. Рассмотрим популяцию бактерий, растущую от начального размера в 1000 особей таким образом, что ее размер по прошествии n+1 часов больше размера после n часов в 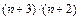 раза. Какова численность популяции после 10 часов роста?
раза. Какова численность популяции после 10 часов роста?
Решение. Пусть  – размер популяции после n часов роста. Известно, что
– размер популяции после n часов роста. Известно, что  и что
и что 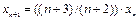 . Это разностное уравнение первого порядка при
. Это разностное уравнение первого порядка при 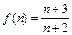 . Используя (1.5), имеем:
. Используя (1.5), имеем:
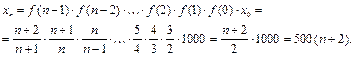
Размер популяции после 10 часов равен 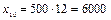 .
.
Рассмотрим теперь неоднородное уравнение (1.3). Считая 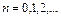 из уравнения (1.3) последовательно находим:
из уравнения (1.3) последовательно находим:
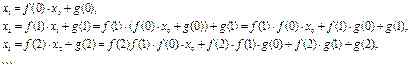
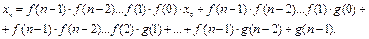 (1.6)
(1.6)
Формула (1.6) дает общее решение неоднородного уравнения (1.3).
Пример 1.6. Популяция бактерий растет от начального размера в 1000 особей таким образом, что ее прирост в интервале от n до n+1 часов с начала роста составляет 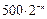 . Каков размер популяции после 10 часов роста?
. Каков размер популяции после 10 часов роста?
Решение. По условию, 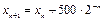 и
и  , где
, где  – размер популяции после n часов роста. Учитывая, что
– размер популяции после n часов роста. Учитывая, что 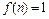 ,
, 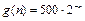 , находим:
, находим:
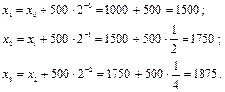
Общий вид решения таков:
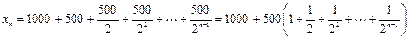 .
.
Выражение в скобках представляет собой сумму членов геометрической прогрессии с параметрами 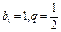 . Используя формулу
. Используя формулу 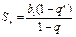 , получим:
, получим:
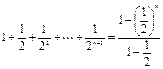 .
.
Итак, 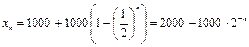 .
.
После 10 часов роста размер популяции составит
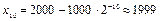 .
.
С течением времени размер популяции бактерий приближается к предельному, или равновесному, размеру, равному 2000.
