Применения степенных рядов.

18.2.6.3.1. Приближённое вычисление значений функций. Идея таких вычислений простая. Пусть известно значение функции в точке 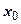, и функция разлагается в окрестности точки 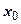в ряд Тейлора. Тогда значение функции в точке 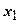, которое надо найти, равно 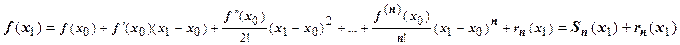, и принимается 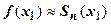. Естественно, мы должны гарантировать, что погрешность такого приближения не превышает заданной величины 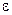. Погрешность равна остатку ряда после n-го члена (или остаточному члену формулы Тейлора), поэтому необходимо строить оценку сверху для 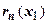(или ). 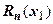При оценке 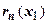принципиально отличны два случая. Если остаток - знакочередующийся ряд, то 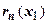просто оценивается по своему первому члену. Если остаток не является знакочередующимся рядом, то необходимо оценивать всю его сумму. Обычно в этом случае остаток мажорируют сходящейся геометрической прогрессией. В разделе 18.4.2. Знакочередующиеся рядымы рассмотрели и тот, и другой случай при нахождении значени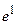й и 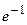; в разделе 7.9.2. Приближённые вычисления с помощью формулы Тейлораприведён пример вычисления значения 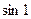с погрешностью 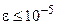. Другие примеры будут рассмотрены ниже.

Интегрирование функций.

1. Как мы знаем, интеграл 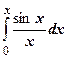аналитически не берётся. Это специальная функция, называемая интегральным синусом и обозначаемая 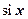. Получим разложение этой функции в степенной ряд. 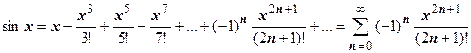, , 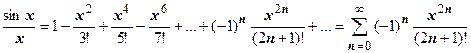почленно интегрируем: 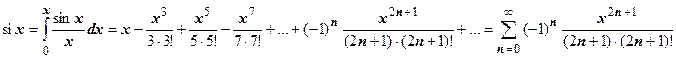. Ряд сходится к 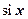при 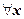. Теперь легко вычислить значение этой функции в любой точке. Пусть, например, надо найти 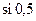с погрешностью 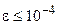. . 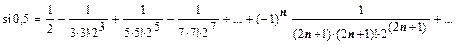Ряд знакочередующийся, первый член, меньший 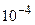, третий, поэтому .

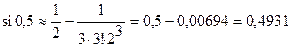2. Найти 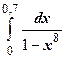. Этот интеграл берётся аналитически. Надо разложить знаменатель на множители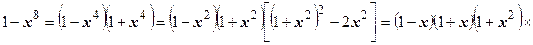

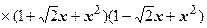, разложить подынтегральную функцию на пять простых дробей, найти восемь неопределённых коэффициентов и т.д., и после этого вычислять значение первообразной в начальной и конечной точках. Поступим по другому. Разложим подынтегральную функцию в ряд Маклорена и почленно проинтегрируем: 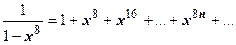, 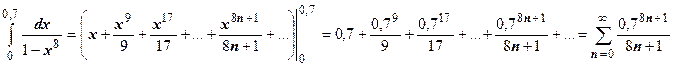. Остаток ряда после n-го члена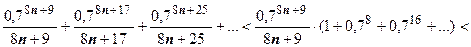 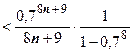. Если 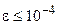, достаточно взять n=2, и .

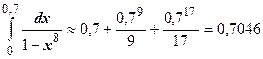18.2.6.3.3. Интегрирование дифференциальных уравнений с помощью степенных рядов. Пусть дана задача Коши: ,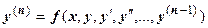

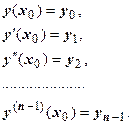
Решение этой задачи в виде ряда Тейлора ищется так. 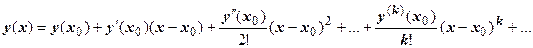. Первые n коэффициентов ряда известны из начальных условий, остальные находятся последовательным дифференцированием уравнения.

Примеры. 1. 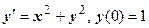. Из уравнения находим 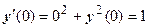. Дифференцируем уравнение: 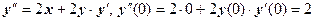. Далее дифференцируем уравнение и находим значение производной в точке 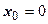: 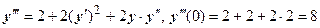, 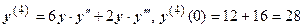. Так мы можем вычислить производные любого порядка. Решение задачи Коши: .

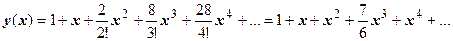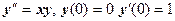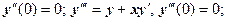
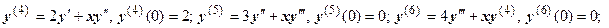
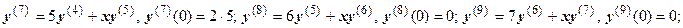
2. . Находим: 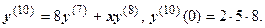Закономерность понятна. Производные порядка 3n-1 и 3n равны нулю, производная порядка 3n+1 равна 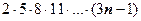, поэтому 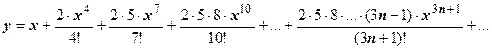С помощью признака Даламбера легко убедится, что этот ряд сходится при 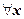, следовательно, даёт решение задачи Коши на всей числовой оси.