Теоретическое описание
Классическая электродинамика
Основная статья: Классическая электродинамика
В большинстве случаев макроскопические электромагнитные процессы с необходимой степенью точности могут быть описаны в рамках классической электродинамики. В этом случае взаимодействующие объекты рассматриваются как совокупность материальных точек, характеризуемых помимо массы также и электрическим зарядом. При этом полагается, что взаимодействие осуществляется посредством электромагнитного поля — отдельным видом материи, пронизывающим всё пространство.
Электростатика
Основная статья: Электростатика
Электростатика рассматривает взаимодействие неподвижных заряженных тел. Основным законом электростатики является закон Кулона, устанавливающий связь между силой притяжения/отталкивания двух заряженных материальных точек, величиной их заряда и расстоянием между ними. В математической форме закон Кулона имеет вид[6]:
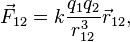
где 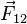 — сила, с которой частица 1 действует на частицу 2,
— сила, с которой частица 1 действует на частицу 2, 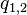 — величины зарядов частиц 1 и 2 соответственно,
— величины зарядов частиц 1 и 2 соответственно, 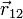 — радиус-вектор, проведённый из точки расположения частицы 1 в точку расположения частицы 2 (
— радиус-вектор, проведённый из точки расположения частицы 1 в точку расположения частицы 2 ( 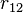 — модуль этого вектора),
— модуль этого вектора), 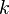 — размерный коэффициент, значение которого зависит от используемой системы единиц, в СГС он равен 1, в СИ:
— размерный коэффициент, значение которого зависит от используемой системы единиц, в СГС он равен 1, в СИ:
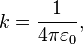
где 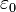 — электрическая постоянная.
— электрическая постоянная.
В рамках электростатики величина электрического поля, создаваемого точечным зарядом, определяется выражением[6]:
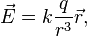
где 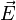 — напряжённость электрического поля в данной точке,
— напряжённость электрического поля в данной точке, 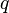 — величина заряда частицы, создающей это поле,
— величина заряда частицы, создающей это поле, 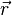 — радиус-вектор, проведённый из точки расположения частицы в точку, где определяется поле (
— радиус-вектор, проведённый из точки расположения частицы в точку, где определяется поле (  — модуль этого вектора).
— модуль этого вектора).
Сила, действующая на заряженную частицу, помещённую в электрическое поле, определяется выражением:
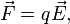
где 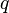 — величина электрического заряда частицы,
— величина электрического заряда частицы, 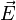 — векторная сумма напряжённостей электрических полей, созданных всеми частицами (за исключением рассматриваемой) в точке, где находится частица[6].
— векторная сумма напряжённостей электрических полей, созданных всеми частицами (за исключением рассматриваемой) в точке, где находится частица[6].
В случае, если заряд распределён в некотором объёме с плотностью 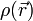 , то электростатическое поле, создаваемое им, может быть найдено из электростатической теоремы Гаусса, имеющей в дифференциальной форме в системе СГС следующий вид[7]:
, то электростатическое поле, создаваемое им, может быть найдено из электростатической теоремы Гаусса, имеющей в дифференциальной форме в системе СГС следующий вид[7]:
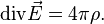
В присутствии поляризуемой диэлектрической среды величина электрического поля, создаваемого свободными зарядами, изменяется из-за влияния связанных зарядов, входящих в состав среды. Это изменение во многих случаях может быть охарактеризовано посредством введения вектора поляризации среды 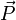 и вектора электрической индукции
и вектора электрической индукции 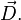 При этом выполняется следующее соотношение[8]:
При этом выполняется следующее соотношение[8]:
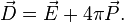
Теорема Гаусса в этом случае записывается в виде[8]:
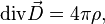
где под 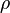 понимается плотность только свободных зарядов.
понимается плотность только свободных зарядов.
В большинстве случаев рассматриваемые поля значительно слабее внутриатомных полей, поэтому справедлива линейная связь между вектором поляризации и напряжённостью электрического поля в данной точке. Для изотропных сред математически этот факт выражается следующим равенством[9]:
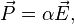
где 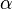 — коэффициент, характеризующий поляризуемость данного диэлектрика при данных температуре и давлении. Аналогично, справедлива линейная связь между напряжённостью и индукцией[9]:
— коэффициент, характеризующий поляризуемость данного диэлектрика при данных температуре и давлении. Аналогично, справедлива линейная связь между напряжённостью и индукцией[9]:
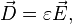
где коэффициент 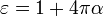 носит название диэлектрической проницаемости[9].
носит название диэлектрической проницаемости[9].
С учётом поляризуемой среды приведённые выше формулы для силы электростатического взаимодействия и напряжённости электростатического поля принимают вид[10]:
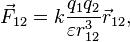
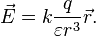
Магнитостатика
Основная статья: Магнитостатика
Магнитостатика изучает взаимодействие постоянных по величине и неподвижных в пространстве электрических токов, представляющих по своей сути поток заряженных частиц. В основе магнитостатики лежат закон Био — Савара — Лапласа и закон Ампера. Закон Био — Савара — Лапласа позволяет находить величину магнитного поля, создаваемого малым элементом тока. Если имеется линейный элемент тока длиною 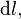 сила тока в котором равна
сила тока в котором равна 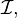 то он создаёт в окружающем пространстве магнитное поле, индукция которого определяется выражением[11]:
то он создаёт в окружающем пространстве магнитное поле, индукция которого определяется выражением[11]:
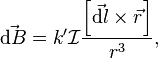
где 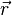 — радиус-вектор, проведённый от точки расположения элемента тока до точки пространства, в которой определяется магнитное поле (
— радиус-вектор, проведённый от точки расположения элемента тока до точки пространства, в которой определяется магнитное поле (  — модуль этого радиус-вектора),
— модуль этого радиус-вектора), 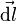 — вектор, длина которого равна
— вектор, длина которого равна 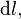 а направление совпадает с направлением тока
а направление совпадает с направлением тока 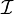 (считая, что направление тока определяется движением положительно заряженных частиц),
(считая, что направление тока определяется движением положительно заряженных частиц), 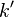 — константа, зависящая от выбора системы единиц: в системе СИ
— константа, зависящая от выбора системы единиц: в системе СИ 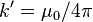 (
( 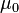 — магнитная постоянная), в системе СГС
— магнитная постоянная), в системе СГС 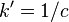 (
(  — скорость света в вакууме). Знаком × в квадратных скобках здесь и ниже обозначается векторное произведение.
— скорость света в вакууме). Знаком × в квадратных скобках здесь и ниже обозначается векторное произведение.
Закон Ампера определяет величину силы, с которой магнитное поле в данной точке действует на элемент тока[12]:
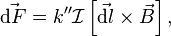
где 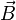 — величина магнитного поля в данной точке, равная векторной сумме магнитных полей, создаваемых всеми другими токами,
— величина магнитного поля в данной точке, равная векторной сумме магнитных полей, создаваемых всеми другими токами, 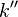 — коэффициент, зависящий от выбранной системы единиц: в системе СИ он равен единице, в системе СГС —
— коэффициент, зависящий от выбранной системы единиц: в системе СИ он равен единице, в системе СГС — 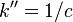 (
(  — скорость света в вакууме).
— скорость света в вакууме).
Закон Ампера является прямым следствием выражения для магнитной составляющей силы Лоренца — силы, с которой электромагнитное поле действует на заряженную частицу[13]:
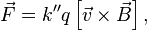
где 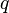 — заряд частицы,
— заряд частицы, 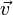 — её скорость.
— её скорость.
Закон Био — Савара — Лапласа может быть переписан в виде для плотности тока 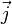 [14]:
[14]:
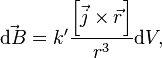
где 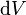 — объём элемента объёмного тока, создающего поле. Из этой формы закона Био — Савара — Лапласа можно вывести теорему о циркуляции магнитной индукции, которая в дифференциальной форме принимает вид[15]:
— объём элемента объёмного тока, создающего поле. Из этой формы закона Био — Савара — Лапласа можно вывести теорему о циркуляции магнитной индукции, которая в дифференциальной форме принимает вид[15]:
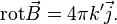
В присутствии магнитной среды (то есть среды, способной к намагничиванию) её влияние характеризуется векторами намагниченности среды 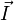 и напряжённости магнитного поля
и напряжённости магнитного поля 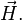 При этом справедлива связь:
При этом справедлива связь:
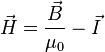 — в системе СИ[16],
— в системе СИ[16],
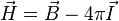 — в системе СГС[17].
— в системе СГС[17].
В линейных изотропных средах справедлива простая связь между величиной намагниченности и приложенным магнитным полем (физически более правильным было бы связывать намагниченность с величиной магнитной индукции, однако по историческим причинам её выражают обычно через напряжённость магнитного поля — ввиду линейной связи между величинами 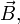
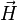 и
и 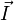 принципиального значения это не имеет)[18][19]:
принципиального значения это не имеет)[18][19]:
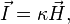
где коэффициент 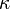 называется магнитной восприимчивостью среды. Часто оперируют также величиной магнитной проницаемости
называется магнитной восприимчивостью среды. Часто оперируют также величиной магнитной проницаемости 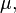 определяемой как:
определяемой как:
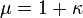 — в системе СИ[19],
— в системе СИ[19],
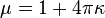 — в системе СГС[18].
— в системе СГС[18].
В этом случае справедливы соотношения:
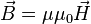 — в системе СИ[19],
— в системе СИ[19],
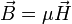 — в системе СГС[18].
— в системе СГС[18].
Следует отметить, что ферромагнетики являются принципиально нелинейными средами, в частности, они подвержены явлению гистерезиса, и поэтому простые соотношения, указанные выше, для них несправедливы.
Теорема о циркуляции в магнитных средах принимает следующий вид[17]:
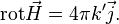
Дифференциальная форма[править | править исходный текст]
Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных[28]) линейным дифференциальным уравнениям в частных производных первого порядка для 12 компонент четырёх векторныхфункций ( 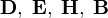 ):
):
| Название | СГС | СИ | Примерное словесное выражение |
| Закон Гаусса | 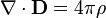 | 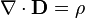 | Электрический заряд является источником электрической индукции. |
| Закон Гаусса для магнитного поля | 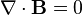 | 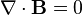 | Не существует магнитных зарядов.[~ 1] |
| Закон индукции Фарадея | 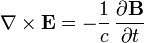 | 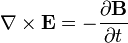 | Изменение магнитной индукции порождает вихревое электрическое поле.[~ 1] |
| Теорема о циркуляции магнитного поля | 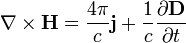 | 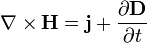 | Электрический ток и изменение электрической индукции порождают вихревое магнитное поле |
Жирным шрифтом в дальнейшем обозначаются векторные величины, курсивом — скалярные.
Введённые обозначения:
· 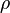 — плотность стороннего электрического заряда (в единицах СИ — Кл/м³);
— плотность стороннего электрического заряда (в единицах СИ — Кл/м³);
· 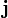 — плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как
— плотность электрического тока (плотность тока проводимости) (в единицах СИ — А/м²); в простейшем случае — случае тока, порождаемого одним типом носителей заряда, она выражается просто как 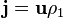 , где
, где 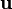 — (средняя) скорость движения этих носителей в окрестности данной точки,
— (средняя) скорость движения этих носителей в окрестности данной точки, 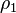 — плотность заряда этого типа носителей (она в общем случае не совпадает с
— плотность заряда этого типа носителей (она в общем случае не совпадает с 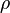 )[29]; в общем случае это выражение надо усреднить по разным типам носителей;
)[29]; в общем случае это выражение надо усреднить по разным типам носителей;
·  — скорость света в вакууме (299 792 458 м/с);
— скорость света в вакууме (299 792 458 м/с);
· 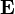 — напряжённость электрического поля (в единицах СИ — В/м);
— напряжённость электрического поля (в единицах СИ — В/м);
· 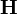 — напряжённость магнитного поля (в единицах СИ — А/м);
— напряжённость магнитного поля (в единицах СИ — А/м);
· 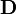 — электрическая индукция (в единицах СИ — Кл/м²);
— электрическая индукция (в единицах СИ — Кл/м²);
· 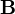 — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);
— магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);
·  — дифференциальный оператор набла, при этом:
— дифференциальный оператор набла, при этом:
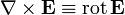 означает ротор вектора,
означает ротор вектора,
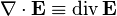 означает дивергенцию вектора.
означает дивергенцию вектора.
Приведённые выше уравнения Максвелла не составляют ещё полной системы уравнений электромагнитного поля, поскольку они не содержат свойств среды, в которой возбужденоэлектромагнитное поле. Соотношения, связывающие величины  ,
,  ,
, 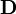 ,
, 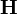 и
и 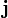 и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
и учитывающие индивидуальные свойства среды, называются материальными уравнениями.
Интегральная форма[править | править исходный текст]
При помощи формул Остроградского — Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:
| Название | СГС | СИ | Примерное словесное выражение |
| Закон Гаусса | 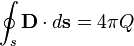 | 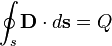 | Поток электрической индукции через замкнутую поверхность  пропорционален величине свободного заряда, находящегося в объёме пропорционален величине свободного заряда, находящегося в объёме 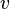 , который окружает поверхность , который окружает поверхность  . . |
| Закон Гаусса для магнитного поля | 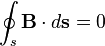 | 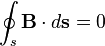 | Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют). |
| Закон индукции Фарадея | 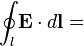 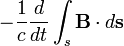 | 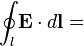 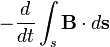 | Изменение потока магнитной индукции, проходящего через незамкнутую поверхность  , взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре , взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре 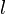 , который является границей поверхности , который является границей поверхности  . . |
| Теорема о циркуляции магнитного поля | 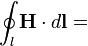 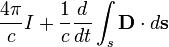 | 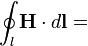 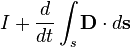 | Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность  , пропорциональны циркуляции магнитного поля на замкнутом контуре , пропорциональны циркуляции магнитного поля на замкнутом контуре 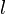 , который является границей поверхности , который является границей поверхности  . . |
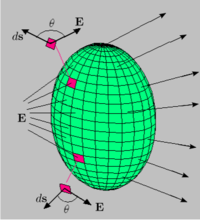

Поток электрического поля через замкнутую поверхность
Введённые обозначения:
·  — двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём
— двумерная замкнутая в случае теоремы Гаусса поверхность, ограничивающая объём 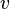 , и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур
, и открытая поверхность в случае законов Фарадея и Ампера — Максвелла (её границей является замкнутый контур 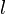 ).
).
· 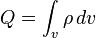 — электрический заряд, заключённый в объёме
— электрический заряд, заключённый в объёме 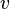 , ограниченном поверхностью
, ограниченном поверхностью  (в единицах СИ — Кл);
(в единицах СИ — Кл);
· 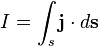 — электрический ток, проходящий через поверхность
— электрический ток, проходящий через поверхность  (в единицах СИ — А).
(в единицах СИ — А).
При интегрировании по замкнутой поверхности вектор элемента площади 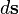 направлен из объёма наружу. Ориентация
направлен из объёма наружу. Ориентация 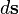 при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по
при интегрировании по незамкнутой поверхности определяется направлением правого винта, «вкручивающегося» при повороте в направлении обхода контурного интеграла по 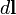 .
.
Словесное описание законов Максвелла, например, закона Фарадея, несёт отпечаток традиции, поскольку вначале при контролируемом изменении магнитного потока регистрировалось возникновение электрического поля (точнее электродвижущей силы). В общем случае в уравнениях Максвелла (как в дифференциальной, так и в интегральной форме) векторные функции 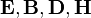 являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.
являются равноправными неизвестными величинами, определяемыми в результате решения уравнений.
Сила Лоренца[править | править исходный текст]
Основная статья: Сила Лоренца
При решении уравнений Максвелла распределения зарядов 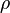 и токов
и токов 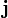 часто считаются заданными. С учётом граничных условий и материальных уравнений это позволяет определить напряжённость электрического поля
часто считаются заданными. С учётом граничных условий и материальных уравнений это позволяет определить напряжённость электрического поля 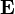 и магнитную индукцию
и магнитную индукцию 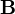 , которые, в свою очередь, определяют силу, действующую на пробный заряд
, которые, в свою очередь, определяют силу, действующую на пробный заряд 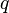 , двигающийся со скоростью
, двигающийся со скоростью 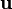 . Эта сила называется силой Лоренца:
. Эта сила называется силой Лоренца:
| СГС | СИ |
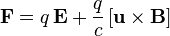 | 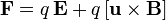 |
Электрическая составляющая силы направлена по электрическому полю (если 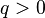 ), а магнитная — перпендикулярна скорости заряда и магнитной индукции. Впервые выражение для силы, действующей на заряд в магнитном поле (электрическая компонента была известна), получил в 1889 году Хевисайд[30][31] за три года до Хендрика Лоренца, который вывел выражение для этой силы в 1892 году.
), а магнитная — перпендикулярна скорости заряда и магнитной индукции. Впервые выражение для силы, действующей на заряд в магнитном поле (электрическая компонента была известна), получил в 1889 году Хевисайд[30][31] за три года до Хендрика Лоренца, который вывел выражение для этой силы в 1892 году.
В более сложных ситуациях в классической и квантовой физике в случае, когда под действием электромагнитных полей свободные заряды перемещаются и изменяют значения полей, необходимо решение самосогласованной системы из уравнений Максвелла и уравнений движения, включающих силы Лоренца. Получение точного аналитического решения такой полной системы сопряжено обычно с большими сложностями
История теории
Первоначально электричество и магнетизм считались двумя отдельными силами. Эта точка зрения изменилась, однако, с публикацией в 1873 году работы Джеймса Максвелла «Трактат по электричеству и магнетизму», в которой было показано, что взаимодействие положительных и отрицательных зарядов регулируется одной силой. Существуют четыре основных эффекта, следующие из этих взаимодействий, которые были ясно продемонстрированы экспериментами:
1. Электрические заряды притягиваются или отталкиваются друг от друга с силой, обратно пропорциональной квадрату расстояния между ними: разноимённые заряды притягиваются, одноимённые — отталкиваются.
2. Магнитные полюса (или состояния поляризации в отдельных точках) привлекают или отталкивают друг друга похожим способом и всегда идут парами: каждый северный полюс не существует отдельно от южного.
3. Электрический ток в проводе создает круговое магнитное поле вокруг провода, направленное (по или против часовой стрелки) в зависимости от течения тока.
4. Ток индуцируется в петле провода, когда он сдвигается ближе или дальше относительно магнитного поля или магнит перемещается ближе или дальше от петли провода; направление тока зависит от направления этих перемещений.
Готовясь к лекции, вечером 21 апреля 1820 года, Ганс Христиан Эрстед сделал удивительное наблюдение. Когда он занимался подборкой материала, то заметил, что стрелка компаса отклоняется от северного магнитного полюса, когда электрический ток от батареи, которую он использовал, включался и выключался. Это отклонение навело его на мысль, что магнитные поля исходят со всех сторон провода, по которому проходит электрический ток, подобно тому как распространяются в пространстве свет и тепло, и что опыт указывает на прямую связь между электричеством и магнетизмом.
На момент открытия, Эрстед не предложил удовлетворительного объяснения этого явления, и не пытался представить явление в математических выкладках. Однако, три месяца спустя, он стал проводить более интенсивные исследования. Вскоре после этого он опубликовал результаты своих исследований, доказав, что электрический ток создает магнитное поле, когда течёт по проводам. В системе СГС единицу электромагнитной индукции (Э) назвали в честь его вклада в область электромагнетизма.
Выводы, сделанные Эрстедом, привели к интенсивному исследованию электродинамики мировым научным сообществом. К 1820 году относятся также работы Доминика Франсуа Араго, который заметил, что проволока, по которой течет электрический ток, притягивает к себе железные опилки. Он же намагнитил впервые железные и стальные проволоки, помещая их внутрь катушки медных проволок, по которым проходил ток. Ему же удалось намагнитить иглу, поместив её в катушку и разрядивлейденскую банку через катушку. Независимо от Араго намагничивание стали и железа током было открыто Дэви. Первые количественные определения действия тока на магнит точно так же относятся к 1820 году и принадлежат французским учёнымЖан-Батисту Био и Феликсу Савару[20]. Опыты Эрстеда повлияли также на французского физика Андре-Мари Ампера, представившего электромагнитную закономерность между проводником и током в математической форме. Открытие Эрстеда также представляет собой важный шаг на пути к единой концепции поля.
Это единство, которое было обнаружено Майклом Фарадеем, дополнено Джеймсом Максвеллом, а также уточнено Оливером Хевисайдом и Генрихом Герцем, является одним из ключевых достижений XIX столетия в математической физике. У этого открытия были далеко идущие последствия, одним из которых стало понимание природы света. Свет и другие электромагнитные волны принимают форму квантованных самораспространяющихся колебательныхявлений электромагнитного поля, названных фотонами. Различные частоты колебания приводят к различным формам электромагнитного излучения: отрадиоволн на низких частотах, к видимому свету на средних частотах, к гамма-лучам на высоких частотах.
Эрстед не был единственным человеком, открывшим связь между электричеством и магнетизмом. В 1802 году Джованни Доменико Романьози, итальянский ученый-правовед, отклонял магнитную стрелку электростатическими разрядами. Но фактически в исследованиях Романьози не применялся гальванический элемент и постоянный ток как таковой отсутствовал. Отчёт об открытии были опубликован в 1802 году в итальянской газете, но он был почти не замечен научным сообществом того времени[21].
