Ыпуклость и вогнутость функций

Пусть функция 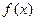дифференцируема на интервале 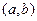. Тогда существует касательная к графику функции 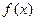в любой точке этого интервала.

Определение 3.График дифференцируемой функции 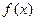называется выпуклым (вогнутым) на интервале 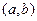, если он расположен на 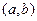ниже (выше) касательной, проведенной в любой его точке из 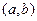(рис. 2).

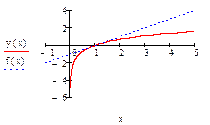
Рис.2

Теорема 5(достаточный признак выпуклости, вогнутости). Если функция 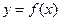имеет на интервале 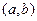вторую производную и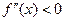 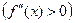во всех точках интервала 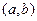, то график функции 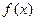– выпуклый (вогнутый).

Определение 4.Точка 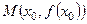называется точкой перегиба графика непрерывной функции 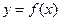, если точка 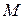разделяет промежутки, в которых график выпуклый и вогнутый.

Теорема 6(необходимое условие точки перегиба). Пусть график функции 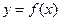имеет перегиб в точке 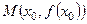и пусть функция 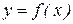имеет в окрестности точки 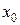непрерывную вторую производную. Тогда .

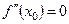Теорема 7 (достаточное условие точки перегиба). Пусть функция 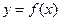имеет вторую производную в окрестности точки 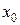. Если при переходе через точку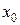 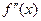меняет свой знак, то 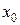- точка перегиба.

П р и м е р 3.Найти точки перегиба для функции .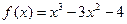

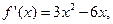
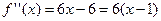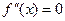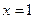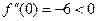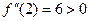Решение. , при . , . Следовательно, точка 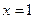– точка перегиба графика функции .

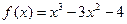симптоты графика функции

Определение 5. Прямая называется асимптотой графика функции 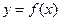, если расстояние от точки, принадлежащей графику до этой прямой, стремится к нулю при неограниченном удалении точки по графику функции от начала координат (рис. 3).

Рис. 3

Существует три типа асимптот: вертикальная, горизонтальная и наклонная.

Определение 6. Прямая 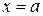называется вертикальной асимптотой графика функции 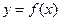, если хотя бы один из односторонних пределов функци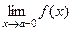и или 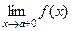равен 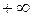или 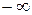(рис. 4).

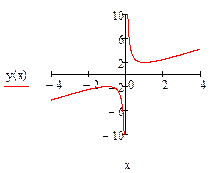
Рис. 4

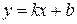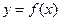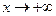Определение 7.Прямая называется наклонной асимптотой графика функции при (или 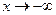), если .

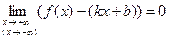Заметим, что при 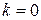наклонная асимптота часто называется горизонтальной.

Теорема 8. Прямая 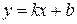является наклонной асимптотой к графику функции 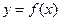, если существуют пределы 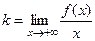, 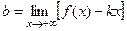. Если хотя бы один из этих двух пределов не существует или 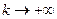( 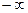), то кривая наклонных асимптот не имеет.

Задание 2. Найти асимптоты и построить график функции

.

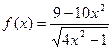Решение:

1) проверка функцию на четность.

Данная функция является четной, так как

.

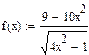
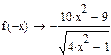
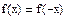2) найдем область определения функции.

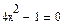
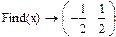
Область определения функции - .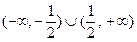

3) найдем вертикальные асимптоты

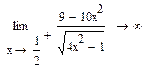
Следовательно, прямые 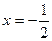и 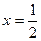являются вертикальными асимптотами.

4) найдем наклонные асимптоты

Так как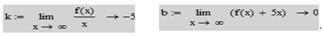

то 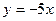является наклонной асимптотой н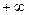а , а 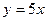- наклонная асимптота на .

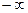4) найдем точки пересечения с осью Ox.

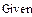
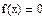
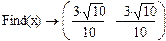
5) строим график функции.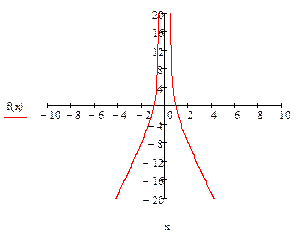

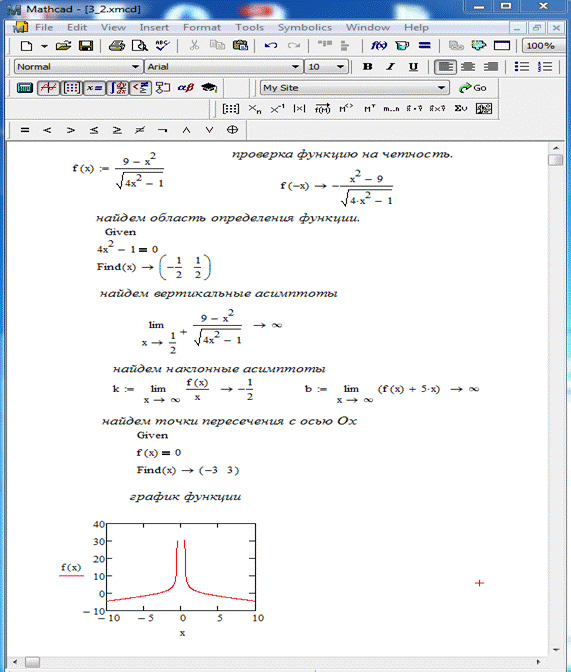
Рис. 5 – Выполнение задания 2

1.4. Схема исследования функции

1. Найти область определения функции, ее точки разрыва.

2. Найти точки пересечения с осями.

3. Выяснить является ли функция четной, нечетной или общего вида.

4. Найти интервалы монотонности и точки экстремума функции.

5. Найти интервалы выпуклости и вогнутости графика функции и точки перегиба.

6. Найти асимптоты графика функции.

7. На основании полученных результатов построить график функции.

Задание 3. Провести полное исследование функции 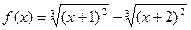и построить ее график.

Решение. Исследование выполним по предложенной схеме.

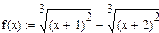
1) область определения функции: .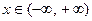

2) найдем точки пересечения графика функции с осями координат.

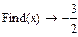
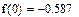
3) проверим, является ли функция четной, нечетной или общего вида.

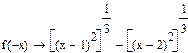
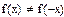
Функция общего вида.

4) найдем асимптоты графика функции (вертикальные, наклонные, горизонтальные).

Вертикальных асимптот нет, так как нет точек разрыва.

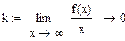
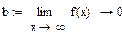
Прямая 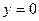является горизонтальной асимптотой на 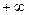и .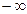

5) найдем промежутки монотонности (возрастания и убывания) функции и точки экстремума.

Находим производную первого порядка.

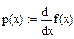
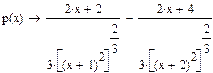
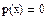
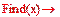
Производная не обращается в нуль, но не существует точках 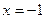и .

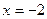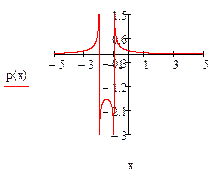
При переходе через точку 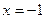производная 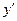меняет знак с «–» на «+», значит, 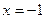– точка минимума функции. При переходе через точку 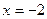производная 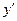меняет знак с «+» на «-», значит, 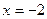– точка максимума функции.

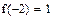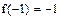Итак, функция возрастает на промежутках 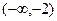и 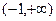, убывает на промежутке .

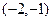6) найдем промежутки выпуклости и вогнутости графика функции и точки перегиба.

Для этого вычислим производную второго порядка и найдем критические точки.

;

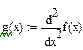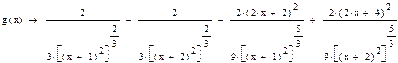
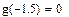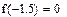, .Получили, что 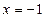, 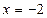и 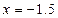- точки перегиба функции.

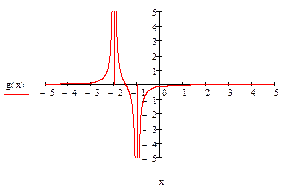
7) строим график данной функции.

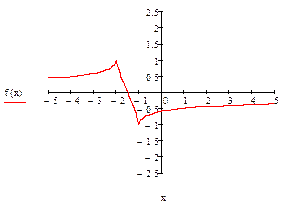
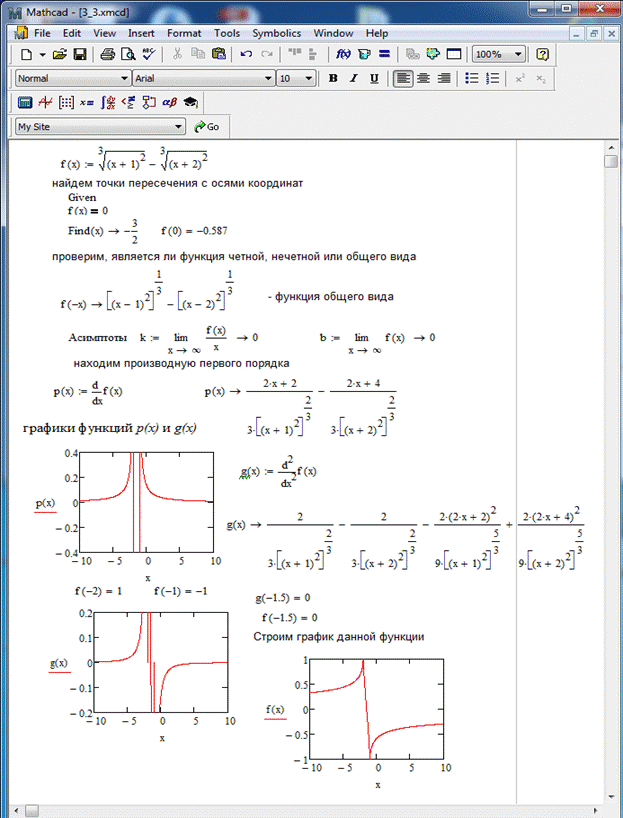
Рис.6 – Выполнение задания 3