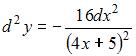Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное значение функции 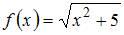 при
при 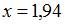 , вычисленное с использованием дифференциала первого порядка, равно …
, вычисленное с использованием дифференциала первого порядка, равно …
 | 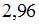 |
Тема: Дифференциальное исчисление ФНП
Значение частной производной 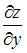 функции
функции 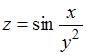 в точке
в точке 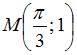 равно …
равно …
 | 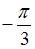 | ||
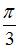 | |||
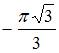 | |||
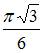 |
Решение:
При вычислении частной производной 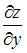 по переменной
по переменной 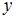 переменную
переменную 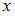 рассматриваем как постоянную величину. Тогда
рассматриваем как постоянную величину. Тогда
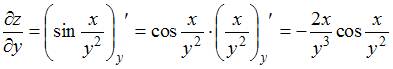 .
.
Следовательно, 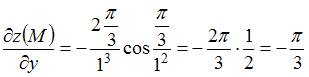
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
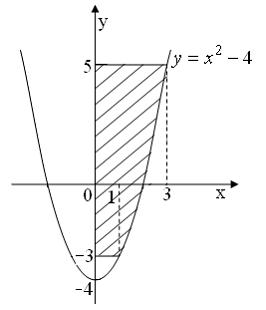
равна …
 | 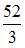 | ||
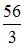 | |||
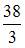 |
Решение:
Площадь данной фигуры можно вычислить по формуле 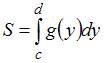 , где
, где 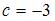
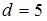
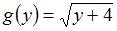 . Тогда
. Тогда 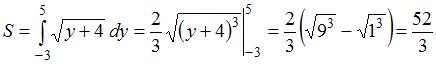
Тема: Непрерывность функции, точки разрыва
Для функции 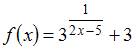 точка
точка 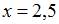 является точкой …
является точкой …
 | разрыва второго рода | ||
| разрыва первого рода | |||
| непрерывности | |||
| устранимого разрыва |
Решение:
Вычислим односторонние пределы функции 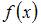 в точке
в точке 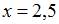 :
:
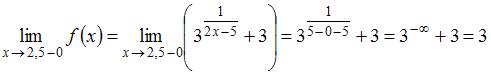 ,
,
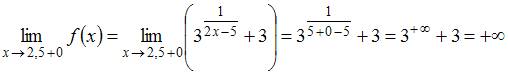 .
.
Так как один из односторонних пределов в точке 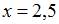 , а именно
, а именно 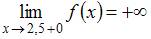 , то точка
, то точка 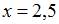 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дифференциал второго порядка функции 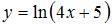 равен …
равен …
 | 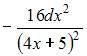 |
Тема: Дифференциальное исчисление ФНП
Частная производная второго порядка 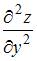 функции
функции 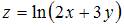 имеет вид …
имеет вид …
 | 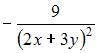 | ||
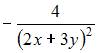 | |||
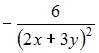 | |||
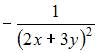 |
Решение:
При вычислении частной производной функции 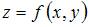 по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
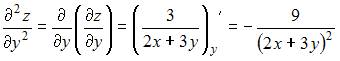 .
.
Тема: Непрерывность функции, точки разрыва
Для функции 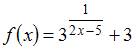 точка
точка 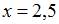 является точкой …
является точкой …
 | разрыва второго рода | ||
| разрыва первого рода | |||
| непрерывности | |||
| устранимого разрыва |
Решение:
Вычислим односторонние пределы функции 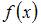 в точке
в точке 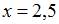 :
:
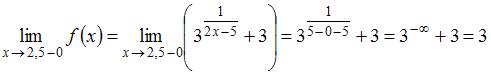 ,
,
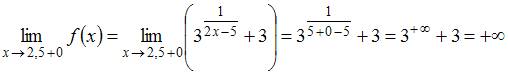 .
.
Так как один из односторонних пределов в точке 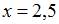 , а именно
, а именно 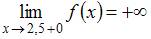 , то точка
, то точка 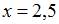 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
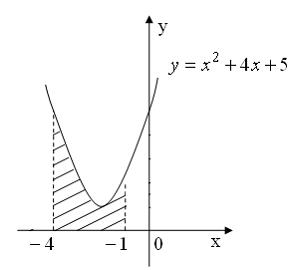
равна …
 | |||
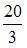 | |||
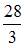 |
Решение:
Площадь данной фигуры можно вычислить по формуле 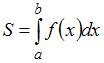 , где
, где 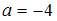 ,
, 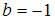 , а
, а 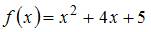 . Тогда
. Тогда
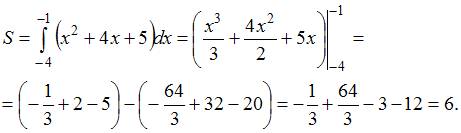
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дана функция 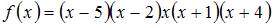 . Тогда больший действительный корень производной этой функции принадлежит промежутку …
. Тогда больший действительный корень производной этой функции принадлежит промежутку …
 | 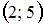 | ||
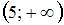 | |||
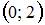 | |||
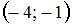 |
Решение:
Эта функция представляет собой полином пятого порядка и дифференцируема на всей числовой оси. Согласно теореме Ролля между двумя корнями (нулями) этой функции находится по крайней мере один корень ее производной. Поскольку 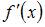 представляет собой полином (4-го порядка), то между двумя корнями функции
представляет собой полином (4-го порядка), то между двумя корнями функции 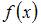 находится ровно один корень ее производной
находится ровно один корень ее производной 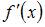 .
.
Найдем корни функции 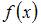 :
: 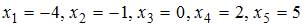 . Тогда больший действительный корень функции
. Тогда больший действительный корень функции 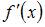 принадлежит интервалу
принадлежит интервалу 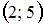
Тема: Дифференциальное исчисление ФНП
Частная производная 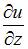 функции
функции 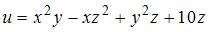 имеет вид …
имеет вид …
 | 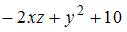 | ||
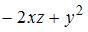 | |||
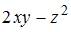 | |||
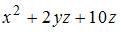 |
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дана функция 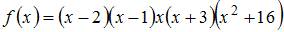 . Тогда меньший действительный корень производной этой функции принадлежит промежутку …
. Тогда меньший действительный корень производной этой функции принадлежит промежутку …
 | 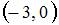 | ||
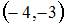 | |||
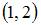 | |||
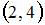 |
Решение:
Эта функция представляет собой полином 6-го порядка и дифференцируема на всей числовой оси. Согласно теореме Ролля между двумя корнями (нулями) этой функции находится по крайней мере один корень ее производной. Поскольку 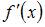 представляет собой полином (5-го порядка), то между двумя корнями функции
представляет собой полином (5-го порядка), то между двумя корнями функции 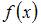 находится ровно один корень ее производной
находится ровно один корень ее производной 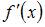 .
.
Найдем корни функции 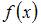 :
: 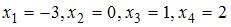 . Тогда меньший действительный корень функции
. Тогда меньший действительный корень функции 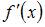 принадлежит интервалу
принадлежит интервалу 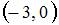 .
.
Тема: Непрерывность функции, точки разрыва
Точка разрыва функции 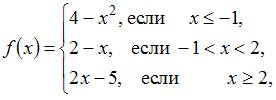 равна …2
равна …2
Тема: Приложения определенного интеграла
Площадь фигуры, ограниченной параболой 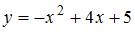 и осью
и осью 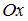 , равна …
, равна …
 | |||
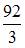 | |||
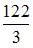 |
Решение:
Площадь данной фигуры можно вычислить по формуле 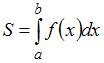 , где
, где 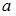 и
и 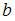 – это точки пересечения параболы и оси
– это точки пересечения параболы и оси 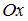 , а
, а 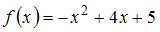 . Определим точки пересечения параболы и оси
. Определим точки пересечения параболы и оси 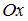 , решив уравнение
, решив уравнение 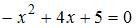 . Получаем:
. Получаем: 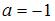 и
и 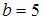 . Тогда
. Тогда
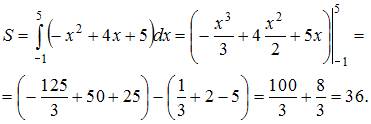
Тема: Дифференциальное исчисление ФНП
Полный дифференциал функции 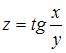 имеет вид …
имеет вид …
 | 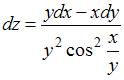 | ||
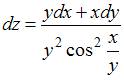 | |||
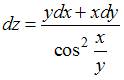 | |||
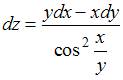 |
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть
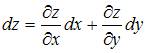 .
.
Тогда
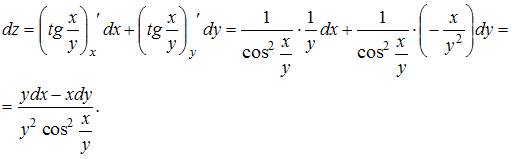
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Предел 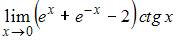 равен …
равен …
 | 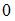 | ||
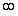 | |||
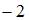 | |||
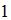 |
Решение:
Для вычисления данного предела применим правило Лопиталя. Так как 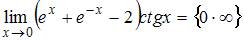 , то при помощи алгебраических преобразований получим неопределенность вида
, то при помощи алгебраических преобразований получим неопределенность вида 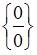 , или
, или 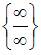 , например:
, например:
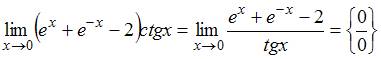 .
.
Тогда можно воспользоваться формулой вида 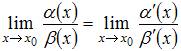 , то есть
, то есть 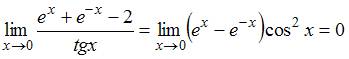 .
.
Тема: Непрерывность функции, точки разрыва
Точка разрыва функции 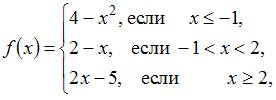 равна …
равна …
 | |||
| – 1 | |||
Решение:
Данная функция определена и непрерывна на каждом из интервалов 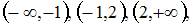 и меняет свое аналитическое выражение в точках
и меняет свое аналитическое выражение в точках 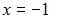 и
и 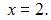 Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Для точки 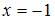 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
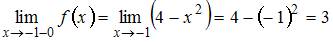 ,
,
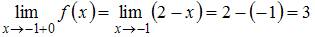 , и
, и 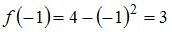 .
.
Так как 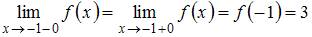 , то точка
, то точка 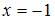 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.
Для точки 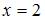 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
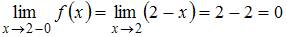 ,
,
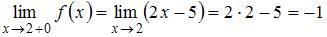 , и
, и 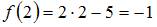 .
.
Так как 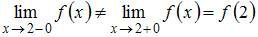 , то точка
, то точка 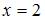 является точкой разрыва первого рода.
является точкой разрыва первого рода.
Тема: Непрерывность функции, точки разрыва
Для функции 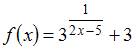 точка
точка 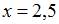 является точкой …
является точкой …
 | разрыва второго рода | ||
| разрыва первого рода | |||
| непрерывности | |||
| устранимого разрыва |
Решение:
Вычислим односторонние пределы функции 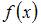 в точке
в точке 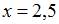 :
:
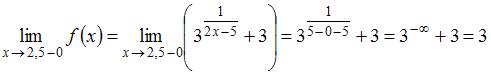 ,
,
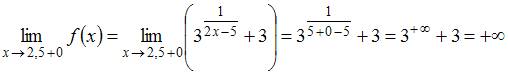 .
.
Так как один из односторонних пределов в точке 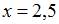 , а именно
, а именно 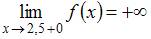 , то точка
, то точка 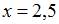 является точкой разрыва второго рода.
является точкой разрыва второго рода.
Тема: Приложения определенного интеграла
Длина дуги кривой 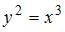 от точки
от точки 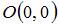 до точки
до точки 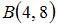 равна …
равна …
 | 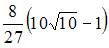 | ||
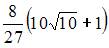 | |||
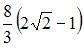 | |||
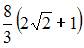 |
Решение:
Длина дуги плоской кривой 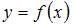 , ограниченной прямыми
, ограниченной прямыми 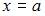 ,
, 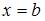 , определяется по формуле
, определяется по формуле 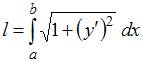 . В нашем случае
. В нашем случае 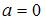 ,
, 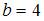 , а
, а 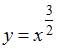 .
.
Тогда
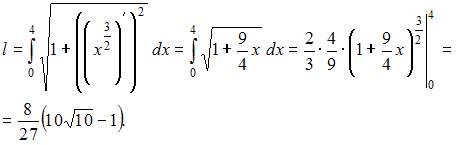
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное значение функции 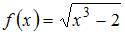 при
при 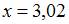 , вычисленное с использованием дифференциала первого порядка, равно …
, вычисленное с использованием дифференциала первого порядка, равно …
 | 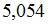 | ||
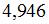 | |||
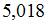 | |||
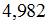 |
Решение:
Воспользуемся приближенной формулой:
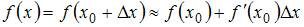 .
.
Полагая 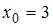 ,
, 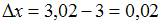 , приходим к равенству
, приходим к равенству
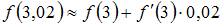 .
.
Вычислив последовательно
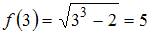 ,
,
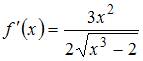 и
и 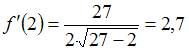 , получаем:
, получаем:
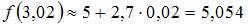 .
.
Тема: Дифференциальное исчисление ФНП
Смешанная частная производная второго порядка 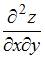 функции
функции 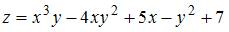 имеет вид …
имеет вид … 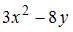
Тема: Дифференциальное исчисление ФНП
Полный дифференциал функции 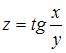 имеет вид …
имеет вид …
 | 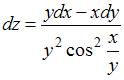 | ||
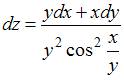 | |||
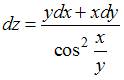 | |||
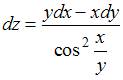 |
Решение:
Полный дифференциал функции нескольких переменных равен сумме произведений частных производных этой функции на дифференциалы соответствующих независимых переменных, то есть
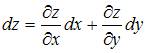 .
.
Тогда
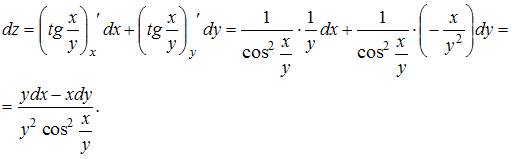
Тема: Непрерывность функции, точки разрыва
Точка разрыва функции 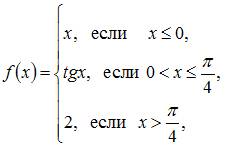 равна …
равна …
 | 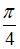 | ||
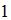 | |||
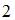 | |||
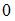 |
Решение:
Данная функция определена и непрерывна на каждом из интервалов 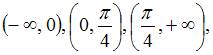 и меняет свое аналитическое выражение в точках
и меняет свое аналитическое выражение в точках 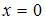 и
и 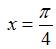 . Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
. Поэтому функция может иметь разрыв только в этих точках. Исследуем их на непрерывность.
Для точки 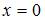 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
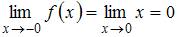 ,
,
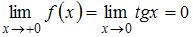 , и
, и 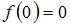 .
.
Так как 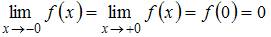 , то точка
, то точка 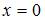 является точкой непрерывности данной функции.
является точкой непрерывности данной функции.
Для точки 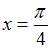 вычислим односторонние пределы и значение функции в этой точке:
вычислим односторонние пределы и значение функции в этой точке:
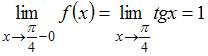 ,
,
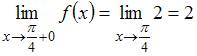 , и
, и 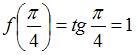 .
.
Так как 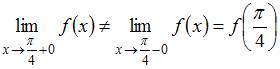 , то точка
, то точка 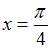 является точкой разрыва первого рода.
является точкой разрыва первого рода.
Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке
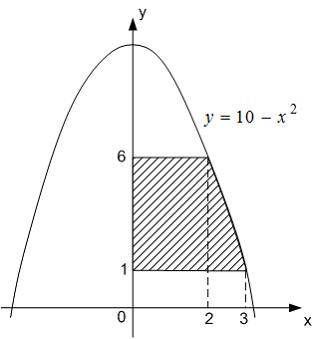
равна …
 | 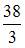 | ||
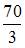 | |||
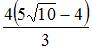 | |||
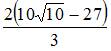 |
Решение:
Площадь данной фигуры можно вычислить по формуле 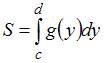 , где
, где 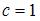 ,
, 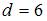 ,
, 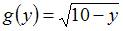 . Тогда
. Тогда
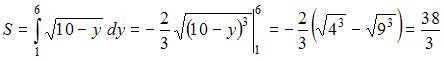 .
.
Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дифференциал второго порядка функции 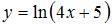 равен …
равен …
 | 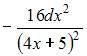 | ||
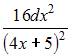 | |||
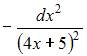 | |||
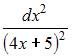 |
Решение:
Дифференциал второго порядка 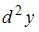 функции
функции 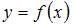 выражается формулой
выражается формулой 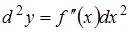 . Тогда, вычислив
. Тогда, вычислив 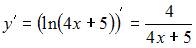 и
и 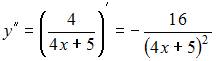 , получаем, что
, получаем, что